Floor Computer Science . The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. The floor of a real number is just the largest integer that is smaller than or equal to the number. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. That is, given x x the floor ⌊x⌋ ⌊ x. For example, ceil value of 3.883 is 3. It rounds down a given. The modern notation is $\lfloor.
from lib.unb.ca
\mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The modern notation is $\lfloor. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. For example, ceil value of 3.883 is 3. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. The floor of a real number is just the largest integer that is smaller than or equal to the number. That is, given x x the floor ⌊x⌋ ⌊ x. It rounds down a given.
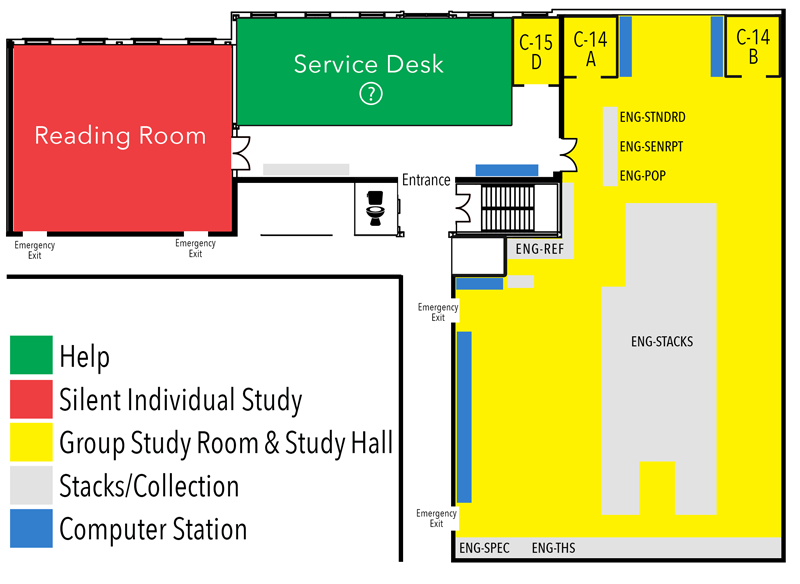
Floor Plan Engineering & Computer Science Library
Floor Computer Science The modern notation is $\lfloor. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The floor of a real number is just the largest integer that is smaller than or equal to the number. It rounds down a given. That is, given x x the floor ⌊x⌋ ⌊ x. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The modern notation is $\lfloor. For example, ceil value of 3.883 is 3. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value.
From www.youtube.com
How to build a computer lab with 2D design step by step YouTube Floor Computer Science The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. Floor function is used in. Floor Computer Science.
From www.reddit.com
Circuit Board Floor Science Building, UVU) r/ArchitecturePorn Floor Computer Science For example, ceil value of 3.883 is 3. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. That is, given x x the floor ⌊x⌋ ⌊ x. The floor(x) function in c. Floor Computer Science.
From www.bu.edu
BU’s Center for Computing & Data Sciences is Taking Shape BU Today Floor Computer Science For example, ceil value of 3.883 is 3. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). It rounds. Floor Computer Science.
From www.pinterest.com
EEE, IT, ECE and computer science college departments floor plan Floor Computer Science The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. That is, given x x the floor ⌊x⌋ ⌊ x. For example, ceil value of 3.883 is 3. Floor function is used in situations where exact integer values. Floor Computer Science.
From selectechlabfloors.com
Checklist for Replacing Your Laboratory Flooring Laboratory Flooring Floor Computer Science The modern notation is $\lfloor. For example, ceil value of 3.883 is 3. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The floor of a real number is just the largest integer that is smaller than or equal to. Floor Computer Science.
From www.bu.edu
Center for Computing & Data Sciences Building Boston University Floor Computer Science In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. The floor of a real number is just the largest integer that is smaller than or equal to the number. That is, given x x the floor ⌊x⌋ ⌊ x. The function of a real variable that assigns to a real. Floor Computer Science.
From www.hamiltonflooring.co.uk
Best Flooring for Laboratories and Science Rooms Hamilton Flooring Floor Computer Science That is, given x x the floor ⌊x⌋ ⌊ x. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor of a real number is just the largest integer that is smaller than or equal to the number. The function of a real variable that. Floor Computer Science.
From www.fullerton.edu
SGC 4th Floor Division of Information Technology CSUF Floor Computer Science The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. In. Floor Computer Science.
From viewfloor.co
Floor Plan Computer Lab Design Layout Viewfloor.co Floor Computer Science For example, ceil value of 3.883 is 3. The modern notation is $\lfloor. That is, given x x the floor ⌊x⌋ ⌊ x. The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. It rounds down. Floor Computer Science.
From www.raisedfloor.co.uk
Raised Access Flooring A Guide Floor Computer Science Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. For example, ceil value of 3.883 is 3. \mathbb{r} \to \mathbb{z}\) of a real number \(x\). Floor Computer Science.
From www.archdaily.com
Gallery of KPMB Architects Designs Stacked Data Sciences Tower for Floor Computer Science The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The floor of a real number is just the largest integer that is smaller than or equal to the number. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The floor function, denoted as floor(x) or ⌊x⌋, returns the largest. Floor Computer Science.
From success.fullerton.edu
Pollak Library Technology Student Success Initiative CSUF Floor Computer Science For example, ceil value of 3.883 is 3. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. That is, given x x the floor ⌊x⌋ ⌊ x. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. The function. Floor Computer Science.
From www.education.edu
Computer Lab Room 202 Roanoke Higher Education Center Roanoke Floor Computer Science That is, given x x the floor ⌊x⌋ ⌊ x. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The floor function (also known as the greatest integer. Floor Computer Science.
From lernerhall.columbia.edu
Computer Labs Alfred J. Lerner Hall Floor Computer Science The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. The modern notation is $\lfloor. That is, given x x the floor ⌊x⌋ ⌊ x. For example, ceil value of. Floor Computer Science.
From www.education.edu
Computer Lab Room 202 Roanoke Higher Education Center Roanoke Floor Computer Science Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The floor(x) function in c is used to compute the largest integer value less than or equal to a. Floor Computer Science.
From www.amtekcompany.com
Lab Design and Layout Floor Computer Science The modern notation is $\lfloor. The floor of a real number is just the largest integer that is smaller than or equal to the number. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The. Floor Computer Science.
From www.labkafe.com
Lab Flooring Explained Types of Laboratory Floorings and Pros & Cons Floor Computer Science Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The modern notation is $\lfloor. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. The function of a real variable that assigns to a real number $x$. Floor Computer Science.
From continuingeducation.bnpmedia.com
CE Center Flooring for Laboratory Designs Floor Computer Science The floor of a real number is just the largest integer that is smaller than or equal to the number. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. It rounds down. Floor Computer Science.
From lib.unb.ca
Floor Plan Engineering & Computer Science Library Floor Computer Science The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The floor of a real number is just the largest integer that is smaller than or equal to the number. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. \mathbb{r} \to \mathbb{z}\). Floor Computer Science.
From www.flickr.com
1st Floor Computer Lab Southern Utah University, Sherrat… Flickr Floor Computer Science The floor of a real number is just the largest integer that is smaller than or equal to the number. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to. Floor Computer Science.
From www.parterreflooring.com
The Benefits of Using Luxury Vinyl for Lab Flooring Floor Computer Science Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor of a real number is just the largest integer that is smaller than or equal to the number. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to. Floor Computer Science.
From www.researchgate.net
Skyline College Makerspace (Fab Lab) Layout Download Scientific Diagram Floor Computer Science It rounds down a given. The modern notation is $\lfloor. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor function (also known as the greatest. Floor Computer Science.
From library.ryerson.ca
New Computers in Commons Learning Lab Toronto Metropolitan University Floor Computer Science The floor of a real number is just the largest integer that is smaller than or equal to the number. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. It. Floor Computer Science.
From blogs.adams.edu
Second Floor Computer Lab Library News and Events Floor Computer Science The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. That is, given x x the floor ⌊x⌋ ⌊ x. For example,. Floor Computer Science.
From www.nersc.gov
Berkeley Lab’s New Computing Sciences Facility Features FirstofIts Floor Computer Science Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: In mathematics and computer science, the floor() and. Floor Computer Science.
From chicagoyimby.com
Foundation Work Continues for UIC's Computer Design Research and Floor Computer Science It rounds down a given. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than. Floor Computer Science.
From www.researchgate.net
Floor plans of Building 3, 1st floor with computer laboratory, 2nd Floor Computer Science In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. For example, ceil value of 3.883 is 3. It rounds down a given. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the. Floor Computer Science.
From www.silikalamerica.com
Laboratory Flooring Floors for Laboratories Silikal Floor Computer Science It rounds down a given. That is, given x x the floor ⌊x⌋ ⌊ x. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. For example, ceil value of 3.883 is 3. The. Floor Computer Science.
From floorplans.click
Lab Floor Plan Design floorplans.click Floor Computer Science The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The floor of a real number is just the largest integer that is smaller than or equal to the number. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. That is, given x x the floor ⌊x⌋ ⌊ x. In. Floor Computer Science.
From www.edrawmax.com
Basic Computer Laboratory floor plan EdrawMax Templates Floor Computer Science It rounds down a given. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The modern notation is $\lfloor. The floor of a real number is just the largest integer that is smaller than or equal to the number. That is, given x x the floor ⌊x⌋ ⌊ x. For example,. Floor Computer Science.
From www.pinterest.com
Computer Lab Layout 2 디자인, 인테리어, 도서관 디자인 Floor Computer Science The floor of a real number is just the largest integer that is smaller than or equal to the number. The floor function, denoted as floor(x) or ⌊x⌋, returns the largest integer less than or equal to x. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. The. Floor Computer Science.
From www.pinterest.com
Learning Floor Computer Science In mathematics and computer science, the floor() and ceil() functions that are defined in header file, map a real. The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. It rounds down a given. The floor function (also known as the greatest integer function) \(\lfloor\cdot\rfloor: The floor of a. Floor Computer Science.
From www.scranton.edu
Computing Sciences Robotics Lab Floor Computer Science Floor function is used in situations where exact integer values are required which is just lesser than or equal to the given value. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The. Floor Computer Science.
From www.library.wisc.edu
Computer Lab College Library UWMadison Libraries Floor Computer Science That is, given x x the floor ⌊x⌋ ⌊ x. For example, ceil value of 3.883 is 3. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The modern notation is $\lfloor. The function of a real variable that assigns to a real number $x$ the largest integer $\leq x$. The. Floor Computer Science.
From www.bu.edu
Center for Computing & Data Sciences Building Gallery Boston University Floor Computer Science The modern notation is $\lfloor. \mathbb{r} \to \mathbb{z}\) of a real number \(x\) denotes the greatest integer less than or equal to \(x\). The floor(x) function in c is used to compute the largest integer value less than or equal to a given number. Floor function is used in situations where exact integer values are required which is just lesser. Floor Computer Science.