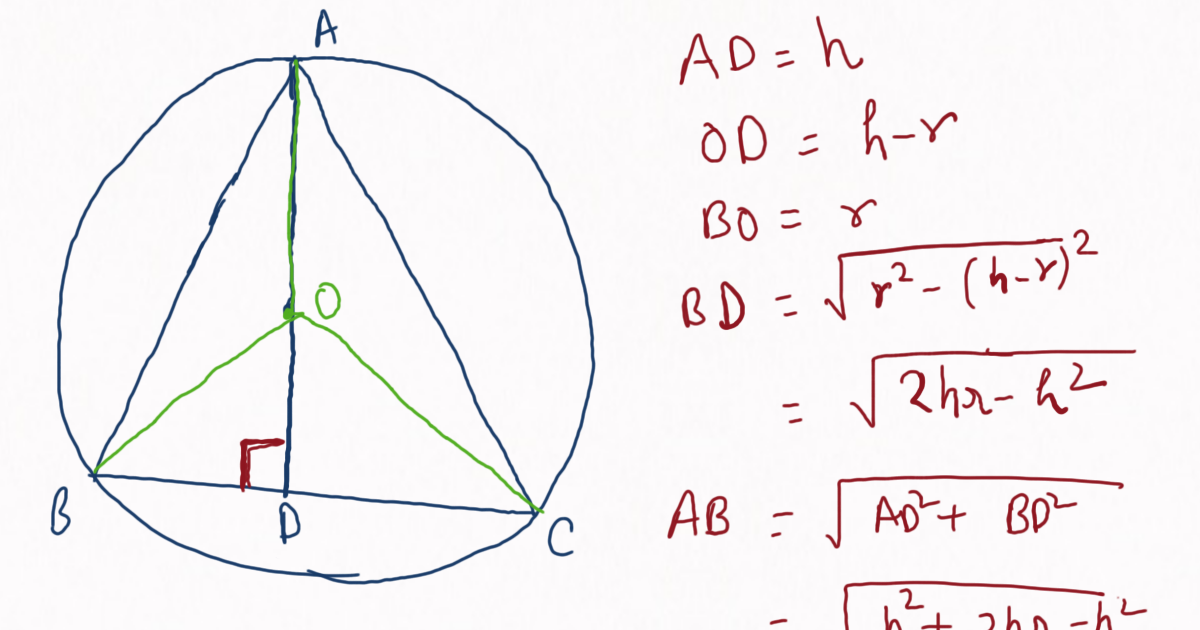
Isosceles Triangle Inscribed In A Circle . Show that triangles cob and coa are both isosceles triangles. Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. In a triangle abc a b c, ac = bc = 24 a c = b c = 24 and a circle with center j j is inscribed. Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. An isosceles triangle is inscribed in a circle. A b c o 32° 74° 74° solution first, to determine the. This common ratio has a geometric meaning: Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. A circle is inscribed in an isosceles with the given dimensions. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. Draw height bk in it. By dropping a perpendicular from the top of. Find the radius of the circle. It is the diameter (i.e. Let a circle with radius r be inscribed into this triangle.
from www.updateans.com
A circle is inscribed in an isosceles with the given dimensions. It is the diameter (i.e. This common ratio has a geometric meaning: Let a circle with radius r be inscribed into this triangle. Draw height bk in it. Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Express the inscribed circle’s radius in terms of the base ac and the height. If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle.
Update ANS ABC is an isosceles triangle inscribed in a circle of
Isosceles Triangle Inscribed In A Circle Show that triangles cob and coa are both isosceles triangles. An isosceles triangle is inscribed in a circle. A b c o 32° 74° 74° solution first, to determine the. By dropping a perpendicular from the top of. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Find the radius of the circle. In a triangle abc a b c, ac = bc = 24 a c = b c = 24 and a circle with center j j is inscribed. Express the inscribed circle’s radius in terms of the base ac and the height. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. Let a circle with radius r be inscribed into this triangle. Consider isosceles triangle abc (ав=вс). Find the angles in the three minor segments of the circle cut off by the sides of this triangle. Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. This common ratio has a geometric meaning: Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. Draw height bk in it.
From www.numerade.com
SOLVED In the given figure, triangle ABC is an isosceles triangle Isosceles Triangle Inscribed In A Circle A circle is inscribed in an isosceles with the given dimensions. Find the radius of the circle. This common ratio has a geometric meaning: By dropping a perpendicular from the top of. In a triangle abc a b c, ac = bc = 24 a c = b c = 24 and a circle with center j j is inscribed.. Isosceles Triangle Inscribed In A Circle.
From frojeostern.com
Show that the isosceles triangle of maximum area inscribed in a given Isosceles Triangle Inscribed In A Circle Find the radius of the circle. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. Twice the radius) of the unique circle. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
Maximum Area of Isosceles Triangle Inscribed in a Circle Calculus YouTube Isosceles Triangle Inscribed In A Circle In a triangle abc a b c, ac = bc = 24 a c = b c = 24 and a circle with center j j is inscribed. Let a circle with radius r be inscribed into this triangle. Draw height bk in it. A b c o 32° 74° 74° solution first, to determine the. Solution since the triangle’s. Isosceles Triangle Inscribed In A Circle.
From www.bartleby.com
Answered Find the area of the largest isosceles… bartleby Isosceles Triangle Inscribed In A Circle If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: It is the diameter (i.e. Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. This common ratio has a geometric meaning: An isosceles triangle is inscribed in a circle. Draw height. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
Problem Isosceles Triangle Inscribed in a Circle YouTube Isosceles Triangle Inscribed In A Circle It is the diameter (i.e. Find the radius of the circle. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. In a triangle abc a b c, ac = bc = 24 a c = b c. Isosceles Triangle Inscribed In A Circle.
From www.math-principles.com
Math Principles Proving Inscribed Triangle, Circle Isosceles Triangle Inscribed In A Circle Draw height bk in it. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. In a triangle abc. Isosceles Triangle Inscribed In A Circle.
From ar.inspiredpencil.com
Inscribed Triangle Isosceles Triangle Inscribed In A Circle Let a circle with radius r be inscribed into this triangle. Find the radius of the circle. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. This common ratio has a geometric meaning: Consider isosceles triangle abc (ав=вс). If ch c h is altitude (ch ⊥ ab, h ∈ ab). Isosceles Triangle Inscribed In A Circle.
From www.vrogue.co
Area Of Triangle And Circle vrogue.co Isosceles Triangle Inscribed In A Circle A circle is inscribed in an isosceles with the given dimensions. By dropping a perpendicular from the top of. Find the radius of the circle. Let a circle with radius r be inscribed into this triangle. An isosceles triangle is inscribed in a circle. It is the diameter (i.e. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c. Isosceles Triangle Inscribed In A Circle.
From www.updateans.com
Update ANS ABC is an isosceles triangle inscribed in a circle of Isosceles Triangle Inscribed In A Circle Consider isosceles triangle abc (ав=вс). Draw height bk in it. In a triangle abc a b c, ac = bc = 24 a c = b c = 24 and a circle with center j j is inscribed. Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. Find the radius of the circle. If. Isosceles Triangle Inscribed In A Circle.
From quizlet.com
Consider an isosceles triangle inscribed in a circle of radi Quizlet Isosceles Triangle Inscribed In A Circle A circle is inscribed in an isosceles with the given dimensions. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. Find the radius of the circle. Let a circle with radius r be inscribed into this triangle. This common ratio has a geometric meaning: A b c o 32° 74°. Isosceles Triangle Inscribed In A Circle.
From mathinschool.com
Derivation of Formula for Radius of Circle inscribed in Triangle Isosceles Triangle Inscribed In A Circle Show that triangles cob and coa are both isosceles triangles. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. It is the diameter (i.e. By dropping a perpendicular from the top of. A b c o 32°. Isosceles Triangle Inscribed In A Circle.
From www.vrogue.co
Formulas Radius Of Inscribed And Circumscribed Circle vrogue.co Isosceles Triangle Inscribed In A Circle Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. A. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
Putnam math contest A rectangle & isosceles triangle inscribed in a Isosceles Triangle Inscribed In A Circle Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. A circle is inscribed in an isosceles with the given dimensions. Find the radius of the circle. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. Express the inscribed circle’s radius in terms of the. Isosceles Triangle Inscribed In A Circle.
From www.topperlearning.com
ABC is an isosceles triangle inscribed in a circle.If AB=AC=12√5cm and Isosceles Triangle Inscribed In A Circle It is the diameter (i.e. Consider isosceles triangle abc (ав=вс). Show that triangles cob and coa are both isosceles triangles. By dropping a perpendicular from the top of. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: In a triangle abc a. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
Find max area of isosceles triangle inscribed in circle of radius 14 Isosceles Triangle Inscribed In A Circle Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. A circle is inscribed in an isosceles with the given dimensions. Consider isosceles triangle abc (ав=вс). An isosceles triangle is inscribed in a circle. If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b). Isosceles Triangle Inscribed In A Circle.
From www.chegg.com
Solved For the isosceles triangle inscribed in a circle of Isosceles Triangle Inscribed In A Circle If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: It is the diameter (i.e. Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. This common ratio has a geometric meaning: Solution since the triangle’s base is the circle’s diameter, the. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
Finding the Radius of an Inscribed Circle in a Triangle YouTube Isosceles Triangle Inscribed In A Circle Draw height bk in it. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Find the radius of the circle. In a triangle. Isosceles Triangle Inscribed In A Circle.
From quizlet.com
Triangle BCD is isosceles and BC ≅ BD. What is the measure o Quizlet Isosceles Triangle Inscribed In A Circle Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. An isosceles triangle is inscribed in a circle. In a triangle abc a b c, ac = bc = 24 a c = b c = 24 and a circle with center j j is inscribed. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle. Isosceles Triangle Inscribed In A Circle.
From www.vrogue.co
Formulas Radius Of Inscribed And Circumscribed Circle vrogue.co Isosceles Triangle Inscribed In A Circle Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. Draw height bk in it. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. This common ratio has a geometric meaning: By. Isosceles Triangle Inscribed In A Circle.
From brainly.in
pqr is an isosceles triangle inscribed in a circle if PQ equal to PR Isosceles Triangle Inscribed In A Circle Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. Consider isosceles triangle abc (ав=вс). If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: Find the angles in the three minor segments of the circle cut off by the sides of. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
Circle Theorems Isosceles Triangle in Circles (Grade 6) OnMaths GCSE Isosceles Triangle Inscribed In A Circle Find the radius of the circle. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Consider isosceles triangle abc (ав=вс). It is the diameter (i.e. If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b,. Isosceles Triangle Inscribed In A Circle.
From byjus.com
55. Isosceles triangle ABC is inscribed in a circle. If AB=AC =25cm Isosceles Triangle Inscribed In A Circle By dropping a perpendicular from the top of. Show that triangles cob and coa are both isosceles triangles. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. Draw height bk in it. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of. Isosceles Triangle Inscribed In A Circle.
From socratic.org
A triangle has corners at (4 , 5 ), (3 ,2 ), and (1 ,3 ). What is the Isosceles Triangle Inscribed In A Circle Show that triangles cob and coa are both isosceles triangles. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Consider isosceles triangle abc (ав=вс). If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h. Isosceles Triangle Inscribed In A Circle.
From www.geogebra.org
Optimized Circle Inscribed in an Isosceles Triangles GeoGebra Isosceles Triangle Inscribed In A Circle Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. Find the angles in the three minor segments of the circle cut off by the sides of this triangle. In a triangle abc a b c, ac = bc = 24 a c = b c = 24 and a circle with center j j. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
National 5 Mathematics Isosceles Triangles in Circles YouTube Isosceles Triangle Inscribed In A Circle Show that triangles cob and coa are both isosceles triangles. A b c o 32° 74° 74° solution first, to determine the. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Given an isosceles triangle inscribed in a circle with a radius. Isosceles Triangle Inscribed In A Circle.
From www.meritnation.com
ABC is an isosceles triangle inscribed in a circle with radius 9 CM Isosceles Triangle Inscribed In A Circle An isosceles triangle is inscribed in a circle. Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. A circle is inscribed in an isosceles with the given dimensions. If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: Draw height bk. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
Find the value of radius, when an isosceles triangle is inscribed in Isosceles Triangle Inscribed In A Circle Draw height bk in it. Express the inscribed circle’s radius in terms of the base ac and the height. This common ratio has a geometric meaning: Find the radius of the circle. Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. Find the angles in the three minor segments of the circle cut off. Isosceles Triangle Inscribed In A Circle.
From www.youtube.com
If an isosceles triangle ABC in which AB=AC=6cm, is inscribed in a Isosceles Triangle Inscribed In A Circle If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: Consider isosceles triangle abc (ав=вс). It is the diameter (i.e. Find the radius of the circle. Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. Find the angles in the three. Isosceles Triangle Inscribed In A Circle.
From www.math-principles.com
Math Principles Proving Inscribed Triangle, Circle Isosceles Triangle Inscribed In A Circle Express the inscribed circle’s radius in terms of the base ac and the height. Twice the radius) of the unique circle in which \(\triangle\,abc\) can be inscribed, called the. A b c o 32° 74° 74° solution first, to determine the. Find the radius of the circle. Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a. Isosceles Triangle Inscribed In A Circle.
From byjus.com
An equilateral triangle ABC is inscribed in a circle of radius 12 cm Isosceles Triangle Inscribed In A Circle Consider isosceles triangle abc (ав=вс). An isosceles triangle is inscribed in a circle. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. In a triangle abc a b c, ac = bc = 24 a c =. Isosceles Triangle Inscribed In A Circle.
From byjus.com
In the given figure, an isosceles triangle ABC, with AB = AC Isosceles Triangle Inscribed In A Circle Solution since the triangle’s base is the circle’s diameter, the triangle is a right triangle. A b c o 32° 74° 74° solution first, to determine the. A circle is inscribed in an isosceles with the given dimensions. This common ratio has a geometric meaning: If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥. Isosceles Triangle Inscribed In A Circle.
From www.meritnation.com
Prove that the least perimeter of an Isosceles Triangle in which a Isosceles Triangle Inscribed In A Circle A b c o 32° 74° 74° solution first, to determine the. Given an isosceles triangle inscribed in a circle with a radius of 5 cm and the base of the triangle being a diameter of the circle, find the area of the triangle. Draw height bk in it. If ch c h is altitude (ch ⊥ ab, h ∈. Isosceles Triangle Inscribed In A Circle.
From www.toppr.com
Prove that the least perimeter of an isosceles triangle in which a Isosceles Triangle Inscribed In A Circle Suppose ab¯ ¯¯¯¯¯¯¯ is a diameter of a circle and c is a point on the circle different from a and b as in the picture below: Find the angles in the three minor segments of the circle cut off by the sides of this triangle. Express the inscribed circle’s radius in terms of the base ac and the height.. Isosceles Triangle Inscribed In A Circle.
From www.transtutors.com
(Get Answer) For the isosceles triangle inscribed in a circle of Isosceles Triangle Inscribed In A Circle Consider isosceles triangle abc (ав=вс). An isosceles triangle is inscribed in a circle. Draw height bk in it. If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: Show that triangles cob and coa are both isosceles triangles. A circle is inscribed in an isosceles with the. Isosceles Triangle Inscribed In A Circle.
From www.teachoo.com
Show that triangle of maximum area that can be inscribed in a circle Isosceles Triangle Inscribed In A Circle A circle is inscribed in an isosceles with the given dimensions. Draw height bk in it. An isosceles triangle is inscribed in a circle. Consider isosceles triangle abc (ав=вс). If ch c h is altitude (ch ⊥ ab, h ∈ ab) (c h ⊥ a b, h ∈ a b) and cj: A b c o 32° 74° 74° solution. Isosceles Triangle Inscribed In A Circle.