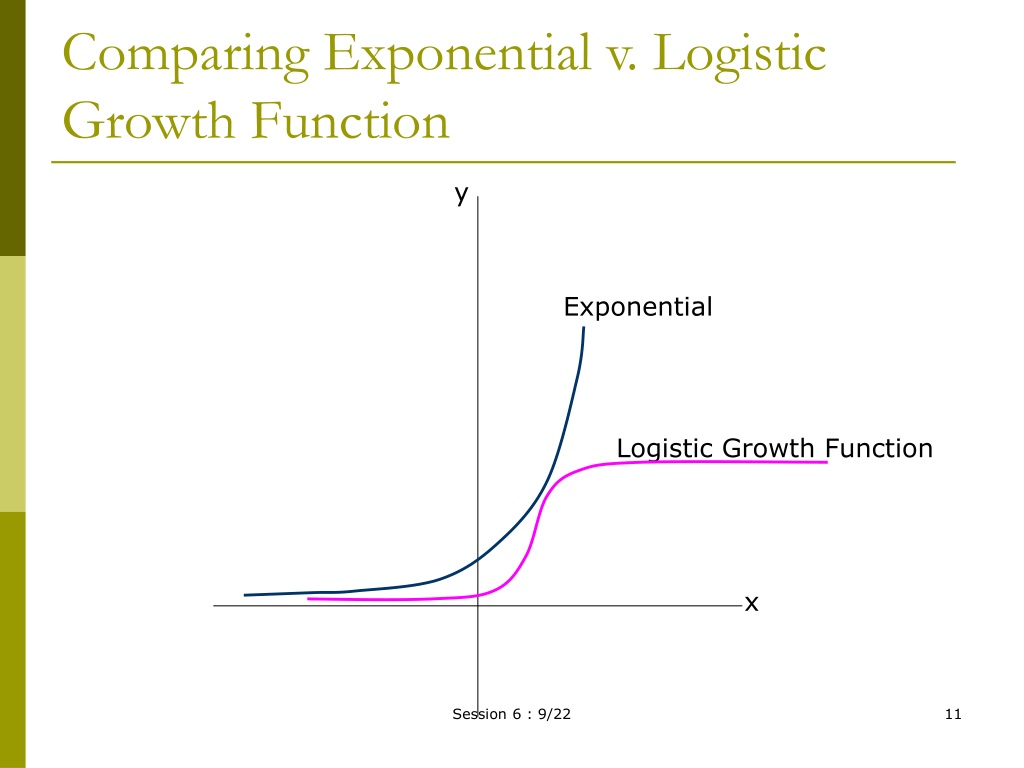
Logistic Vs Logarithmic Growth . The logistic growth model has a maximum population called the carrying capacity. Use the properties of logarithms to solve. In a confined environment the growth. What are the underlying principles of how populations change over time? What you’ll learn to do: The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). Evaluate and rewrite logarithms using the properties of logarithms. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant. Evaluate and rewrite logarithms using the properties of logarithms. Two basic principles are involved, the idea of exponential growth and its ultimate control. As the population grows, the number of individuals in the population grows to the carrying capacity. Use the properties of logarithms to solve problems involving logistic growth. Use the properties of logarithms to solve exponential models for time.
from www.slideserve.com
Two basic principles are involved, the idea of exponential growth and its ultimate control. Evaluate and rewrite logarithms using the properties of logarithms. Use the properties of logarithms to solve exponential models for time. The logistic growth model has a maximum population called the carrying capacity. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant. What you’ll learn to do: Use the properties of logarithms to solve problems involving logistic growth. Evaluate and rewrite logarithms using the properties of logarithms. What are the underlying principles of how populations change over time? In a confined environment the growth.
PPT Exponential and Logarithmic Functions PowerPoint Presentation
Logistic Vs Logarithmic Growth Two basic principles are involved, the idea of exponential growth and its ultimate control. Evaluate and rewrite logarithms using the properties of logarithms. Evaluate and rewrite logarithms using the properties of logarithms. Use the properties of logarithms to solve exponential models for time. What you’ll learn to do: In a confined environment the growth. What are the underlying principles of how populations change over time? The logistic growth model has a maximum population called the carrying capacity. The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). As the population grows, the number of individuals in the population grows to the carrying capacity. Use the properties of logarithms to solve. Two basic principles are involved, the idea of exponential growth and its ultimate control. Use the properties of logarithms to solve problems involving logistic growth. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant.
From www.geogebra.org
Logistic vs. Exponential Growth Models GeoGebra Logistic Vs Logarithmic Growth Use the properties of logarithms to solve. Use the properties of logarithms to solve problems involving logistic growth. Use the properties of logarithms to solve exponential models for time. The logistic growth model has a maximum population called the carrying capacity. Two basic principles are involved, the idea of exponential growth and its ultimate control. What you’ll learn to do:. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT 4.8 Exponential and Logarithmic Models PowerPoint Presentation Logistic Vs Logarithmic Growth As the population grows, the number of individuals in the population grows to the carrying capacity. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b. Logistic Vs Logarithmic Growth.
From differencebtw.com
Exponential Growth vs. Logistic Growth Know the Difference Logistic Vs Logarithmic Growth Evaluate and rewrite logarithms using the properties of logarithms. As the population grows, the number of individuals in the population grows to the carrying capacity. Use the properties of logarithms to solve exponential models for time. Use the properties of logarithms to solve. In a confined environment the growth. The logistic growth model has a maximum population called the carrying. Logistic Vs Logarithmic Growth.
From www.researchgate.net
14 Exponential (a) and logistic (b) curves describing population Logistic Vs Logarithmic Growth The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). What are the underlying principles of how populations change over time? In a confined environment the growth. Use the properties of logarithms to solve. Use the properties of logarithms to solve problems involving logistic growth. As the population grows,. Logistic Vs Logarithmic Growth.
From www.animalia-life.club
Logistic Growth Graph Logistic Vs Logarithmic Growth A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant. What you’ll learn to do: The logistic growth model has a maximum population. Logistic Vs Logarithmic Growth.
From jamesclear.com
The 2 Types of Growth Which Growth Curve Are You Following? Logistic Vs Logarithmic Growth A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant. Evaluate and rewrite logarithms using the properties of logarithms. The logistic growth model. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT The mechanisms of Disease Spread and Population Growth PowerPoint Logistic Vs Logarithmic Growth What are the underlying principles of how populations change over time? Evaluate and rewrite logarithms using the properties of logarithms. Two basic principles are involved, the idea of exponential growth and its ultimate control. The logistic growth model has a maximum population called the carrying capacity. As the population grows, the number of individuals in the population grows to the. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Exponential and Logarithmic Functions PowerPoint Presentation Logistic Vs Logarithmic Growth The logistic growth model has a maximum population called the carrying capacity. The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). What you’ll learn to do: Use the properties of logarithms to solve problems involving logistic growth. Use the properties of logarithms to solve exponential models for time.. Logistic Vs Logarithmic Growth.
From www.researchgate.net
Examples of the logistic growth curve A) logistic growth over time Logistic Vs Logarithmic Growth A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant. Use the properties of logarithms to solve. Two basic principles are involved, the. Logistic Vs Logarithmic Growth.
From ar.inspiredpencil.com
Logistic Growth Graph Logistic Vs Logarithmic Growth What are the underlying principles of how populations change over time? Two basic principles are involved, the idea of exponential growth and its ultimate control. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is. Logistic Vs Logarithmic Growth.
From zhuanlan.zhihu.com
Logit模型和Logistic模型有什么区别? 知乎 Logistic Vs Logarithmic Growth Use the properties of logarithms to solve exponential models for time. Evaluate and rewrite logarithms using the properties of logarithms. The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). Use the properties of logarithms to solve problems involving logistic growth. What you’ll learn to do: In a confined. Logistic Vs Logarithmic Growth.
From www.youtube.com
EXPONENTIAL & LOGISTIC GROWTH POPULATION GROWTH CURVES IN ECOLOGY Logistic Vs Logarithmic Growth What are the underlying principles of how populations change over time? The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). As the population grows, the number of individuals in the population grows to the carrying capacity. Evaluate and rewrite logarithms using the properties of logarithms. Evaluate and rewrite. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Thurs. 9/5/13 PowerPoint Presentation, free download ID1849175 Logistic Vs Logarithmic Growth Use the properties of logarithms to solve exponential models for time. In a confined environment the growth. As the population grows, the number of individuals in the population grows to the carrying capacity. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 +. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Chapter 5 PowerPoint Presentation ID466785 Logistic Vs Logarithmic Growth Use the properties of logarithms to solve exponential models for time. In a confined environment the growth. Use the properties of logarithms to solve. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the. Logistic Vs Logarithmic Growth.
From cmapspublic3.ihmc.us
Population Growth Ch. 11 Logistic Vs Logarithmic Growth The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). Evaluate and rewrite logarithms using the properties of logarithms. In a confined environment the growth. Use the properties of logarithms to solve. What are the underlying principles of how populations change over time? Two basic principles are involved, the. Logistic Vs Logarithmic Growth.
From www.youtube.com
Population Growth Models Exponential, Logistic... Explained! YouTube Logistic Vs Logarithmic Growth Use the properties of logarithms to solve. Evaluate and rewrite logarithms using the properties of logarithms. The logistic growth model has a maximum population called the carrying capacity. The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). A function of the form f (x) = c 1+ae−bx f. Logistic Vs Logarithmic Growth.
From www.askdifference.com
Exponential Growth vs. Logistic Growth — What’s the Difference? Logistic Vs Logarithmic Growth Evaluate and rewrite logarithms using the properties of logarithms. Use the properties of logarithms to solve exponential models for time. As the population grows, the number of individuals in the population grows to the carrying capacity. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a. Logistic Vs Logarithmic Growth.
From www.deanyeong.com
The Two Types of Growth Dean Yeong Logistic Vs Logarithmic Growth Use the properties of logarithms to solve problems involving logistic growth. The logistic growth model has a maximum population called the carrying capacity. As the population grows, the number of individuals in the population grows to the carrying capacity. Evaluate and rewrite logarithms using the properties of logarithms. Use the properties of logarithms to solve. A function of the form. Logistic Vs Logarithmic Growth.
From www.youtube.com
Logistic Growth Function and Differential Equations YouTube Logistic Vs Logarithmic Growth The logistic growth model has a maximum population called the carrying capacity. What are the underlying principles of how populations change over time? Use the properties of logarithms to solve problems involving logistic growth. Evaluate and rewrite logarithms using the properties of logarithms. Use the properties of logarithms to solve. In a confined environment the growth. The logistic growth model. Logistic Vs Logarithmic Growth.
From systry.com
Exponential and Logarithmic Models Systry Logistic Vs Logarithmic Growth Two basic principles are involved, the idea of exponential growth and its ultimate control. Evaluate and rewrite logarithms using the properties of logarithms. The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). As the population grows, the number of individuals in the population grows to the carrying capacity.. Logistic Vs Logarithmic Growth.
From www.sliderbase.com
The Logistic Model and Real Populations Logistic Vs Logarithmic Growth As the population grows, the number of individuals in the population grows to the carrying capacity. Use the properties of logarithms to solve. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying. Logistic Vs Logarithmic Growth.
From www.animalia-life.club
Logistic Growth Graph Logistic Vs Logarithmic Growth Use the properties of logarithms to solve problems involving logistic growth. In a confined environment the growth. Use the properties of logarithms to solve exponential models for time. As the population grows, the number of individuals in the population grows to the carrying capacity. The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying. Logistic Vs Logarithmic Growth.
From pediaa.com
Difference Between Exponential and Logistic Growth Definition Logistic Vs Logarithmic Growth Use the properties of logarithms to solve exponential models for time. The logistic growth model has a maximum population called the carrying capacity. As the population grows, the number of individuals in the population grows to the carrying capacity. What are the underlying principles of how populations change over time? The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the. Logistic Vs Logarithmic Growth.
From www.geeksforgeeks.org
Logistic Population Growth Definition, Factors, Graph, Examples, FAQs Logistic Vs Logarithmic Growth What are the underlying principles of how populations change over time? As the population grows, the number of individuals in the population grows to the carrying capacity. Use the properties of logarithms to solve problems involving logistic growth. Use the properties of logarithms to solve. Two basic principles are involved, the idea of exponential growth and its ultimate control. Use. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Chapter 8 Population Ecology PowerPoint Presentation, free Logistic Vs Logarithmic Growth What you’ll learn to do: A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant. In a confined environment the growth. The logistic. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Ecology PowerPoint Presentation, free download ID9221127 Logistic Vs Logarithmic Growth What are the underlying principles of how populations change over time? Evaluate and rewrite logarithms using the properties of logarithms. What you’ll learn to do: In a confined environment the growth. The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). Use the properties of logarithms to solve. A. Logistic Vs Logarithmic Growth.
From www.numerade.com
SOLVEDIdentify each model as exponential growth, exponential decay Logistic Vs Logarithmic Growth Evaluate and rewrite logarithms using the properties of logarithms. In a confined environment the growth. What are the underlying principles of how populations change over time? The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). Evaluate and rewrite logarithms using the properties of logarithms. What you’ll learn to. Logistic Vs Logarithmic Growth.
From ahurford.github.io
Chapter 2 Exponential vs Logistic Growth BIOL 2600 Principles of Ecology Logistic Vs Logarithmic Growth The logistic growth model is \[f(x)=\dfrac{c}{1+ae^{−bx}}\] where \(\dfrac{c}{1+a}\) is the initial value \(c\) is the carrying capacity, or limiting value \(b\). Evaluate and rewrite logarithms using the properties of logarithms. In a confined environment the growth. What you’ll learn to do: A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e −. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Chapter 3 Exponential, Logistic, and Logarithmic Functions Logistic Vs Logarithmic Growth Use the properties of logarithms to solve exponential models for time. The logistic growth model has a maximum population called the carrying capacity. Evaluate and rewrite logarithms using the properties of logarithms. Use the properties of logarithms to solve. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Population Dynamics, Carrying Capacity, and Conservation Biology Logistic Vs Logarithmic Growth What you’ll learn to do: Use the properties of logarithms to solve problems involving logistic growth. A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT AP Environmental Science Population Dynamics, Carrying Capacity Logistic Vs Logarithmic Growth The logistic growth model has a maximum population called the carrying capacity. Use the properties of logarithms to solve. Two basic principles are involved, the idea of exponential growth and its ultimate control. In a confined environment the growth. Use the properties of logarithms to solve exponential models for time. As the population grows, the number of individuals in the. Logistic Vs Logarithmic Growth.
From www.slideserve.com
PPT Population Ecology PowerPoint Presentation, free download ID Logistic Vs Logarithmic Growth Use the properties of logarithms to solve. Two basic principles are involved, the idea of exponential growth and its ultimate control. Evaluate and rewrite logarithms using the properties of logarithms. Evaluate and rewrite logarithms using the properties of logarithms. What you’ll learn to do: As the population grows, the number of individuals in the population grows to the carrying capacity.. Logistic Vs Logarithmic Growth.
From www.researchgate.net
Comparing the fit of logistic and exponential growth for Ebola 201415 Logistic Vs Logarithmic Growth A function of the form f (x) = c 1+ae−bx f (x) = c 1 + a e − b x where c 1+a c 1 + a is the initial value, c c is the carrying capacity, or limiting value, and b b is a constant. Use the properties of logarithms to solve problems involving logistic growth. What you’ll. Logistic Vs Logarithmic Growth.
From www.tjmahr.com
Anatomy of a logistic growth curve Higher Order Functions Logistic Vs Logarithmic Growth In a confined environment the growth. Use the properties of logarithms to solve problems involving logistic growth. What you’ll learn to do: Use the properties of logarithms to solve exponential models for time. As the population grows, the number of individuals in the population grows to the carrying capacity. Evaluate and rewrite logarithms using the properties of logarithms. What are. Logistic Vs Logarithmic Growth.
From faculty.uca.edu
Population Ecology Logistic Vs Logarithmic Growth Use the properties of logarithms to solve problems involving logistic growth. Two basic principles are involved, the idea of exponential growth and its ultimate control. Evaluate and rewrite logarithms using the properties of logarithms. What you’ll learn to do: Evaluate and rewrite logarithms using the properties of logarithms. In a confined environment the growth. The logistic growth model has a. Logistic Vs Logarithmic Growth.