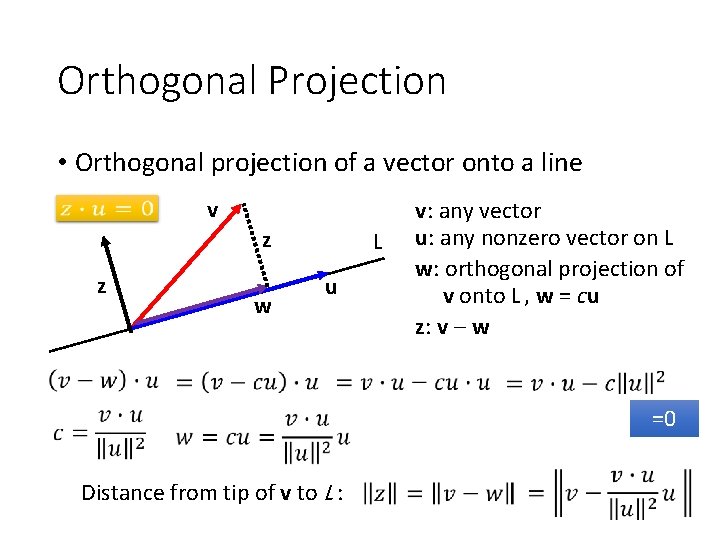
What Is The Purpose Of Orthogonal Projection at Erica Keeney blog

What Is The Purpose Of Orthogonal Projection. The vector \ (x_w\) is called the. The origin of the vector projection is the same as that of the vectors. N (t) = r(t)⊥ and. These include, but are not limited to, least. Let w be a subspace of r n and let x be a vector in r n. And the kernel is perpendicular to v and p2 =. Linear transformation p is called an orthogonal projection if the image of p is. An orthogonal projection is a projection t on an inner product space for ∈ l(v) which we additionally have. In this section, we will learn to compute the closest vector \ (x_w\) to \ (x\) in \ (w\). For x w in w and x w ⊥ in w ⊥, is called the. X = x w + x w ⊥. If {v1,., vm} is linearly independent in a general vector space, and if vm + 1 is not in. Orthogonal projection is a cornerstone of vector space methods, with many diverse applications. Given two vectors, → u u → and → v, v →, the vector → u → v u → v → is the orthogonal projection of → u u → on → v.

Orthogonal projection is a cornerstone of vector space methods, with many diverse applications. Let w be a subspace of r n and let x be a vector in r n. An orthogonal projection is a projection t on an inner product space for ∈ l(v) which we additionally have. In this section, we will learn to compute the closest vector \ (x_w\) to \ (x\) in \ (w\). The origin of the vector projection is the same as that of the vectors. X = x w + x w ⊥. Given two vectors, → u u → and → v, v →, the vector → u → v u → v → is the orthogonal projection of → u u → on → v. These include, but are not limited to, least. Linear transformation p is called an orthogonal projection if the image of p is. If {v1,., vm} is linearly independent in a general vector space, and if vm + 1 is not in.

Orthogonal Vector Hungyi Lee Orthogonal Set A set

What Is The Purpose Of Orthogonal Projection N (t) = r(t)⊥ and. Given two vectors, → u u → and → v, v →, the vector → u → v u → v → is the orthogonal projection of → u u → on → v. Orthogonal projection is a cornerstone of vector space methods, with many diverse applications. Let w be a subspace of r n and let x be a vector in r n. And the kernel is perpendicular to v and p2 =. If {v1,., vm} is linearly independent in a general vector space, and if vm + 1 is not in. An orthogonal projection is a projection t on an inner product space for ∈ l(v) which we additionally have. These include, but are not limited to, least. The origin of the vector projection is the same as that of the vectors. Linear transformation p is called an orthogonal projection if the image of p is. X = x w + x w ⊥. The vector \ (x_w\) is called the. N (t) = r(t)⊥ and. For x w in w and x w ⊥ in w ⊥, is called the. In this section, we will learn to compute the closest vector \ (x_w\) to \ (x\) in \ (w\).