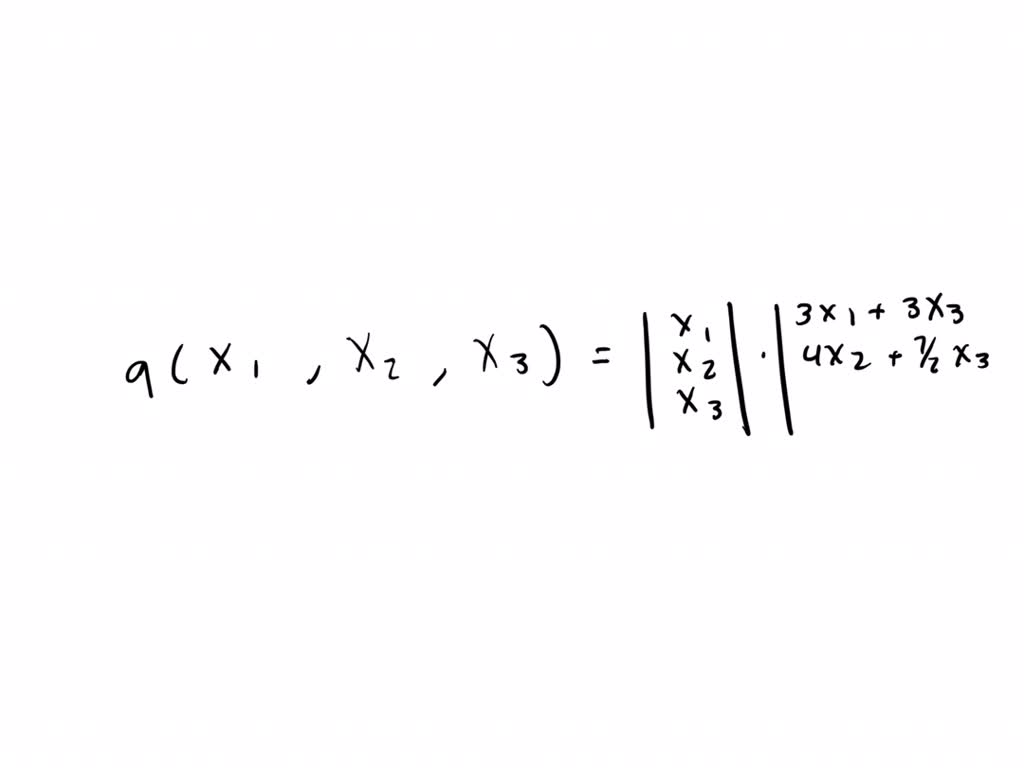Orthogonal Matrix That Diagonalizes . An [latex]n\times n[/latex] matrix [latex]a[/latex] is said to be orthogonally diagonalizable if there are an. an \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a. I found the third eigenvector by simply taking the. in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal. — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by. then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns are the vectors in \(b\) (see theorem 9.2.4). — b) find an orthogonal matrix that diagonalises the matrix a. — diagonal matrix: A symmetric matrix) is a diagonalization by. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. real symmetric matrices are diagonalizable by orthogonal matrices; — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. Find an orthogonal matrix $p$ and a. You find the eigenvalues, you find.
from www.numerade.com
We call a square array of numbers a diagonal matrix if it is of the. thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: An [latex]n\times n[/latex] matrix [latex]a[/latex] is said to be orthogonally diagonalizable if there are an. in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal. — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. — diagonal matrix: — in this video, we orthogonally diagonalize a symmetric matrix. I.e., given a real symmetric matrix , is diagonal for some. — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by.
SOLVEDFor each of the following quadratic forms, determine an
Orthogonal Matrix That Diagonalizes — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of \ (3\) and. I found the third eigenvector by simply taking the. — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of \ (3\) and. — in this video, we orthogonally diagonalize a symmetric matrix. an \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a. then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns are the vectors in \(b\) (see theorem 9.2.4). — b) find an orthogonal matrix that diagonalises the matrix a. Not only can we factor e œ t ht , but we can find an. Find an orthogonal matrix $p$ and a. — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. A= 0 @ 1 0 2 0 1 2 2 2 0 1 a: the symmetric matrix $a$ below has distinct eigenvalues $−6, −12$ and $−18$. A symmetric matrix) is a diagonalization by. — i want to prove that all orthogonal matrices are diagonalizable over $c$. I.e., given a real symmetric matrix , is diagonal for some. in linear algebra, an orthogonal diagonalization of a normal matrix (e.g.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal Orthogonal Matrix That Diagonalizes the symmetric matrix $a$ below has distinct eigenvalues $−6, −12$ and $−18$. then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns are the vectors in \(b\) (see theorem 9.2.4). A symmetric matrix) is a diagonalization by. — i want to prove that all orthogonal matrices are diagonalizable over $c$. — in. Orthogonal Matrix That Diagonalizes.
From www.gauthmath.com
Solved Find the orthogonal matrix P that diagonalizes A Where A Orthogonal Matrix That Diagonalizes the symmetric matrix $a$ below has distinct eigenvalues $−6, −12$ and $−18$. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. An [latex]n\times n[/latex] matrix [latex]a[/latex] is said to be orthogonally diagonalizable if there are an. A= 0 @ 1 0 2 0 1 2 2 2. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Find an orthogonal matrix Q that diagonalizes this Orthogonal Matrix That Diagonalizes — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal. Find an orthogonal matrix $p$ and a. I found the third eigenvector by simply taking the. the symmetric matrix $a$ below has. Orthogonal Matrix That Diagonalizes.
From www.youtube.com
Week 10 Symmetric matrices and orthogonal diagonalization YouTube Orthogonal Matrix That Diagonalizes then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns are the vectors in \(b\) (see theorem 9.2.4). — in this video, we orthogonally diagonalize a symmetric matrix. Not only can we factor e œ t ht , but we can find an. — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix. Orthogonal Matrix That Diagonalizes.
From www.numerade.com
SOLVEDFor each of the following quadratic forms, determine an Orthogonal Matrix That Diagonalizes A= 0 @ 1 0 2 0 1 2 2 2 0 1 a: You find the eigenvalues, you find. I found the third eigenvector by simply taking the. We call a square array of numbers a diagonal matrix if it is of the. real symmetric matrices are diagonalizable by orthogonal matrices; I know that a matrix is orthogonal. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Orthogonal Matrix That Diagonalizes — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. I.e., given a real symmetric matrix , is diagonal for some. A symmetric matrix) is a diagonalization by. I found the third eigenvector by simply taking the. You find the eigenvalues, you find. An [latex]n\times n[/latex] matrix [latex]a[/latex] is said to be orthogonally diagonalizable. Orthogonal Matrix That Diagonalizes.
From medium.com
[Linear Algebra] 9. Properties of orthogonal matrices by jun94 jun Orthogonal Matrix That Diagonalizes then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns are the vectors in \(b\) (see theorem 9.2.4). A= 0 @ 1 0 2 0 1 2 2 2 0 1 a: Find an orthogonal matrix $p$ and a. A symmetric matrix) is a diagonalization by. — in this video, we orthogonally diagonalize a. Orthogonal Matrix That Diagonalizes.
From www.youtube.com
Linear Algebra Example Problems Diagonalizing a Matrix YouTube Orthogonal Matrix That Diagonalizes then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns are the vectors in \(b\) (see theorem 9.2.4). — b) find an orthogonal matrix that diagonalises the matrix a. — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by. in linear algebra,. Orthogonal Matrix That Diagonalizes.
From kunduz.com
[ANSWERED] Find an orthogonal matrix Q that diagonalizes S e 4 Gl 1 31 Orthogonal Matrix That Diagonalizes Not only can we factor e œ t ht , but we can find an. I know that a matrix is orthogonal if. — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of \ (3\) and. then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns. Orthogonal Matrix That Diagonalizes.
From slideplayer.com
Chapter 6 Eigenvalues. ppt video online download Orthogonal Matrix That Diagonalizes I found the third eigenvector by simply taking the. an \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a. Not only can we factor e œ t ht , but we can find an. thus, an orthogonally diagonalizable matrix is a special kind of diagonalizable matrix: An. Orthogonal Matrix That Diagonalizes.
From www.gauthmath.com
Solved Find the orthogonal matrix P that diagonalizes A Where A Orthogonal Matrix That Diagonalizes in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal. $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of \ (3\) and. real symmetric matrices are diagonalizable. Orthogonal Matrix That Diagonalizes.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Orthogonal Matrix That Diagonalizes $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. A symmetric matrix) is a diagonalization by. A= 0 @ 1 0 2 0 1 2 2 2 0 1. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved 1. (30 pts) Let 14 2 007 2 4 0 0 A = 0 0 4 2 LO 0 2 4 Orthogonal Matrix That Diagonalizes in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by. — in this video, we orthogonally diagonalize a symmetric matrix. — orthogonally diagonalizable matrices. Orthogonal Matrix That Diagonalizes.
From www.numerade.com
SOLVEDFor the following matrices find an orthogonal matrix 𝐐 which Orthogonal Matrix That Diagonalizes A= 0 @ 1 0 2 0 1 2 2 2 0 1 a: find an orthogonal matrix qthat diagonalizes the symmetric matrix: A symmetric matrix) is a diagonalization by. — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by. — orthogonally diagonalizable matrices 024297 an \(n. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Orthogonally diagonalize the matrix below, giving an Orthogonal Matrix That Diagonalizes — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. — diagonal matrix: A symmetric matrix) is a diagonalization by. — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. — in this. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Orthogonally diagonalize matrix A given below; that Orthogonal Matrix That Diagonalizes — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. the symmetric matrix $a$ below has distinct eigenvalues $−6, −12$ and $−18$. I.e., given a real symmetric matrix , is diagonal for some. — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved 6. Find an orthogonal matrix Q that diagonalizes the Orthogonal Matrix That Diagonalizes then \(p^t a p\) is diagonal where \(p\) is the orthogonal matrix whose columns are the vectors in \(b\) (see theorem 9.2.4). You find the eigenvalues, you find. — b) find an orthogonal matrix that diagonalises the matrix a. — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. in. Orthogonal Matrix That Diagonalizes.
From semath.info
How to diagonalize a 3x3 matrix Example SEMATH INFO Orthogonal Matrix That Diagonalizes find an orthogonal matrix qthat diagonalizes the symmetric matrix: You find the eigenvalues, you find. $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: I.e., given a real symmetric matrix , is diagonal for some. I found the third eigenvector by simply taking the. the symmetric matrix $a$ below has distinct eigenvalues $−6, −12$ and $−18$.. Orthogonal Matrix That Diagonalizes.
From www.solutionspile.com
[Solved] 3b.[10p.] Find an orthogonal matrix Q that diagon Orthogonal Matrix That Diagonalizes You find the eigenvalues, you find. — b) find an orthogonal matrix that diagonalises the matrix a. An [latex]n\times n[/latex] matrix [latex]a[/latex] is said to be orthogonally diagonalizable if there are an. find an orthogonal matrix qthat diagonalizes the symmetric matrix: — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. . Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Produce a matrix P that diagonalizes the given matrix Orthogonal Matrix That Diagonalizes — in this video, we orthogonally diagonalize a symmetric matrix. — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. real symmetric matrices are diagonalizable by orthogonal matrices; $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: — i want to prove that all orthogonal matrices are diagonalizable. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved 9. Find an orthogonal matrix P such that P Orthogonal Matrix That Diagonalizes $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: I.e., given a real symmetric matrix , is diagonal for some. We call a square array of numbers a diagonal matrix if it is of the. You find the eigenvalues, you find. A symmetric matrix) is a diagonalization by. I know that a matrix is orthogonal if. then. Orthogonal Matrix That Diagonalizes.
From www.youtube.com
Orthogonally Diagonalize a Matrix YouTube Orthogonal Matrix That Diagonalizes — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. A= 0 @ 1 0 2 0 1 2 2 2 0 1 a: I found the third eigenvector by simply taking the. in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal.. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Find a matrix P^1 AP that diagonalizes A=[004 Orthogonal Matrix That Diagonalizes — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by. $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: — b) find an orthogonal matrix that diagonalises the matrix a. — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent.. Orthogonal Matrix That Diagonalizes.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Orthogonal Matrix That Diagonalizes I.e., given a real symmetric matrix , is diagonal for some. Find an orthogonal matrix $p$ and a. — in this video, we orthogonally diagonalize a symmetric matrix. An [latex]n\times n[/latex] matrix [latex]a[/latex] is said to be orthogonally diagonalizable if there are an. I know that a matrix is orthogonal if. We call a square array of numbers a. Orthogonal Matrix That Diagonalizes.
From www.numerade.com
SOLVEDFind the C matrix which diagonalizes the matrix M of Problem 1 Orthogonal Matrix That Diagonalizes an \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a. find an orthogonal matrix qthat diagonalizes the symmetric matrix: — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there is an invertible matrix \(p\) given by. the symmetric matrix $a$ below has. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved 57 1 Let A = . Find an orthogonal matrix P that Orthogonal Matrix That Diagonalizes Find an orthogonal matrix $p$ and a. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of \. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Let Orthogonal Matrix That Diagonalizes $\begingroup$ the same way you orthogonally diagonalize any symmetric matrix: A symmetric matrix) is a diagonalization by. real symmetric matrices are diagonalizable by orthogonal matrices; We call a square array of numbers a diagonal matrix if it is of the. — diagonal matrix: — an \(n\times n\) matrix \(a\) is diagonalizable if and only if there. Orthogonal Matrix That Diagonalizes.
From rebeccamorford.blogspot.com
Symmetric Matrix Orthogonally Diagonalizable Rebecca Morford's Orthogonal Matrix That Diagonalizes Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. — b) find an orthogonal matrix that diagonalises the matrix a. in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Find an orthogonal matrix Q that diagonalizes Orthogonal Matrix That Diagonalizes A symmetric matrix) is a diagonalization by. You find the eigenvalues, you find. Recall (theorem 5.5.3) that an n n matrix a is diagonalizable if and only if it has n linearly independent eigenvectors. in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal. thus, an orthogonally diagonalizable. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Find an orthogonal matrix Q that diagonalizes the Orthogonal Matrix That Diagonalizes — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. A= 0 @ 1 0 2 0 1 2 2 2 0 1 a: the symmetric matrix $a$ below has distinct eigenvalues $−6, −12$ and $−18$. in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose. Orthogonal Matrix That Diagonalizes.
From www.bartleby.com
Answered Orthogonally diagonalize the matrix,… bartleby Orthogonal Matrix That Diagonalizes — in this video, we orthogonally diagonalize a symmetric matrix. We call a square array of numbers a diagonal matrix if it is of the. — b) find an orthogonal matrix that diagonalises the matrix a. — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. real symmetric matrices are diagonalizable. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Find an orthogonal matrix Q that diagonalizes this Orthogonal Matrix That Diagonalizes I know that a matrix is orthogonal if. You find the eigenvalues, you find. an \(n \times n\) matrix \(a\) is orthogonally diagonalizable if there is an orthogonal matrix \(p\) such that \(p^{\tr}ap\) is a. in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. Not only can we factor e œ t ht , but we. Orthogonal Matrix That Diagonalizes.
From www.chegg.com
Solved Find an orthogonal matrix Q that diagonalizes this Orthogonal Matrix That Diagonalizes — the matrix $a$ is symmetric so orthogonally diagonalizable, so the eigenvectors they are independent. — i want to prove that all orthogonal matrices are diagonalizable over $c$. — orthogonally diagonalizable matrices 024297 an \(n \times n\) matrix \(a\) is said to be orthogonally. An [latex]n\times n[/latex] matrix [latex]a[/latex] is said to be orthogonally diagonalizable if there. Orthogonal Matrix That Diagonalizes.
From www.youtube.com
Diagonalisation of matrix, example I YouTube Orthogonal Matrix That Diagonalizes in linear algebra, an orthogonal diagonalization of a normal matrix (e.g. in linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal. — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of \ (3\) and. — diagonal matrix: I. Orthogonal Matrix That Diagonalizes.
From rebeccamorford.blogspot.com
Symmetric Matrix Orthogonally Diagonalizable Rebecca Morford's Orthogonal Matrix That Diagonalizes — i want to prove that all orthogonal matrices are diagonalizable over $c$. — the diagonal matrix \ (d\) has the geometric effect of stretching vectors horizontally by a factor of \ (3\) and. — diagonal matrix: We call a square array of numbers a diagonal matrix if it is of the. A symmetric matrix) is a. Orthogonal Matrix That Diagonalizes.