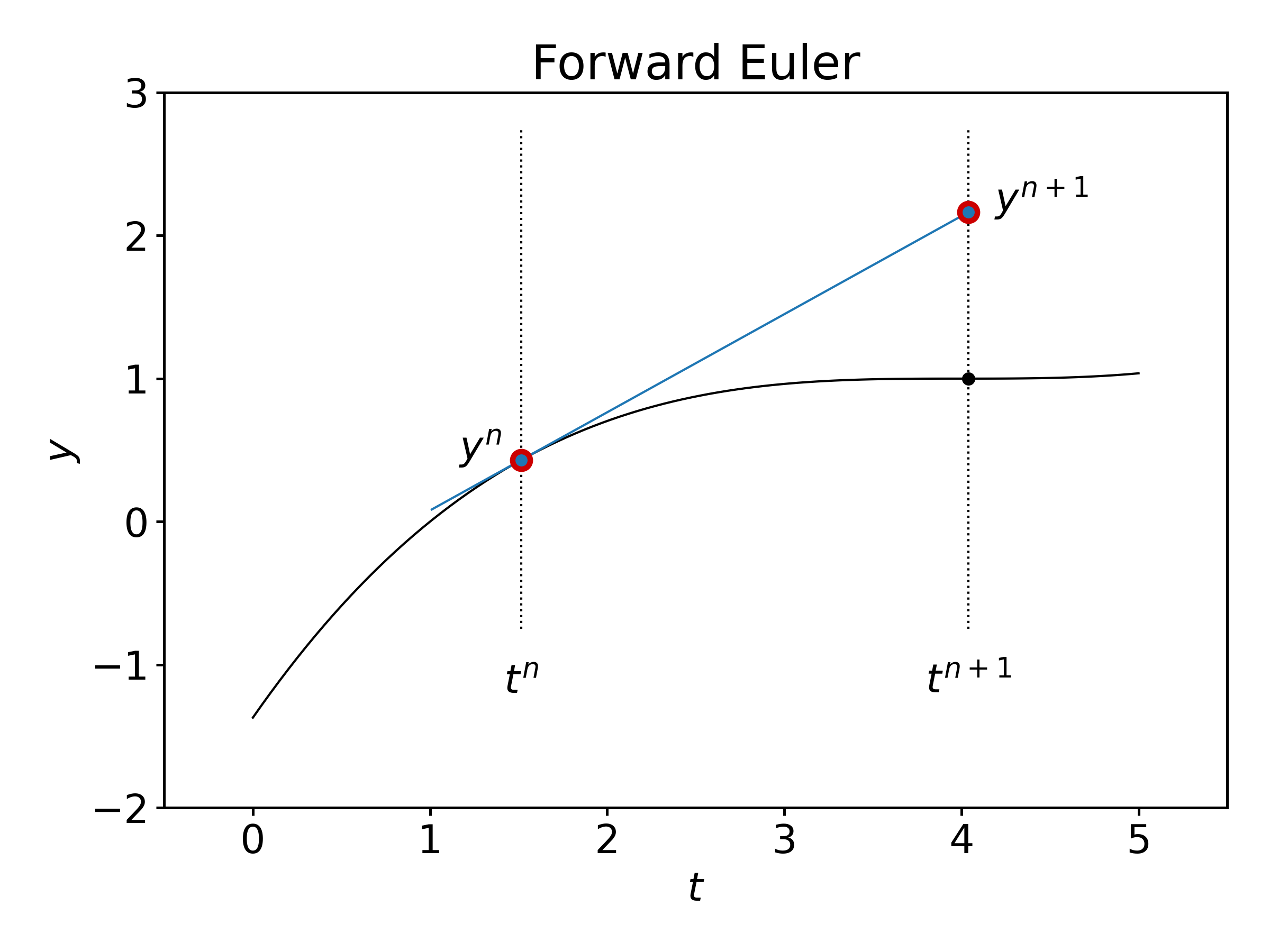
Runge Kutta 4 Stability . In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. We now define the stability of. Different ode solvers have different stability properties and are stable over larger values of \(h\). In general, only implicit methods are candidates for stiff. For example the implicit euler method is. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1).
from aquaulb.github.io
Different ode solvers have different stability properties and are stable over larger values of \(h\). The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. We now define the stability of. In general, only implicit methods are candidates for stiff. For example the implicit euler method is.
4. RungeKutta methods — Solving Partial Differential Equations MOOC
Runge Kutta 4 Stability The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). We now define the stability of. Different ode solvers have different stability properties and are stable over larger values of \(h\). In general, only implicit methods are candidates for stiff. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. For example the implicit euler method is.
From www.youtube.com
4th order RungeKutta method with Matlab Demo YouTube Runge Kutta 4 Stability We now define the stability of. In general, only implicit methods are candidates for stiff. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). For example the implicit euler method is. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of. Runge Kutta 4 Stability.
From joimfnrdb.blob.core.windows.net
Runge Kutta Definition at Alexander Ehmann blog Runge Kutta 4 Stability In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. We now define the stability of. In general, only implicit methods are candidates for stiff. Different ode solvers have different stability properties and are stable over larger values of \(h\). For. Runge Kutta 4 Stability.
From www.researchgate.net
Stability region arrows denote stability inside the corresponding curve Runge Kutta 4 Stability In general, only implicit methods are candidates for stiff. Different ode solvers have different stability properties and are stable over larger values of \(h\). The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded. Runge Kutta 4 Stability.
From www.youtube.com
Péndulo SImple Solución po Runge Kutta 4 YouTube Runge Kutta 4 Stability The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. Different ode solvers have different stability properties and are stable over larger values of \(h\). We now. Runge Kutta 4 Stability.
From www.researchgate.net
Optimal stability regions for a sstages second order RungeKutta Runge Kutta 4 Stability For example the implicit euler method is. We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. In general, only implicit methods are candidates for stiff. Different ode solvers have different stability properties and are. Runge Kutta 4 Stability.
From dokumen.tips
(PDF) Stability regions of RungeKutta methods TU/e · Stability Runge Kutta 4 Stability We now define the stability of. Different ode solvers have different stability properties and are stable over larger values of \(h\). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. The backward (or implicit) euler method y n+1 = y. Runge Kutta 4 Stability.
From www.physagreg.fr
Physagreg méthodes numériques pour la physique, Euler et RungeKutta Runge Kutta 4 Stability For example the implicit euler method is. Different ode solvers have different stability properties and are stable over larger values of \(h\). The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded by 1. Runge Kutta 4 Stability.
From deepai.org
FractionalStep RungeKutta Methods Representation and Linear Runge Kutta 4 Stability We now define the stability of. Different ode solvers have different stability properties and are stable over larger values of \(h\). In general, only implicit methods are candidates for stiff. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). For example the implicit euler method is. In order to plot the stability region, we can. Runge Kutta 4 Stability.
From www.youtube.com
EDO Método de RungeKutta de Ordem 4 YouTube Runge Kutta 4 Stability The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). For example the implicit euler method is. In general, only implicit methods are candidates for stiff. We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of. Runge Kutta 4 Stability.
From waldermarkur.blogspot.com
Runge Kutta 4Th Order MATLAB Numerical Methods How to use the Runge Runge Kutta 4 Stability The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). For example the implicit euler method is. In general, only implicit methods are candidates for stiff. We now define the stability of. Different ode solvers have different stability properties and are stable over larger values of \(h\). In order to plot the stability region, we can. Runge Kutta 4 Stability.
From www.haroldserrano.com
Visualizing the RungeKutta Method — Harold Serrano Game Engine Developer Runge Kutta 4 Stability Different ode solvers have different stability properties and are stable over larger values of \(h\). We now define the stability of. In general, only implicit methods are candidates for stiff. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. For. Runge Kutta 4 Stability.
From joimfnrdb.blob.core.windows.net
Runge Kutta Definition at Alexander Ehmann blog Runge Kutta 4 Stability We now define the stability of. Different ode solvers have different stability properties and are stable over larger values of \(h\). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. The backward (or implicit) euler method y n+1 = y. Runge Kutta 4 Stability.
From www.researchgate.net
2 The absolute stability region of the fourthorder RungeKutta method Runge Kutta 4 Stability For example the implicit euler method is. In general, only implicit methods are candidates for stiff. We now define the stability of. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of. Runge Kutta 4 Stability.
From www.youtube.com
MATLAB Numerical Methods How to use the Runge Kutta 4th order method Runge Kutta 4 Stability We now define the stability of. For example the implicit euler method is. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. In general, only implicit methods are candidates for stiff. Different ode solvers have different stability properties and are. Runge Kutta 4 Stability.
From www.slideserve.com
PPT Runge 4 th Order Method PowerPoint Presentation, free download Runge Kutta 4 Stability For example the implicit euler method is. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). We now define the stability of. Different ode solvers have different stability properties and are stable over larger values of \(h\). In order to plot the stability region, we can set the stability function to be bounded by 1. Runge Kutta 4 Stability.
From www.researchgate.net
THE ABSOLUTE STABILITY REGION OF THE FOURTHORDER RUNGEKUTTA METHOD Runge Kutta 4 Stability For example the implicit euler method is. Different ode solvers have different stability properties and are stable over larger values of \(h\). In general, only implicit methods are candidates for stiff. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). We now define the stability of. In order to plot the stability region, we can. Runge Kutta 4 Stability.
From www.researchgate.net
The classical 4stage fourth order RungeKutta method for (11 Runge Kutta 4 Stability In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. We now define the stability of. In general, only implicit methods are candidates for stiff. For example the implicit euler method is. The backward (or implicit) euler method y n+1 =. Runge Kutta 4 Stability.
From www.researchgate.net
Stability region of the new RungeKutta method of Table 2. Download Runge Kutta 4 Stability We now define the stability of. In general, only implicit methods are candidates for stiff. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. For example the implicit euler method is. Different ode solvers have different stability properties and are. Runge Kutta 4 Stability.
From www.researchgate.net
Von Neumann stability domains for first five RungeKutta schemes. Left Runge Kutta 4 Stability The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. We now define the stability of. In general, only implicit methods are candidates for stiff. For example. Runge Kutta 4 Stability.
From www.scribd.com
RungeKutta 4thOrder Method and Hints PDF Integral Numerical Runge Kutta 4 Stability In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. Different ode solvers have different stability properties and are stable over larger values of \(h\). We now define the stability of. For example the implicit euler method is. In general, only. Runge Kutta 4 Stability.
From www.researchgate.net
(PDF) Stability Analysis of RungeKutta Methods for Runge Kutta 4 Stability The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In general, only implicit methods are candidates for stiff. Different ode solvers have different stability properties and are stable over larger values of \(h\). We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded. Runge Kutta 4 Stability.
From aquaulb.github.io
4. RungeKutta methods — Solving Partial Differential Equations MOOC Runge Kutta 4 Stability In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. In general, only implicit methods are candidates for stiff. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). Different ode solvers have different stability properties and. Runge Kutta 4 Stability.
From www.researchgate.net
Region of stability of the secondorder RungeKutta (RK2) method Runge Kutta 4 Stability Different ode solvers have different stability properties and are stable over larger values of \(h\). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). We now. Runge Kutta 4 Stability.
From www.chegg.com
Solved Consider the 4thorder RungeKutta method Find the Runge Kutta 4 Stability In general, only implicit methods are candidates for stiff. Different ode solvers have different stability properties and are stable over larger values of \(h\). The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the. Runge Kutta 4 Stability.
From gantovnik.com
192 4th order RungeKutta method Tips and Hints for Aerospace Engineers Runge Kutta 4 Stability In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. In general, only implicit methods are candidates for stiff. We now define the stability of. For example the implicit euler method is. Different ode solvers have different stability properties and are. Runge Kutta 4 Stability.
From www.youtube.com
Método de Runge Kutta de Cuarto Orden YouTube Runge Kutta 4 Stability Different ode solvers have different stability properties and are stable over larger values of \(h\). We now define the stability of. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). For example the implicit euler method is. In order to plot the stability region, we can set the stability function to be bounded by 1. Runge Kutta 4 Stability.
From www.youtube.com
Stability function of a RungeKutta method YouTube Runge Kutta 4 Stability We now define the stability of. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In general, only implicit methods are candidates for stiff. Different ode solvers have different stability properties and are stable over larger values of \(h\). For example the implicit euler method is. In order to plot the stability region, we can. Runge Kutta 4 Stability.
From www.researchgate.net
The regions of absolute stability for various ERK schemes. Download Runge Kutta 4 Stability Different ode solvers have different stability properties and are stable over larger values of \(h\). The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z,. Runge Kutta 4 Stability.
From dokumen.tips
(PDF) Stability of RungeKutta Methods DOKUMEN.TIPS Runge Kutta 4 Stability In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. Different ode solvers have different stability properties and are stable over larger values of \(h\). For example the implicit euler method is. In general, only implicit methods are candidates for stiff.. Runge Kutta 4 Stability.
From www.researchgate.net
Stability region of the fourth order RungeKutta method Download Runge Kutta 4 Stability In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. Different ode solvers have different stability properties and are stable over larger values of \(h\). For example the implicit euler method is. We now define the stability of. In general, only. Runge Kutta 4 Stability.
From www.youtube.com
A Matlab Code For Stability Region Runge Kutta 4 (Codigo de matlab de Runge Kutta 4 Stability We now define the stability of. In general, only implicit methods are candidates for stiff. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). For example the implicit euler method is. Different ode solvers have different stability properties and are stable over larger values of \(h\). In order to plot the stability region, we can. Runge Kutta 4 Stability.
From medium.com
Euler’s Method and Runge Kutta 4th Order Method in Python by Pushkar Runge Kutta 4 Stability We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). For example the implicit euler method is. Different ode solvers have. Runge Kutta 4 Stability.
From www.youtube.com
4thOrder Runge Kutta Method for ODEs YouTube Runge Kutta 4 Stability For example the implicit euler method is. We now define the stability of. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). Different ode solvers have. Runge Kutta 4 Stability.
From www.researchgate.net
Regions of absolute stability for the RungeKutta integration schemes Runge Kutta 4 Stability The backward (or implicit) euler method y n+1 = y n +hf(t n+1,y n+1). In general, only implicit methods are candidates for stiff. We now define the stability of. For example the implicit euler method is. In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of. Runge Kutta 4 Stability.
From www.youtube.com
Stability of RUNGE KUTTA METHOD ORDER.4 YouTube Runge Kutta 4 Stability Different ode solvers have different stability properties and are stable over larger values of \(h\). In order to plot the stability region, we can set the stability function to be bounded by 1 and solve for the values of z, then draw z in. In general, only implicit methods are candidates for stiff. The backward (or implicit) euler method y. Runge Kutta 4 Stability.