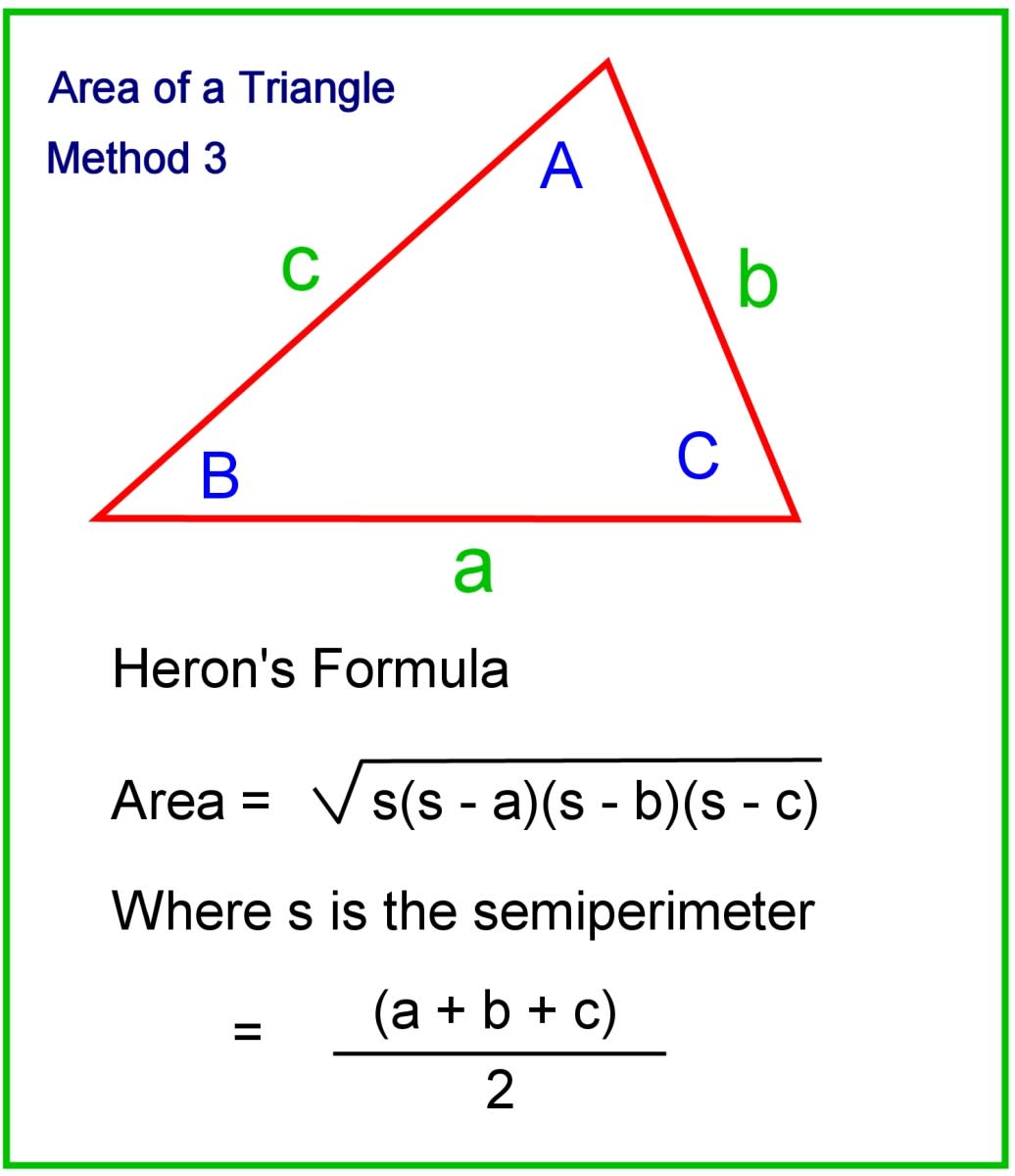
Cos Triangle Area . Areaδ = ½ ab sin c. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. The area of any triangle can be calculated using the formula: Perhaps the most familiar formula for the area. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. We will now develop a few different ways to calculate the area of a triangle. Watch this video to learn how to calculate the area of a triangle. To be able to calculate the. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any.
from owlcation.com
For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. Perhaps the most familiar formula for the area. We will now develop a few different ways to calculate the area of a triangle. To be able to calculate the. Areaδ = ½ ab sin c. Watch this video to learn how to calculate the area of a triangle. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle.
How to Calculate the Sides and Angles of Triangles Using Pythagoras
Cos Triangle Area \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. To be able to calculate the. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. We will now develop a few different ways to calculate the area of a triangle. Watch this video to learn how to calculate the area of a triangle. Perhaps the most familiar formula for the area. Areaδ = ½ ab sin c. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. The area of any triangle can be calculated using the formula:
From donsteward.blogspot.com
MEDIAN Don Steward mathematics teaching cosine rule Cos Triangle Area We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. Areaδ = ½. Cos Triangle Area.
From www.tes.com
The Cosine Rule Teaching Resources Cos Triangle Area Areaδ = ½ ab sin c. Perhaps the most familiar formula for the area. The area of any triangle can be calculated using the formula: We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. \ (\text {area of a triangle} = \frac {1}. Cos Triangle Area.
From thirdspacelearning.com
Area of a Triangle Trig GCSE Maths Steps, Examples & Worksheet Cos Triangle Area Perhaps the most familiar formula for the area. Areaδ = ½ ab sin c. We will now develop a few different ways to calculate the area of a triangle. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. \ (\text {area of a triangle} = \frac {1} {2}. Cos Triangle Area.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Cos Triangle Area \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 /. Cos Triangle Area.
From fullwallpaper.neocities.org
Area Of Triangle Sine Rule Cos Triangle Area Watch this video to learn how to calculate the area of a triangle. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. We will now develop a few different ways to calculate the area of a triangle. Perhaps the most familiar formula for. Cos Triangle Area.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Cos Triangle Area For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. Watch this video to learn how to calculate the area of a triangle. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding. Cos Triangle Area.
From cimt.org.uk
Section 4 Sine And Cosine Rule Cos Triangle Area We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. Perhaps the most familiar formula for the area. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Areaδ = ½ ab sin. Cos Triangle Area.
From www.studypool.com
SOLUTION Sine rule cosine rule area of triangle Studypool Cos Triangle Area Perhaps the most familiar formula for the area. Areaδ = ½ ab sin c. We will now develop a few different ways to calculate the area of a triangle. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. Watch this video to learn how to calculate the area of. Cos Triangle Area.
From danstestprep.com
How To Solve Hard SAT Math Problems Right Triangle Trigonometry (Part Cos Triangle Area Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. Watch this video to learn how to calculate the area of a triangle. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. We use the law of sines and law. Cos Triangle Area.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Owlcation Cos Triangle Area We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. Areaδ = ½ ab sin c. Watch this video to learn how to calculate the area of a triangle. The area of a triangle can be expressed using the lengths of two sides and. Cos Triangle Area.
From www.researchgate.net
Parameterization of the projections of a scalene triangle ABC from a Cos Triangle Area For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. The area of any triangle can be calculated using the formula: Perhaps the most familiar formula for the area. Cosines, and area of triangles formulas, notes, examples, and practice. Cos Triangle Area.
From www.youtube.com
OCR FSMQ Additional Mathematics (Old Spec) Lesson 21 Sine/Cosine Cos Triangle Area We will now develop a few different ways to calculate the area of a triangle. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Perhaps the most familiar formula. Cos Triangle Area.
From www.nagwa.com
Question Video Applying the Cosine Rule to Solve Triangles Nagwa Cos Triangle Area Watch this video to learn how to calculate the area of a triangle. To be able to calculate the. Areaδ = ½ ab sin c. Perhaps the most familiar formula for the area. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. The area of a triangle can be. Cos Triangle Area.
From hwtwom.blogspot.com
How To Find The Area Of A Triangle Cosine Rule howto Cos Triangle Area Areaδ = ½ ab sin c. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Perhaps the most familiar formula for the area. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. We use the law of. Cos Triangle Area.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Cos Triangle Area Areaδ = ½ ab sin c. We will now develop a few different ways to calculate the area of a triangle. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3. Cos Triangle Area.
From learningmagicsongbirds.z13.web.core.windows.net
Law Of Cosine Worksheets Cos Triangle Area To be able to calculate the. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. The area of any triangle can be calculated using the formula: Areaδ = ½ ab sin c. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides). Cos Triangle Area.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Cos Triangle Area Perhaps the most familiar formula for the area. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle.. Cos Triangle Area.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Cos Triangle Area Areaδ = ½ ab sin c. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. We will now develop a few different ways to calculate the area of a triangle. Watch this video to learn how to calculate. Cos Triangle Area.
From joigboxlt.blob.core.windows.net
Triangle Formula Cosine at Jenna Rockwell blog Cos Triangle Area For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. Areaδ = ½ ab sin c. We use the law. Cos Triangle Area.
From ontobel.com
Area Of A Triangle Trigonometry Formula Question Video Using Cos Triangle Area We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. Watch this video to learn how to calculate the area of a triangle. Areaδ = ½ ab sin c. Perhaps the most familiar formula for the area. Cosines, and area of triangles formulas, notes,. Cos Triangle Area.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Cos Triangle Area The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. Watch this video to learn how to calculate the area of a triangle. \ (\text {area of a triangle}. Cos Triangle Area.
From www.teachoo.com
Law of Cosine (Cosine Law) with Examples and Proof Teachoo Cos Triangle Area Watch this video to learn how to calculate the area of a triangle. Areaδ = ½ ab sin c. To be able to calculate the. We will now develop a few different ways to calculate the area of a triangle. The area of a triangle can be expressed using the lengths of two sides and the sine of the included. Cos Triangle Area.
From www.studypool.com
SOLUTION Sine rule cosine rule area of triangle Studypool Cos Triangle Area Perhaps the most familiar formula for the area. Areaδ = ½ ab sin c. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. The area of any triangle can be. Cos Triangle Area.
From online-learning-college.com
More trigonometry rules Sine & Cosine Rule Solving a Triangle Cos Triangle Area Areaδ = ½ ab sin c. To be able to calculate the. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles. Cos Triangle Area.
From nickolasknoeroy.blogspot.com
Area of Triangle Sine Rule NickolasknoeRoy Cos Triangle Area Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. Watch this video to learn how to calculate the area of a triangle. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. To be able to calculate the. The area. Cos Triangle Area.
From www.youtube.com
Q24 Cosine rule area triangle YouTube Cos Triangle Area The area of any triangle can be calculated using the formula: For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. Perhaps the most familiar formula for the area. To be able to calculate the. We will now develop. Cos Triangle Area.
From calcworkshop.com
What is the Law of Cosines? (Explained in 3 Powerful Examples!) Cos Triangle Area Watch this video to learn how to calculate the area of a triangle. Perhaps the most familiar formula for the area. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The area of any triangle can be calculated using the formula: We will now develop a few different. Cos Triangle Area.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Cos Triangle Area \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. Watch this video to learn how to calculate the area of a triangle. Perhaps the most familiar formula for the area. The area of a triangle can be expressed using the lengths of two sides and the sine of the included. Cos Triangle Area.
From www.teachoo.com
What are sin cos tan? SOHCAHTOA With Examples Teachoo Cos Triangle Area We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. For the triangle with side 10 we obtain area = 102 × √3 / 4 = 100 × √3 / 4 = 25 × √3, which is approximately equal to 43.3. Cosines, and area. Cos Triangle Area.
From www.youtube.com
How to use the Cosine Rule to find an Angle YouTube Cos Triangle Area To be able to calculate the. Areaδ = ½ ab sin c. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles and sides, the. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Watch this video to learn how to. Cos Triangle Area.
From hwtwom.blogspot.com
How To Find The Area Of A Triangle Cosine Rule howto Cos Triangle Area To be able to calculate the. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. Watch this video to learn how to calculate the area of a triangle. We will now develop a few different ways to calculate the area of a triangle.. Cos Triangle Area.
From www.youtube.com
Example Determine the Area of a Triangle Using the Sine Function YouTube Cos Triangle Area To be able to calculate the. The area of any triangle can be calculated using the formula: We will now develop a few different ways to calculate the area of a triangle. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Perhaps the most familiar formula for the. Cos Triangle Area.
From v-fedun.staff.shef.ac.uk
Trigonometry Cos Triangle Area To be able to calculate the. The area of any triangle can be calculated using the formula: We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. Cosines, and area of triangles formulas, notes, examples, and practice test (with solutions) topics include finding angles. Cos Triangle Area.
From healthy-food-near-me.com
Cosine theorem for a triangle formula and tasks Healthy Food Near Me Cos Triangle Area Areaδ = ½ ab sin c. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. Perhaps the most familiar formula for the area. To be able to calculate the. The area of any triangle can be calculated using the formula: \ (\text {area. Cos Triangle Area.
From www.youtube.com
P2 6 2 Law of Cosines Area of Triangles YouTube Cos Triangle Area \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate the area of any. We use the law of sines and law of cosines to “solve” triangles (find missing angles and sides) for oblique triangles (triangles that don’t have a. Watch this video to learn how to calculate the area of a triangle. For the. Cos Triangle Area.