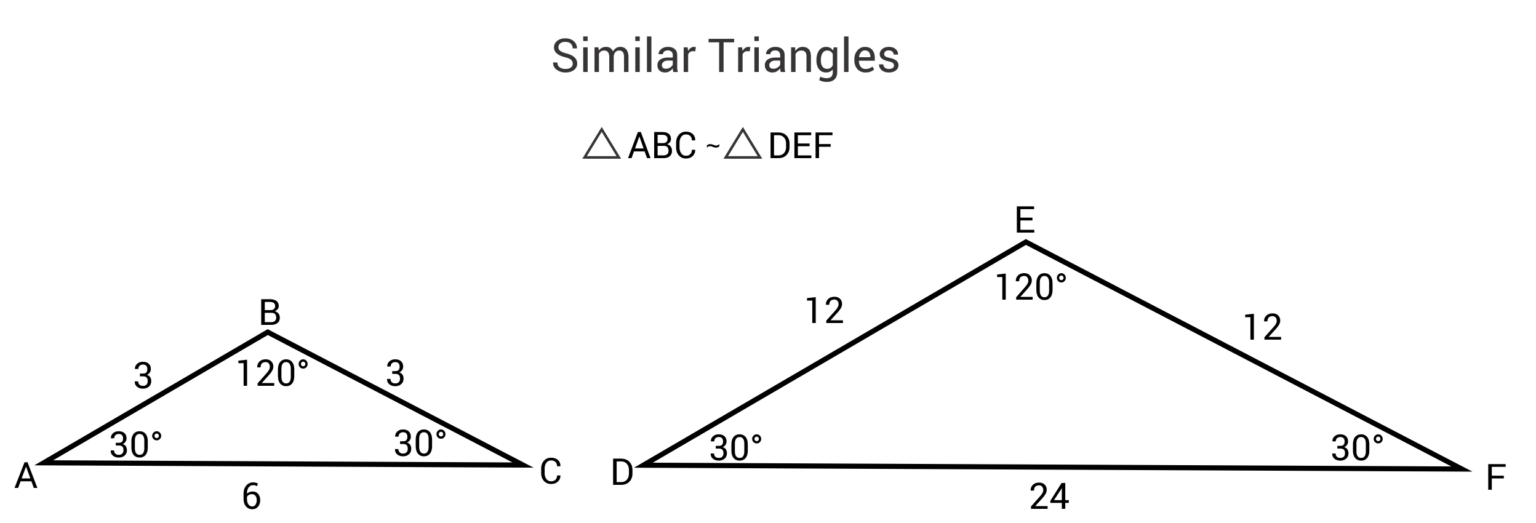
Triangles Are Similar Find X at Madison Wardell blog

Triangles Are Similar Find X. Prove similar triangles, given sides and angles. Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other. Triangles abc and pqr are similar and have sides in the ratio x:y. We can find the areas using this formula from area of a triangle: Ab/ef = bc/fg = ac/eg and ∠b ≅ ∠f. From the above figure with aa rule, we can write. It states that if two angles in one triangle are equal to two angles of the other triangle, then the two triangles are similar. This math video tutorial discusses similar triangles and how to use proportions to find the. Use this similar triangles calculator to check whether two triangles are similar or to find the missing length of a similar triangle. Area of abc = 12 bc sin(a) area of pqr = 12 qr. Understand the different theorems to prove. (equal angles have been marked with the same. These triangles are all similar: Two triangles are similar if the only difference is size (and possibly the need to turn or flip one around).

Two triangles are similar if the only difference is size (and possibly the need to turn or flip one around). We can find the areas using this formula from area of a triangle: Use this similar triangles calculator to check whether two triangles are similar or to find the missing length of a similar triangle. Understand the different theorems to prove. Ab/ef = bc/fg = ac/eg and ∠b ≅ ∠f. From the above figure with aa rule, we can write. Triangles abc and pqr are similar and have sides in the ratio x:y. This math video tutorial discusses similar triangles and how to use proportions to find the. It states that if two angles in one triangle are equal to two angles of the other triangle, then the two triangles are similar. Area of abc = 12 bc sin(a) area of pqr = 12 qr.

Properties of Similar Triangles Algebra Review (Video)

Triangles Are Similar Find X Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other. Use this similar triangles calculator to check whether two triangles are similar or to find the missing length of a similar triangle. It states that if two angles in one triangle are equal to two angles of the other triangle, then the two triangles are similar. Ab/ef = bc/fg = ac/eg and ∠b ≅ ∠f. Understand the different theorems to prove. Prove similar triangles, given sides and angles. Two triangles are similar if the only difference is size (and possibly the need to turn or flip one around). From the above figure with aa rule, we can write. These triangles are all similar: Triangles abc and pqr are similar and have sides in the ratio x:y. (equal angles have been marked with the same. This math video tutorial discusses similar triangles and how to use proportions to find the. Similar triangles are the triangles that have corresponding sides in proportion to each other and corresponding angles equal to each other. Area of abc = 12 bc sin(a) area of pqr = 12 qr. We can find the areas using this formula from area of a triangle: