Damped Vibration Differential Equation at Alexandra Connibere blog

Damped Vibration Differential Equation. It’s now time to look at the final vibration case. The expression for critical damping comes from the solution of the differential equation. A guitar string stops oscillating a few. We set up and solve (using complex exponentials) the equation of motion for a damped harmonic oscillator in the overdamped, underdamped and. The solution to the system differential equation is. You may have forgotten what a dashpot (or damper) does. This is the full blown case where we consider every last possible force that can act upon the system. In this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. (ii) solve the differential equation. When damping is present but there is no external force, the system. Let us rewrite the equation \[ mx'' + cx' + kx = 0 \nonumber \] as \[ x'' + 2px' + w^2_0x = 0. Let us now focus on damped motion. Free damped vibration ([asciimath]cgt0,\ f(t)=0[/asciimath]): (i) get a differential equation for s using f=ma.

We set up and solve (using complex exponentials) the equation of motion for a damped harmonic oscillator in the overdamped, underdamped and. Free damped vibration ([asciimath]cgt0,\ f(t)=0[/asciimath]): A guitar string stops oscillating a few. This is the full blown case where we consider every last possible force that can act upon the system. Let us rewrite the equation \[ mx'' + cx' + kx = 0 \nonumber \] as \[ x'' + 2px' + w^2_0x = 0. (i) get a differential equation for s using f=ma. (ii) solve the differential equation. The expression for critical damping comes from the solution of the differential equation. When damping is present but there is no external force, the system. It’s now time to look at the final vibration case.

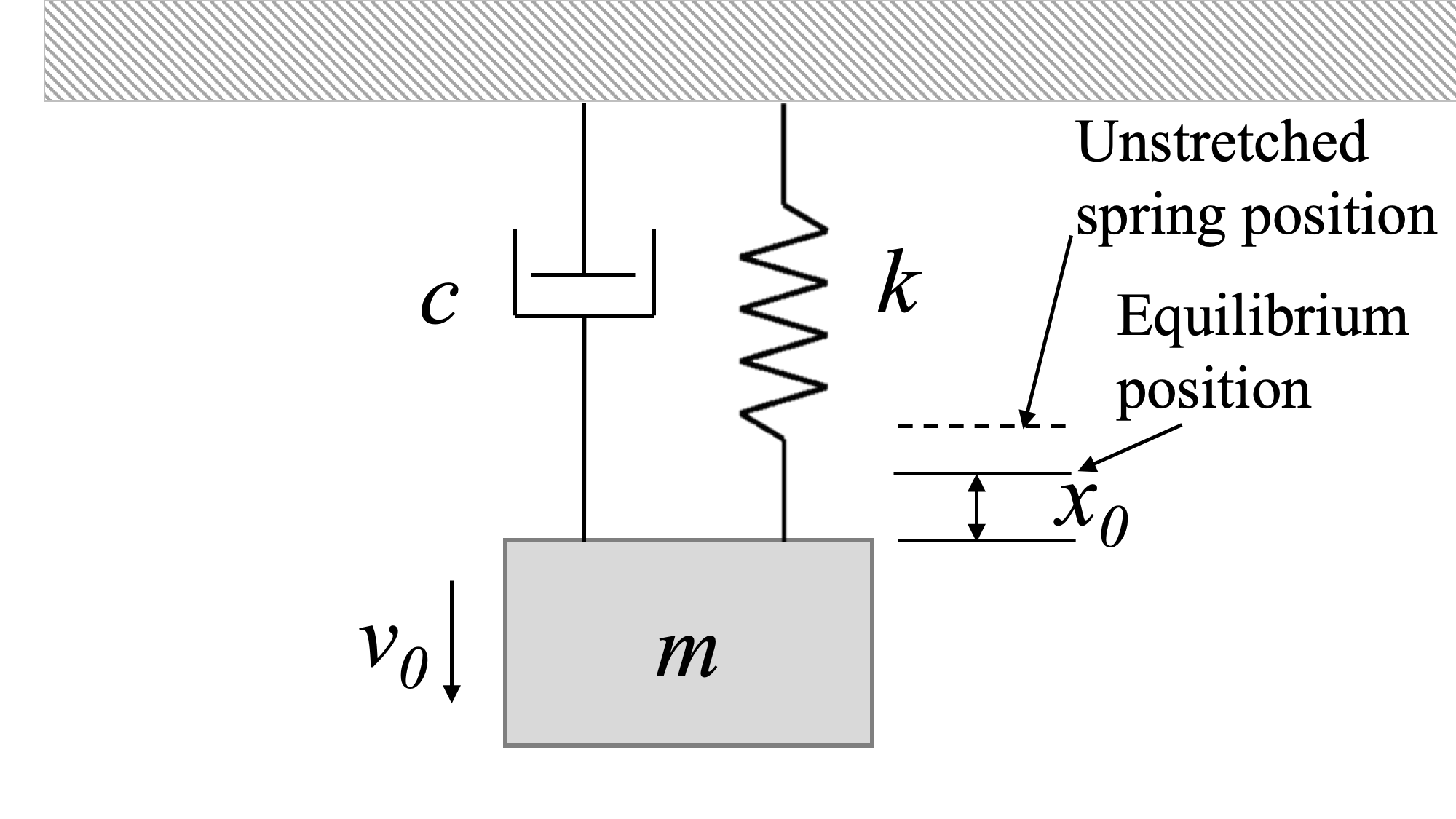
Mechanics Map Viscous Damped Free Vibrations

Damped Vibration Differential Equation The expression for critical damping comes from the solution of the differential equation. The expression for critical damping comes from the solution of the differential equation. A guitar string stops oscillating a few. (ii) solve the differential equation. It’s now time to look at the final vibration case. The solution to the system differential equation is. In this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to describe this more general case. (i) get a differential equation for s using f=ma. You may have forgotten what a dashpot (or damper) does. Let us now focus on damped motion. This is the full blown case where we consider every last possible force that can act upon the system. When damping is present but there is no external force, the system. Let us rewrite the equation \[ mx'' + cx' + kx = 0 \nonumber \] as \[ x'' + 2px' + w^2_0x = 0. Free damped vibration ([asciimath]cgt0,\ f(t)=0[/asciimath]): We set up and solve (using complex exponentials) the equation of motion for a damped harmonic oscillator in the overdamped, underdamped and.