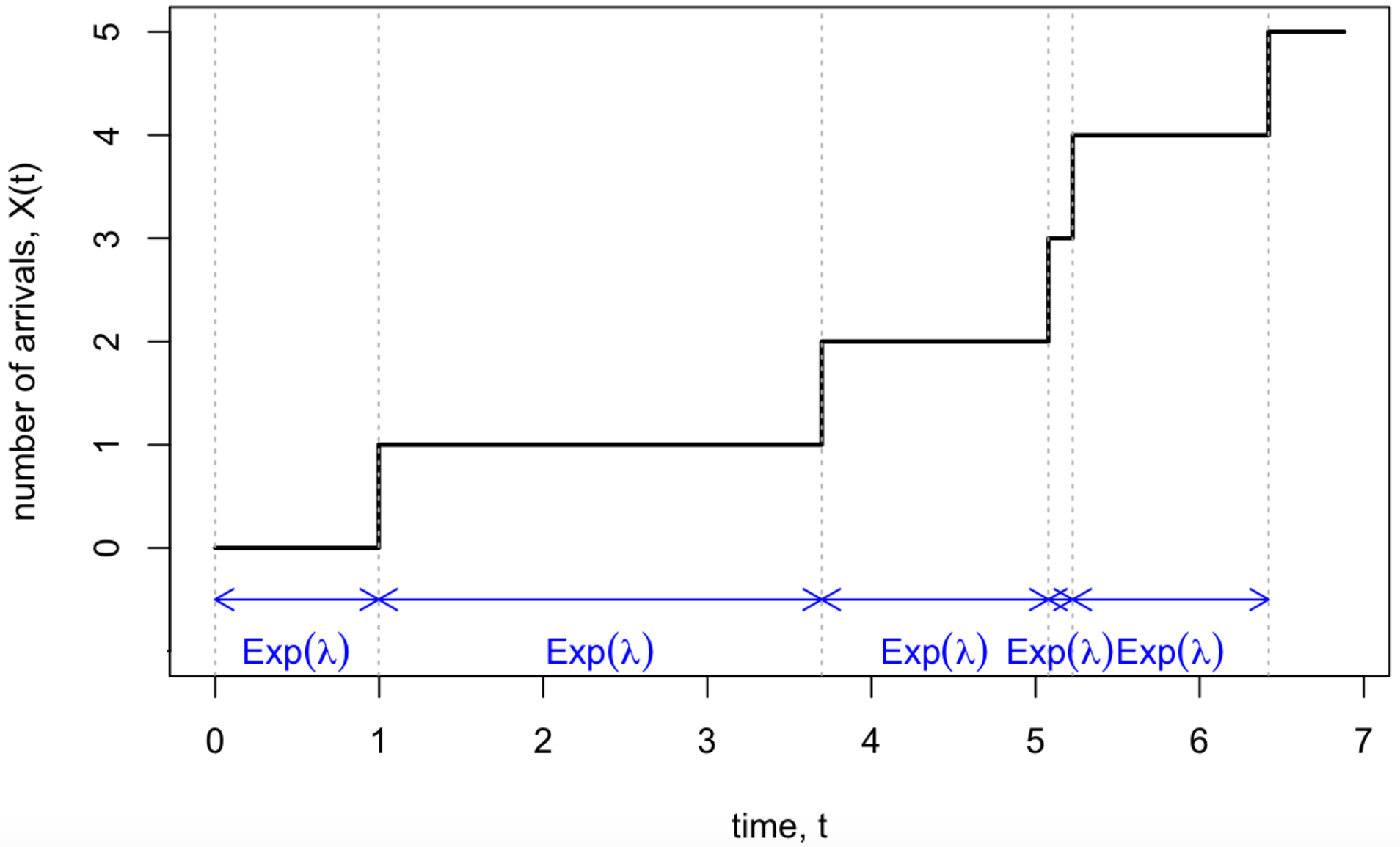
Poisson Process Interarrival Time Distribution at Luke Kara blog

Poisson Process Interarrival Time Distribution. The mean interarrival time for a poisson process is 1/λ. Let $n(t)$ be a poisson process with intensity $\lambda=2$, and let $x_1$, $x_2$, $\cdots$ be the corresponding interarrival times. The arrival times of events in a poisson process will be continuous random variables. A poisson process has poisson increments later, in section 1.6 we will prove the fundamental fact that: By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. Consider the times t1 and t2. In particular, the time between two successive events, say. The poisson process • readings: Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. But the mean time from any given t to the next arrival is 1/λ and the mean time.

Consider the times t1 and t2. The arrival times of events in a poisson process will be continuous random variables. The mean interarrival time for a poisson process is 1/λ. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. A poisson process has poisson increments later, in section 1.6 we will prove the fundamental fact that: In particular, the time between two successive events, say. But the mean time from any given t to the next arrival is 1/λ and the mean time. The poisson process • readings: Let $n(t)$ be a poisson process with intensity $\lambda=2$, and let $x_1$, $x_2$, $\cdots$ be the corresponding interarrival times. Lecture outline • review of bernoulli process • definition of poisson process • distribution of.

Section 14 Poisson process with exponential holding times MATH2750

Poisson Process Interarrival Time Distribution Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. The arrival times of events in a poisson process will be continuous random variables. The mean interarrival time for a poisson process is 1/λ. But the mean time from any given t to the next arrival is 1/λ and the mean time. Consider the times t1 and t2. The poisson process • readings: A poisson process has poisson increments later, in section 1.6 we will prove the fundamental fact that: Let $n(t)$ be a poisson process with intensity $\lambda=2$, and let $x_1$, $x_2$, $\cdots$ be the corresponding interarrival times. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. In particular, the time between two successive events, say.