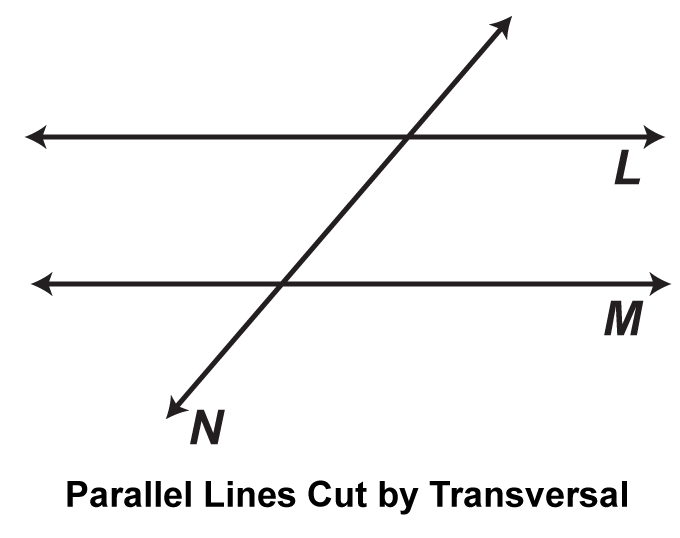
Lines J And K Are Parallel . \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. Show that \(k \nparallel n\). this problem involves the properties of parallel lines and the angles that they form. parallel lines are lines in the same plane that go in the same direction and never intersect. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. Since the lines j and k are. However, some authors allow a line to be. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. When a third line, called a. let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. parallel lines are lines that never intersect, and they form the same. Always the same distance apart and never.
from www.media4math.com
according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). However, some authors allow a line to be. When a third line, called a. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. Show that \(k \nparallel n\). if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. Since the lines j and k are. this problem involves the properties of parallel lines and the angles that they form. Always the same distance apart and never.
Student Tutorial Parallel Lines Cut by a Transversal Media4Math
Lines J And K Are Parallel Always the same distance apart and never. let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). Since the lines j and k are. parallel lines are lines that never intersect, and they form the same. if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. parallel lines are lines in the same plane that go in the same direction and never intersect. When a third line, called a. \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. Show that \(k \nparallel n\). Always the same distance apart and never. this problem involves the properties of parallel lines and the angles that they form. However, some authors allow a line to be. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often.
From brainly.in
5.2 In Fig. 29, j and k are parallel lines. Find the value of x. Give Lines J And K Are Parallel parallel lines are lines that never intersect, and they form the same. When a third line, called a. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. Show that \(k \nparallel n\). if parallel lines are cut by a transversal (a third line not parallel to the others), then. Lines J And K Are Parallel.
From brainly.com
Find the slope of lines k and j Lines J And K Are Parallel Since the lines j and k are. parallel lines are lines that never intersect, and they form the same. However, some authors allow a line to be. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. Show that \(k \nparallel n\). this problem involves the properties of parallel lines. Lines J And K Are Parallel.
From brainly.com
Lines j and k are parallel. Suppose m Lines J And K Are Parallel let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). parallel lines are lines in the same plane that go in the same direction and never intersect. Show that \(k \nparallel n\). according to the axioms of euclidean geometry, a line is not parallel to itself, since. Lines J And K Are Parallel.
From brainly.com
Parallel lines q and m are cut by transversal lines j and k. The lines Lines J And K Are Parallel When a third line, called a. Since the lines j and k are. if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). However, some authors allow a. Lines J And K Are Parallel.
From www.cuemath.com
Distance Formula Derivation, Examples All Distance Formulas in Maths Lines J And K Are Parallel Always the same distance apart and never. this problem involves the properties of parallel lines and the angles that they form. Show that \(k \nparallel n\). let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). parallel lines are lines that never intersect, and they form the. Lines J And K Are Parallel.
From www.cuemath.com
Lines in Geometry Types, Examples Geometric Lines Lines J And K Are Parallel lines are parallel if they are always the same distance apart (called equidistant), and will never meet. Show that \(k \nparallel n\). \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. parallel lines are lines that never intersect, and they form the same. if parallel lines are cut by a transversal (a third line not parallel. Lines J And K Are Parallel.
From www.slideserve.com
PPT Points, Lines, & Planes PowerPoint Presentation, free download Lines J And K Are Parallel \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. When a third line, called a. parallel lines are lines that never intersect, and they form the same. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. if parallel lines are cut by a transversal (a third line not. Lines J And K Are Parallel.
From brainly.com
in the diagram below,lines jk and lm are Lines J And K Are Parallel this problem involves the properties of parallel lines and the angles that they form. Show that \(k \nparallel n\). Always the same distance apart and never. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. Since the lines j and k are. parallel lines are lines that never intersect,. Lines J And K Are Parallel.
From www.youtube.com
Vectors Parallel YouTube Lines J And K Are Parallel Since the lines j and k are. if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\),. Lines J And K Are Parallel.
From brainly.in
In the following diagram, H I ‾ HI start overline, H, I, end overline Lines J And K Are Parallel Always the same distance apart and never. \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. Show that \(k \nparallel. Lines J And K Are Parallel.
From brainly.in
If the lines given by 3x+2ky=8 and 2x+5y4=0 are parallel , then find Lines J And K Are Parallel Always the same distance apart and never. When a third line, called a. if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. this problem involves the properties of parallel lines and the angles that they form. Show that \(k \nparallel n\). lines are parallel if they. Lines J And K Are Parallel.
From edurev.in
If two vectors 2i + 3j + k and 4i 6j λk are parallel to each Lines J And K Are Parallel Since the lines j and k are. let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. When a third line, called a. parallel lines are lines that never intersect, and they form the same. parallel lines. Lines J And K Are Parallel.
From brainly.com
100 POINTS!!!!! In this diagram, lines j and k are parallel. what are Lines J And K Are Parallel if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. parallel lines are lines in the same plane that go in the same direction and never intersect. However, some authors allow a line to be. Show that \(k \nparallel n\). lines are parallel if they are always. Lines J And K Are Parallel.
From www.chegg.com
Solved 40. In the figure, the horizontal lines are parallel Lines J And K Are Parallel However, some authors allow a line to be. Always the same distance apart and never. parallel lines are lines in the same plane that go in the same direction and never intersect. parallel lines are lines that never intersect, and they form the same. lines are parallel if they are always the same distance apart (called equidistant),. Lines J And K Are Parallel.
From brainly.com
In this diagram, lines j and k are parallel. Find values of x and y Lines J And K Are Parallel However, some authors allow a line to be. Since the lines j and k are. parallel lines are lines in the same plane that go in the same direction and never intersect. Always the same distance apart and never. this problem involves the properties of parallel lines and the angles that they form. parallel lines are lines. Lines J And K Are Parallel.
From brainly.com
in the figure the horizontal lines are parallel and ab=bc=cd if lm =5 Lines J And K Are Parallel lines are parallel if they are always the same distance apart (called equidistant), and will never meet. parallel lines are lines that never intersect, and they form the same. However, some authors allow a line to be. parallel lines are lines in the same plane that go in the same direction and never intersect. Always the same. Lines J And K Are Parallel.
From brainly.com
Line k is parallel to line l Lines J And K Are Parallel if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. Since the lines j and k are. \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. Always. Lines J And K Are Parallel.
From conversationcakesa.blogspot.com
Collinear Vectors Examples Lines J And K Are Parallel parallel lines are lines in the same plane that go in the same direction and never intersect. However, some authors allow a line to be. this problem involves the properties of parallel lines and the angles that they form. Since the lines j and k are. let \(k, \ell, m\), and \(n\) be lines such that \(k. Lines J And K Are Parallel.
From www.teachoo.com
If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, Lines J And K Are Parallel according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. Since the lines j and k are. parallel lines are lines in the same plane that go in the same direction and never intersect. When a third line, called a. if parallel lines are cut by a. Lines J And K Are Parallel.
From brainly.com
HELP 20 POINTS Lines j and k are shown in the diagram below. Some of Lines J And K Are Parallel if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. parallel lines are lines that never intersect, and they form the same. lines are parallel if they are always the same distance apart (called equidistant), and will. Lines J And K Are Parallel.
From en.asriportal.com
Points J and K are midpoints of the sides of triangle FGH. What is the Lines J And K Are Parallel When a third line, called a. parallel lines are lines in the same plane that go in the same direction and never intersect. parallel lines are lines that never intersect, and they form the same. Show that \(k \nparallel n\). lines are parallel if they are always the same distance apart (called equidistant), and will never meet.. Lines J And K Are Parallel.
From www.youtube.com
Vectors Prove that 2 vectors are parallel to each other YouTube Lines J And K Are Parallel parallel lines are lines in the same plane that go in the same direction and never intersect. When a third line, called a. \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. this problem involves the properties of parallel lines and the angles that they form. Show that \(k \nparallel n\). lines are parallel if they. Lines J And K Are Parallel.
From www.media4math.com
Student Tutorial Parallel Lines Cut by a Transversal Media4Math Lines J And K Are Parallel \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. Always the same distance apart and never. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). . Lines J And K Are Parallel.
From www.ck12.org
Proving Lines Parallel CK12 Foundation Lines J And K Are Parallel However, some authors allow a line to be. parallel lines are lines that never intersect, and they form the same. Always the same distance apart and never. When a third line, called a. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. let \(k, \ell, m\),. Lines J And K Are Parallel.
From brainly.com
In the figure shown below, lines j and k are parallel. Which equation Lines J And K Are Parallel Show that \(k \nparallel n\). When a third line, called a. if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. this problem involves the properties of. Lines J And K Are Parallel.
From millerdidettioners.blogspot.com
how to find intersection of two lines Miller Didettioners Lines J And K Are Parallel let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). However, some authors allow a line to be. if parallel lines are cut by a transversal (a third line not parallel to the others), then they are corresponding. Always the same distance apart and never. Since the lines. Lines J And K Are Parallel.
From brainly.com
Lines j and k are parallel and intersected by line e. What is the value Lines J And K Are Parallel let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). Since the lines j and k are. When a third line, called a. parallel lines are lines in the same plane that go in the same direction and never intersect. \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate. Lines J And K Are Parallel.
From brainly.com
Parallel lines j and k are cut by a transversal l. Which pair of angles Lines J And K Are Parallel Since the lines j and k are. When a third line, called a. Show that \(k \nparallel n\). let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). parallel lines are lines in the same plane that go in the same direction and never intersect. parallel lines. Lines J And K Are Parallel.
From brainly.com
In this diagram, lines j and k are parallel. find the values of x and y Lines J And K Are Parallel let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. Show that \(k \nparallel n\). parallel lines are lines that never intersect, and they form the same.. Lines J And K Are Parallel.
From brainly.com
100 POINTS!!! In this diagram, lines j and k are parallel. Find the Lines J And K Are Parallel let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). Always the same distance apart and never. However, some authors allow a line to be. parallel lines are lines in the same plane that go in the same direction and never intersect. parallel lines are lines that. Lines J And K Are Parallel.
From brainly.com
Line j and Line k are parallel lines that have been translated. The Lines J And K Are Parallel according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. \(\overleftrightarrow{ab} || \overleftrightarrow{cd}\) since the arrows indicate parallel lines. However, some authors allow a line to be. Since the lines j and k are. Always the same distance apart and never. When a third line, called a. . Lines J And K Are Parallel.
From www.chegg.com
Solved Lines j and k are parallel. They are intersected by Lines J And K Are Parallel let \(k, \ell, m\), and \(n\) be lines such that \(k \perp \ell\), \(\ell \perp m\), and \(m \perp n\). Always the same distance apart and never. When a third line, called a. However, some authors allow a line to be. Since the lines j and k are. this problem involves the properties of parallel lines and the. Lines J And K Are Parallel.
From slidetodoc.com
Terra Nova Practice Lesson 17 Angles Formed By Lines J And K Are Parallel according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. Always the same distance apart and never. this problem involves the properties of parallel lines and the angles that they form. parallel lines are lines that never intersect, and they form the same. parallel lines are. Lines J And K Are Parallel.
From brainly.com
If j and k are intersecting lines, A and B are points on j, and C and D Lines J And K Are Parallel Since the lines j and k are. However, some authors allow a line to be. parallel lines are lines that never intersect, and they form the same. lines are parallel if they are always the same distance apart (called equidistant), and will never meet. Always the same distance apart and never. Show that \(k \nparallel n\). this. Lines J And K Are Parallel.
From www.vrogue.co
The Diagram Shows How To Draw Lines That Are Parallel vrogue.co Lines J And K Are Parallel parallel lines are lines in the same plane that go in the same direction and never intersect. When a third line, called a. according to the axioms of euclidean geometry, a line is not parallel to itself, since it intersects itself infinitely often. However, some authors allow a line to be. lines are parallel if they are. Lines J And K Are Parallel.