Find Standard Basis Of Matrix . Then, the set of vectors is called the standard basis of. The standard basis is also often. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Each of the standard basis vectors has unit length: (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). Determine the action of a linear transformation. Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. Find the matrix of a linear transformation with respect to the standard basis. A standard basis, also called a.
from www.chegg.com
Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. Each of the standard basis vectors has unit length: Determine the action of a linear transformation. Then, the set of vectors is called the standard basis of. A standard basis, also called a. The standard basis is also often. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). Find the matrix of a linear transformation with respect to the standard basis. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =.
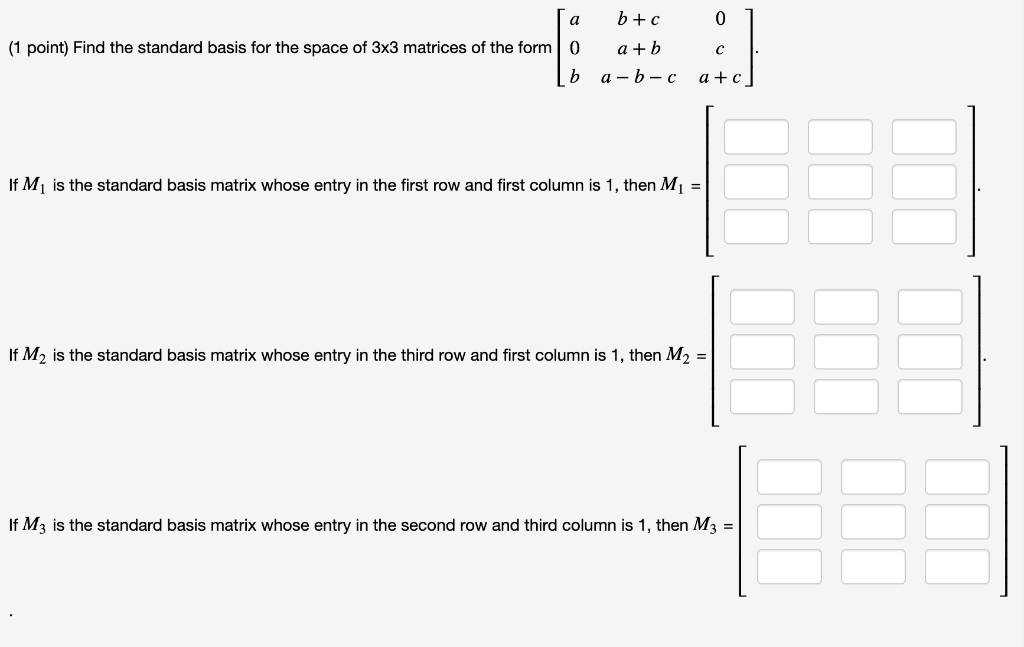
Solved [a (1 point) Find the standard basis for the space of
Find Standard Basis Of Matrix Find the matrix of a linear transformation with respect to the standard basis. Determine the action of a linear transformation. Each of the standard basis vectors has unit length: Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Then, the set of vectors is called the standard basis of. Find the matrix of a linear transformation with respect to the standard basis. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. A standard basis, also called a. The standard basis is also often. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors.
From www.youtube.com
How to Find the Matrix for a Linear Transformation Relative to Standard Find Standard Basis Of Matrix Each of the standard basis vectors has unit length: A standard basis, also called a. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Then, the set of vectors is called the standard basis of. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2. Find Standard Basis Of Matrix.
From www.numerade.com
Consider the ordered bases B = ((4,3), (1,1)) and C = ((0,2),(3,1 Find Standard Basis Of Matrix Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Each of the standard basis vectors has unit length: We need to find two vectors in \(\mathbb{r}^2. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVEDa. Find the change of basis matrix S from the basis B considered Find Standard Basis Of Matrix We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. A standard basis, also called a. Each of the standard basis vectors has unit length: Determine the action of a linear transformation. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. So one approach. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Find Standard Basis Of Matrix Then, the set of vectors is called the standard basis of. Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. A standard basis, also called a. The standard basis is also often. So one. Find Standard Basis Of Matrix.
From www.youtube.com
Use the Standard Basis to Find a Standard Matrix YouTube Find Standard Basis Of Matrix We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Then, the set of vectors is called the standard basis of. Determine the action of a linear transformation. Each of the standard basis vectors has unit length: Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$. Find Standard Basis Of Matrix.
From www.coursehero.com
[Solved] . Find the coordinate matrix of X relative to the standard Find Standard Basis Of Matrix (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. A standard basis, also called a. Write down the matrix. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVED Consider the ordered bases B = ((0,1), (1,1)) and C = ((2,2 Find Standard Basis Of Matrix Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. The standard basis is also often. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. A standard basis, also called a. Then, the set of vectors is called the standard basis of. Determine the. Find Standard Basis Of Matrix.
From www.chegg.com
Solved (1 pt) Find the matrix A of the linear transformation Find Standard Basis Of Matrix A standard basis, also called a. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Find the matrix of a linear transformation with respect to the standard basis. (1) for example, in the euclidean plane r^2, the. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVEDa. Find the change of basis matrix S from the basis 2 considered Find Standard Basis Of Matrix We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Determine the action of a linear transformation. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. Then, the set of vectors is called the standard basis of. Each of the standard basis vectors has. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVED Consider the matrix Find a basis of the orthogonal complement Find Standard Basis Of Matrix Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Find the matrix of a linear transformation with respect to the standard basis. Each of the standard basis vectors has unit length: (1) for example,. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVED Given the coordinate matrix of x relative to (nonstandard Find Standard Basis Of Matrix Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. Find the matrix of a linear transformation with respect to the standard basis. The standard basis is also often. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. We need to find two. Find Standard Basis Of Matrix.
From www.youtube.com
Tutorial Q78 Basis in vector space of 2x2 matrices YouTube Find Standard Basis Of Matrix Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). Each of the standard basis vectors has unit length: Find the matrix of a linear transformation with respect to the standard basis. (1) for example, in the euclidean plane r^2, the standard basis is e_1. Find Standard Basis Of Matrix.
From www.youtube.com
Matrix with respect to a basis YouTube Find Standard Basis Of Matrix A standard basis, also called a. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. (1) for example, in the euclidean plane r^2, the standard basis is. Find Standard Basis Of Matrix.
From www.coursehero.com
[Solved] Find the standard matrix of the linear transformation Find Standard Basis Of Matrix Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your. Find Standard Basis Of Matrix.
From www.youtube.com
The Standard Basis of a General Linear Transformation YouTube Find Standard Basis Of Matrix A standard basis, also called a. Find the matrix of a linear transformation with respect to the standard basis. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Then, the set of vectors is called the standard basis of. One such basis is \(\bigl\{{1\choose. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Let epsilon be the standard basis for R^3, and let B Find Standard Basis Of Matrix So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. Find the matrix of a linear transformation with respect to. Find Standard Basis Of Matrix.
From www.youtube.com
Linear Algebra Example Problems Matrix Null Space Basis and Dimension Find Standard Basis Of Matrix A standard basis, also called a. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). Determine the action of a linear transformation. Then, the set of vectors is called the standard basis of. The standard basis is also often. Each of the standard basis. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Find a basis for the column space of the matrix. 1 Find Standard Basis Of Matrix We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors.. Find Standard Basis Of Matrix.
From www.pinterest.com
Linear Transformation Standard Matrix & The Standard Basis Find Standard Basis Of Matrix We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Each of the standard basis vectors has unit length: Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. So one approach would be to solve a system of linear equations to write the vectors. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVEDa. Find the change of basis matrix S from the basis Y considered Find Standard Basis Of Matrix So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Find the matrix of a linear transformation with respect to the standard basis. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. One such basis is. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Find the change of basis matrix from the standard Find Standard Basis Of Matrix So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Determine the action of a linear transformation. A standard basis, also called a. Find the matrix of a linear transformation with respect to the standard basis. The standard basis is also often. Each of the. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Find the change of basis matrix from the standard Find Standard Basis Of Matrix Find the matrix of a linear transformation with respect to the standard basis. Then, the set of vectors is called the standard basis of. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). The standard basis is also often. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Determine the action of a linear. Find Standard Basis Of Matrix.
From www.youtube.com
Matrix Representation standard ordered Basis linear transformation T(5 Find Standard Basis Of Matrix A standard basis, also called a. Find the matrix of a linear transformation with respect to the standard basis. The standard basis is also often. Each of the standard basis vectors has unit length: So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Determine. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVED (1 point) The set [ ][ ][ ] is called the standard basis Find Standard Basis Of Matrix (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. Each of the standard basis vectors has unit length: A standard basis, also called a. The standard basis is also often. Find the matrix of a linear transformation with respect to the standard basis. Then, the set of vectors is called the. Find Standard Basis Of Matrix.
From www.coursehero.com
[Solved] Find the changeofcoordinates matrix from B to the standard Find Standard Basis Of Matrix Determine the action of a linear transformation. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. Then, the set of vectors is called the standard basis. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Suppose A is the matrix for TR3→R3 relative to the Find Standard Basis Of Matrix Then, the set of vectors is called the standard basis of. Determine the action of a linear transformation. A standard basis, also called a. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Find the matrix of a linear transformation with respect to the standard basis. One such basis is \(\bigl\{{1\choose 0},{0\choose. Find Standard Basis Of Matrix.
From www.chegg.com
Solved [a (1 point) Find the standard basis for the space of Find Standard Basis Of Matrix Then, the set of vectors is called the standard basis of. Find the matrix of a linear transformation with respect to the standard basis. A standard basis, also called a. Determine the action of a linear transformation. Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. The standard basis is also. Find Standard Basis Of Matrix.
From www.chegg.com
Solved (1 point) The set is called the standard basis of the Find Standard Basis Of Matrix So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$. A standard basis, also called a. Find the matrix of a linear transformation with respect to the. Find Standard Basis Of Matrix.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free Find Standard Basis Of Matrix We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. The standard basis is also often. Find the matrix of a linear transformation with respect to the standard basis. Then, the set of vectors is called the standard basis of. So one approach would be to solve a system of linear equations to. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Let Be The Standard Basis In R2 And Be Another Bas... Find Standard Basis Of Matrix So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Determine the action of a linear transformation. Each of the standard basis vectors has unit length: A standard. Find Standard Basis Of Matrix.
From www.youtube.com
Finding a Standard Matrix Using the Standard Basis YouTube Find Standard Basis Of Matrix Then, the set of vectors is called the standard basis of. Determine the action of a linear transformation. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. Find the matrix of a linear transformation with respect to the standard basis. Write down the matrix of a of $\phi$ with respect to. Find Standard Basis Of Matrix.
From www.chegg.com
Solved The standard basis S={e1,e2} and a custom basis Find Standard Basis Of Matrix We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. So one approach would be to solve a system of linear equations to write the vectors of the standard basis in terms of your vectors. Write down the matrix of a of $\phi$ with respect to the standard bases of $\mathbb{r}^4$ and $\mathbb{r}^3$.. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Find a basis for the column space of the matrix. Let Find Standard Basis Of Matrix Each of the standard basis vectors has unit length: Find the matrix of a linear transformation with respect to the standard basis. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Then, the set of vectors is called the standard basis of. Write down the matrix of a of $\phi$ with respect. Find Standard Basis Of Matrix.
From www.numerade.com
SOLVED matrix representing that is similar to the Find the matrix Find Standard Basis Of Matrix The standard basis is also often. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. A standard basis, also called a. (1) for example, in the euclidean plane r^2, the standard basis is e_1 = e_x=(1,0) (2) e_2 =. One such basis is \(\bigl\{{1\choose 0},{0\choose 1}\bigr\}\text{:}\). Find the matrix of a linear. Find Standard Basis Of Matrix.
From www.chegg.com
Solved Consider the ordered bases B={ and C [1] (4) (1[6]} Find Standard Basis Of Matrix Then, the set of vectors is called the standard basis of. We need to find two vectors in \(\mathbb{r}^2 \) that span \(\mathbb{r}^2 \) and are linearly independent. Each of the standard basis vectors has unit length: The standard basis is also often. Find the matrix of a linear transformation with respect to the standard basis. (1) for example, in. Find Standard Basis Of Matrix.