Differential Geometry Vector Field . differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students.
from www.chegg.com
spaces, submanifolds and embeddings, and vector. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students.
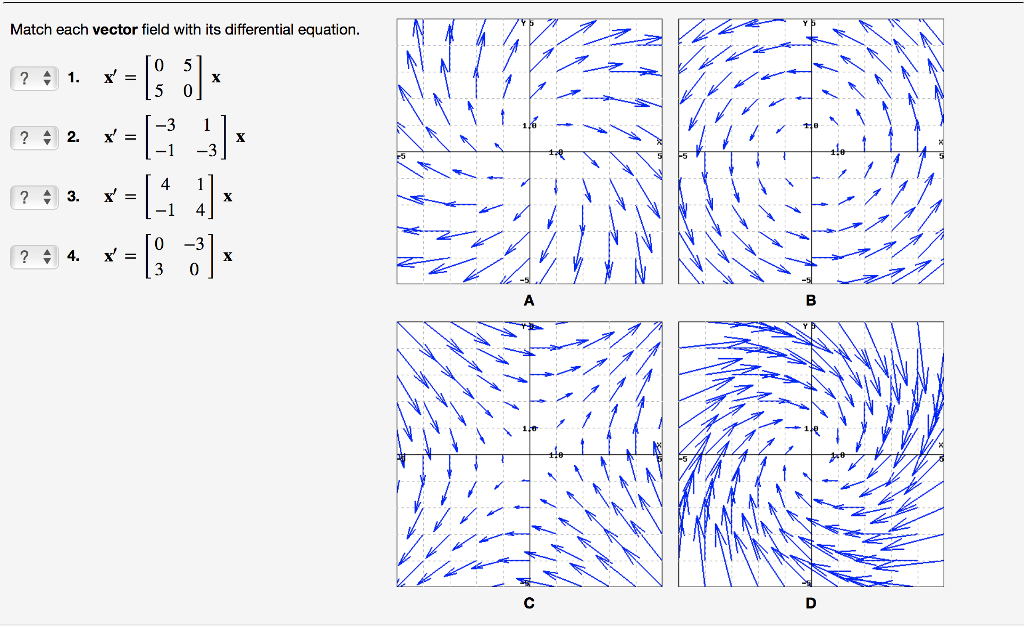
Solved Match each vector field with its differential
Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi.
From demonstrations.wolfram.com
Direction Fields for Differential Equations Wolfram Demonstrations Differential Geometry Vector Field spaces, submanifolds and embeddings, and vector. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. the important property of vector fields which. Differential Geometry Vector Field.
From www.youtube.com
Vector Field System Differential Equations YouTube Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. this textbook serves as an introduction to modern differential geometry at a level accessible. Differential Geometry Vector Field.
From www.youtube.com
Differential Equations Direction Fields Example 1 YouTube Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. . Differential Geometry Vector Field.
From www.researchgate.net
The vector field of the differential system (15) and its equilibria Differential Geometry Vector Field this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. differential forms as well, it is will be necessary to take shortcuts with some of the. Differential Geometry Vector Field.
From math.stackexchange.com
differential geometry Finding tangent vectors to unit circle Differential Geometry Vector Field the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. spaces, submanifolds and embeddings, and vector. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. a differential form is a linear transformation from the vector fields to the reals. Differential Geometry Vector Field.
From vectorified.com
2d Vector Field Grapher at Collection of 2d Vector Differential Geometry Vector Field spaces, submanifolds and embeddings, and vector. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. this textbook serves as an introduction to modern differential geometry at a level accessible. Differential Geometry Vector Field.
From www.amazon.ca
Manifolds, Vector Fields, and Differential Forms An Introduction to Differential Geometry Vector Field differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. spaces, submanifolds and embeddings, and vector. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. this textbook serves as an introduction to. Differential Geometry Vector Field.
From www.researchgate.net
(PDF) Differential geometry of position vector fields of Euclidean Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by. Differential Geometry Vector Field.
From www.researchgate.net
Can I plot the vector field for system of ordinary differential equations? Differential Geometry Vector Field differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. the important property of vector fields which we are interested in is that they act as derivations of the algebra of. Differential Geometry Vector Field.
From www.youtube.com
Utilitarian Differential Geometry 2 Vector Fields YouTube Differential Geometry Vector Field a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. spaces, submanifolds and embeddings, and vector. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. differential forms as well, it is will be necessary to take shortcuts with some of. Differential Geometry Vector Field.
From math.stackexchange.com
differential geometry geometric interpretation on covariant Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act. Differential Geometry Vector Field.
From mathinsight.org
The idea of the curl of a vector field Math Insight Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. a differential form is a linear transformation from the vector fields to the reals. Differential Geometry Vector Field.
From brickisland.net
Supplemental VectorValued Differential Forms CS 15458/858 Differential Geometry Vector Field differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. a differential form is a linear. Differential Geometry Vector Field.
From www.researchgate.net
Vector field plots of differential equations (2), (3) and (4 Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. . Differential Geometry Vector Field.
From www.slideserve.com
PPT Introduction to General Relativity PowerPoint Presentation, free Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. . Differential Geometry Vector Field.
From www.youtube.com
Lecture 5 Differential Forms (Discrete Differential Geometry) YouTube Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi.. Differential Geometry Vector Field.
From www.researchgate.net
Geometry of tangent vector field Download Scientific Diagram Differential Geometry Vector Field a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. differential forms as well, it is will be necessary to take shortcuts with some. Differential Geometry Vector Field.
From www.youtube.com
Lecture 12 Directional Fields Differential Equations YouTube Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. spaces, submanifolds and embeddings, and vector. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. the important property of vector fields which we are interested in is that they act as. Differential Geometry Vector Field.
From faculty.cooper.edu
Differential Geometry miscellaneous resources Differential Geometry Vector Field spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. this textbook serves as an introduction to modern differential geometry at a level accessible. Differential Geometry Vector Field.
From www.chegg.com
Solved Match each vector field with its differential Differential Geometry Vector Field a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending.. Differential Geometry Vector Field.
From socratic.org
Differential equation vector field for dy/dx = (x + 1) (y + 1) (1 y Differential Geometry Vector Field a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. this textbook serves as an introduction to modern differential geometry at a level accessible. Differential Geometry Vector Field.
From math.stackexchange.com
differential geometry Geometric interpretation of the Lie bracket Differential Geometry Vector Field this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. . Differential Geometry Vector Field.
From pdfprof.com
a constant vector field Differential Geometry Vector Field this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. spaces, submanifolds and embeddings, and vector. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we. Differential Geometry Vector Field.
From www.researchgate.net
(PDF) Classification of Holomorphic Functions as Pólya Vector Fields Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. spaces, submanifolds and embeddings, and vector. a differential form is a linear transformation from the vector fields to the reals. Differential Geometry Vector Field.
From www.researchgate.net
(PDF) Differential Geometry and Relativity Theories vol 1. Tangent Differential Geometry Vector Field the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. spaces, submanifolds and embeddings, and vector. for any element \({\boldsymbol{a}} \in \mathfrak. Differential Geometry Vector Field.
From www.chegg.com
Solved Match each vector field with its differential Differential Geometry Vector Field differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. the important property of vector fields which we are interested in is that they act. Differential Geometry Vector Field.
From www.youtube.com
Differential Equations Direction Fields Introduction YouTube Differential Geometry Vector Field the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi.. Differential Geometry Vector Field.
From math.stackexchange.com
differential geometry Vector Bundle Connection and Agreement a on Differential Geometry Vector Field this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. the important property of vector fields which we are interested in is that they act. Differential Geometry Vector Field.
From demonstrations.wolfram.com
Slope Field and Solutions of a Differential Equation Differential Geometry Vector Field differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. the important property of vector fields which we are interested in is that they. Differential Geometry Vector Field.
From mathinsight.org
Vector field overview Math Insight Differential Geometry Vector Field the important property of vector fields which we are interested in is that they act as derivations of the algebra of smooth. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. spaces, submanifolds and embeddings, and vector. for any element \({\boldsymbol{a}} \in \mathfrak. Differential Geometry Vector Field.
From brickisland.net
CS 15458/858 Discrete Differential Geometry CARNEGIE MELLON Differential Geometry Vector Field this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. differential forms as well, it is will be necessary to take shortcuts with some of the. Differential Geometry Vector Field.
From www.youtube.com
Lesson 6 Vector Fields & Differential Equations (Part 2) YouTube Differential Geometry Vector Field this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. a differential form is a linear transformation from the vector fields to the reals given. Differential Geometry Vector Field.
From www.researchgate.net
(PDF) Principles of Differential Geometry Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. spaces, submanifolds and embeddings, and vector. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. differential forms as well, it is will be necessary to take shortcuts with some of the. Differential Geometry Vector Field.
From www.youtube.com
Differential Equation with Vector Valued Function YouTube Differential Geometry Vector Field differential forms as well, it is will be necessary to take shortcuts with some of the earlier material, for example by spending. for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. . Differential Geometry Vector Field.
From www.youtube.com
Differential Geometry Video03Vector Fields YouTube Differential Geometry Vector Field for any element \({\boldsymbol{a}} \in \mathfrak {g}\) we can construct a fundamental vector field. this textbook serves as an introduction to modern differential geometry at a level accessible to advanced undergraduate and master's students. a differential form is a linear transformation from the vector fields to the reals given by α = xn i=1 aidxi. spaces,. Differential Geometry Vector Field.