Arc Length Vs Radius . Finally, multiply that number by 2 × pi. An arclength equal to one radius determines. Then the arc length \(s \) is: Arc length is a measurement of distance along the circumference of a circle or sector between. To find arc length, start by dividing the arc's central angle in degrees by 360. L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. Find the arc length of a sector by entering the central angle and radius in the calculator below. \[ s ~=~ r\,\theta \label{4.4} \] Then, multiply that number by the radius of the circle. In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure \(\theta \ge 0 \). We see that an angle of one radian spans an arc whose length is the radius of the circle. This is true for a circle of any size, as illustrated at right: The length of an arc depends on the radius of a circle and the central angle θ.
from owlcation.com
This is true for a circle of any size, as illustrated at right: The length of an arc depends on the radius of a circle and the central angle θ. Then the arc length \(s \) is: Then, multiply that number by the radius of the circle. We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. Finally, multiply that number by 2 × pi. Arc length is a measurement of distance along the circumference of a circle or sector between. L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) To find arc length, start by dividing the arc's central angle in degrees by 360. \[ s ~=~ r\,\theta \label{4.4} \]
How to Calculate Arc Length of a Circle, Segment and Sector Area
Arc Length Vs Radius An arclength equal to one radius determines. The length of an arc depends on the radius of a circle and the central angle θ. \[ s ~=~ r\,\theta \label{4.4} \] This is true for a circle of any size, as illustrated at right: Arc length is a measurement of distance along the circumference of a circle or sector between. We see that an angle of one radian spans an arc whose length is the radius of the circle. Find the arc length of a sector by entering the central angle and radius in the calculator below. Then the arc length \(s \) is: Finally, multiply that number by 2 × pi. Then, multiply that number by the radius of the circle. An arclength equal to one radius determines. To find arc length, start by dividing the arc's central angle in degrees by 360. L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure \(\theta \ge 0 \).
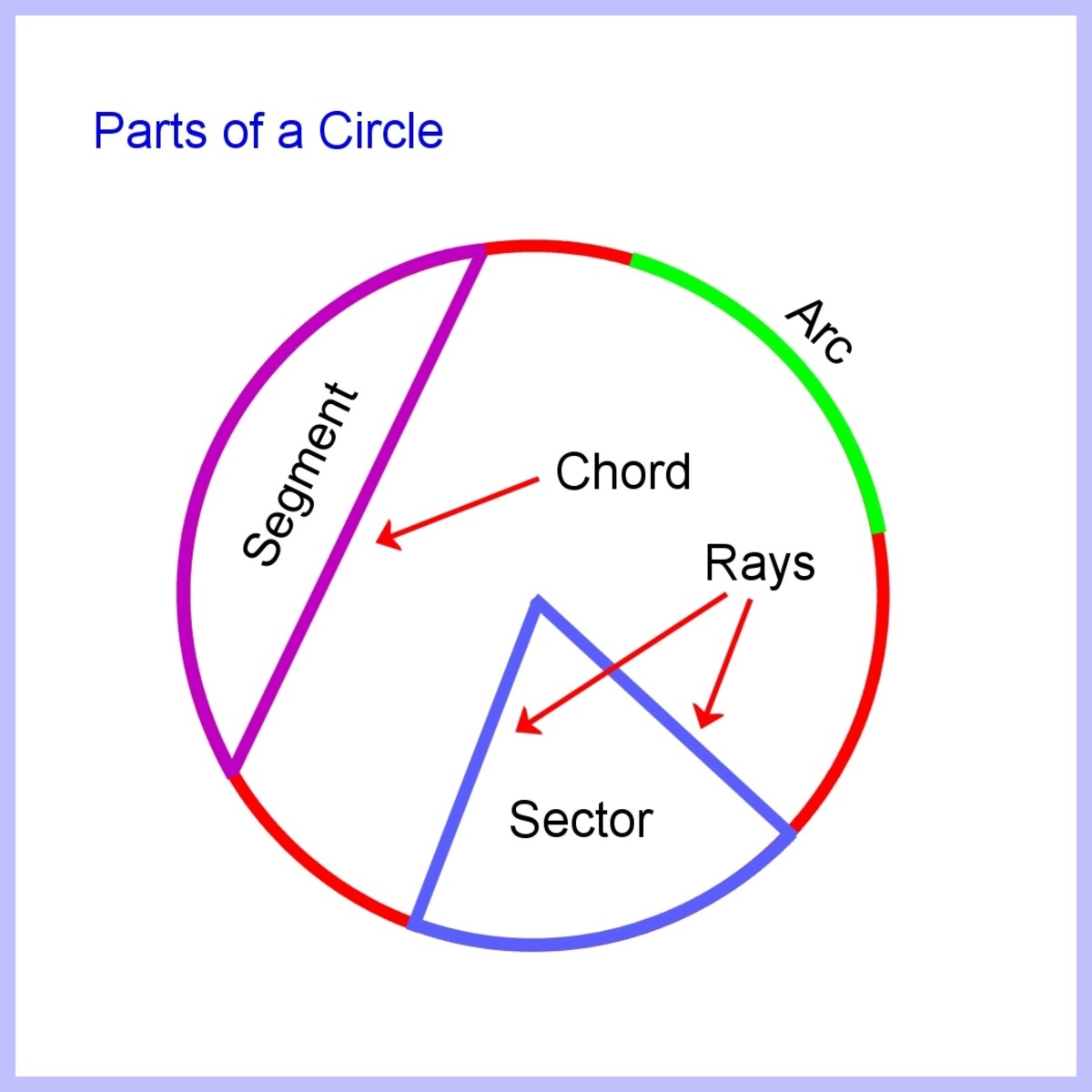
From mungfali.com
Length Of An Arc Formula Using Radians Teachoo Arc Length A88 Arc Length Vs Radius Then, multiply that number by the radius of the circle. Arc length is a measurement of distance along the circumference of a circle or sector between. We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. L = θ × r (when θ is in radians) l = θ × π 180. Arc Length Vs Radius.
From www.vcalc.com
Chord from Arc Length and Radius Arc Length Vs Radius Find the arc length of a sector by entering the central angle and radius in the calculator below. An arclength equal to one radius determines. To find arc length, start by dividing the arc's central angle in degrees by 360. Arc length is a measurement of distance along the circumference of a circle or sector between. The length of an. Arc Length Vs Radius.
From owlcation.com
How to Calculate Arc Length of a Circle, Segment and Sector Area Arc Length Vs Radius To find arc length, start by dividing the arc's central angle in degrees by 360. \[ s ~=~ r\,\theta \label{4.4} \] L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) In a circle of radius \(r \), let \(s \) be the length of an arc. Arc Length Vs Radius.
From www.numerade.com
In Exercises 97100, use the given arc length and radius to find the Arc Length Vs Radius Arc length is a measurement of distance along the circumference of a circle or sector between. The length of an arc depends on the radius of a circle and the central angle θ. An arclength equal to one radius determines. Then, multiply that number by the radius of the circle. Finally, multiply that number by 2 × pi. In a. Arc Length Vs Radius.
From owlcation.com
How to Calculate Arc Length of a Circle, Segment and Sector Area Arc Length Vs Radius \[ s ~=~ r\,\theta \label{4.4} \] Arc length is a measurement of distance along the circumference of a circle or sector between. Then the arc length \(s \) is: An arclength equal to one radius determines. Find the arc length of a sector by entering the central angle and radius in the calculator below. Then, multiply that number by the. Arc Length Vs Radius.
From www.tessshebaylo.com
Equation For Radius Of An Arc Tessshebaylo Arc Length Vs Radius An arclength equal to one radius determines. Then, multiply that number by the radius of the circle. Then the arc length \(s \) is: Finally, multiply that number by 2 × pi. We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. Find the arc length of a sector by entering the. Arc Length Vs Radius.
From magoosh.com
New SAT Math Circle Arc Length Magoosh High School Blog Arc Length Vs Radius Then the arc length \(s \) is: This is true for a circle of any size, as illustrated at right: L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) We know that for the angle equal to 360 degrees (2π), the arc length is equal to. Arc Length Vs Radius.
From thirdspacelearning.com
Arc Length GCSE Maths Steps, Examples & Worksheet Arc Length Vs Radius The length of an arc depends on the radius of a circle and the central angle θ. Find the arc length of a sector by entering the central angle and radius in the calculator below. Then, multiply that number by the radius of the circle. L = θ × r (when θ is in radians) l = θ × π. Arc Length Vs Radius.
From www.slideserve.com
PPT Arc Length PowerPoint Presentation, free download ID4881081 Arc Length Vs Radius We see that an angle of one radian spans an arc whose length is the radius of the circle. \[ s ~=~ r\,\theta \label{4.4} \] To find arc length, start by dividing the arc's central angle in degrees by 360. In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central. Arc Length Vs Radius.
From www.youtube.com
Finding Radius Given Arc Length and Angle Measure YouTube Arc Length Vs Radius L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) Arc length is a measurement of distance along the circumference of a circle or sector between. This is true for a circle of any size, as illustrated at right: In a circle of radius \(r \), let. Arc Length Vs Radius.
From study.com
How to Find Arc Length in Radians Geometry Arc Length Vs Radius Then the arc length \(s \) is: An arclength equal to one radius determines. Arc length is a measurement of distance along the circumference of a circle or sector between. \[ s ~=~ r\,\theta \label{4.4} \] In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure. Arc Length Vs Radius.
From owlcation.com
How to Calculate Arc Length of a Circle, Segment and Sector Area Arc Length Vs Radius L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) \[ s ~=~ r\,\theta \label{4.4} \] Finally, multiply that number by 2 × pi. Find the arc length of a sector by entering the central angle and radius in the calculator below. We know that for the. Arc Length Vs Radius.
From www.nagwa.com
Question Video Calculating the Measure of an Arc in Degrees given Its Arc Length Vs Radius Finally, multiply that number by 2 × pi. We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure \(\theta \ge 0 \). We see that an angle of. Arc Length Vs Radius.
From www.researchgate.net
Sagitta, arc length, chord length, and circle radius relationship Arc Length Vs Radius The length of an arc depends on the radius of a circle and the central angle θ. We see that an angle of one radian spans an arc whose length is the radius of the circle. Then the arc length \(s \) is: This is true for a circle of any size, as illustrated at right: In a circle of. Arc Length Vs Radius.
From owlcation.com
How to Calculate Arc Length of a Circle, Segment and Sector Area Arc Length Vs Radius Then the arc length \(s \) is: L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) \[ s ~=~ r\,\theta \label{4.4} \] We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. Find the arc length of a. Arc Length Vs Radius.
From www.learntocalculate.com
How to Calculate Radius of an Arc. Arc Length Vs Radius Find the arc length of a sector by entering the central angle and radius in the calculator below. Then, multiply that number by the radius of the circle. This is true for a circle of any size, as illustrated at right: An arclength equal to one radius determines. The length of an arc depends on the radius of a circle. Arc Length Vs Radius.
From brunofuga.adv.br
ARC Length Formula And Details Surveying Architects, 49 OFF Arc Length Vs Radius Then the arc length \(s \) is: An arclength equal to one radius determines. Find the arc length of a sector by entering the central angle and radius in the calculator below. This is true for a circle of any size, as illustrated at right: Then, multiply that number by the radius of the circle. The length of an arc. Arc Length Vs Radius.
From www.cuemath.com
What is a Radian? Cuemath Arc Length Vs Radius L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) Arc length is a measurement of distance along the circumference of a circle or sector between. Find the arc length of a sector by entering the central angle and radius in the calculator below. This is true. Arc Length Vs Radius.
From hubpages.com
Arc Length Calculation Given Only the Chord Length and Arc Height Arc Length Vs Radius Find the arc length of a sector by entering the central angle and radius in the calculator below. L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) Finally, multiply that number by 2 × pi. Then, multiply that number by the radius of the circle. In. Arc Length Vs Radius.
From mathbooks.unl.edu
MFG Arc Length Arc Length Vs Radius We know that for the angle equal to 360 degrees (2π), the arc length is equal to circumference. In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure \(\theta \ge 0 \). The length of an arc depends on the radius of a circle and the. Arc Length Vs Radius.
From www.youtube.com
Online Arc Calculator for Arc Length, Radius, Cord, Depth, Angle Arc Length Vs Radius Finally, multiply that number by 2 × pi. The length of an arc depends on the radius of a circle and the central angle θ. \[ s ~=~ r\,\theta \label{4.4} \] L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) We see that an angle of. Arc Length Vs Radius.
From www.youtube.com
Arc Length of a Circle Formula Sector Area, Examples, Radians, In Arc Length Vs Radius The length of an arc depends on the radius of a circle and the central angle θ. \[ s ~=~ r\,\theta \label{4.4} \] We see that an angle of one radian spans an arc whose length is the radius of the circle. L = θ × r (when θ is in radians) l = θ × π 180 × r. Arc Length Vs Radius.
From www.cuemath.com
Arc Length Formula, How to Find Length of an Arc Arc of a Circle Arc Length Vs Radius This is true for a circle of any size, as illustrated at right: Arc length is a measurement of distance along the circumference of a circle or sector between. In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by a central angle with radian measure \(\theta \ge 0 \). L = θ. Arc Length Vs Radius.
From www.youtube.com
When given the radius and angle, learn how to find the arc length YouTube Arc Length Vs Radius An arclength equal to one radius determines. Arc length is a measurement of distance along the circumference of a circle or sector between. L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) This is true for a circle of any size, as illustrated at right: Finally,. Arc Length Vs Radius.
From www.geogebra.org
Arc Length = Circle Radius x Angle GeoGebra Arc Length Vs Radius L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) We see that an angle of one radian spans an arc whose length is the radius of the circle. Arc length is a measurement of distance along the circumference of a circle or sector between. \[ s. Arc Length Vs Radius.
From calcworkshop.com
How to Find Arc Length? (Easily Explained with 5 Examples!) Arc Length Vs Radius An arclength equal to one radius determines. The length of an arc depends on the radius of a circle and the central angle θ. Arc length is a measurement of distance along the circumference of a circle or sector between. We see that an angle of one radian spans an arc whose length is the radius of the circle. To. Arc Length Vs Radius.
From www.inchcalculator.com
Arc Length Calculator Inch Calculator Arc Length Vs Radius Arc length is a measurement of distance along the circumference of a circle or sector between. Finally, multiply that number by 2 × pi. Then, multiply that number by the radius of the circle. An arclength equal to one radius determines. Find the arc length of a sector by entering the central angle and radius in the calculator below. In. Arc Length Vs Radius.
From www.wikihow.com
How to Find Arc Length 10 Steps (with Pictures) wikiHow Arc Length Vs Radius Finally, multiply that number by 2 × pi. This is true for a circle of any size, as illustrated at right: An arclength equal to one radius determines. We see that an angle of one radian spans an arc whose length is the radius of the circle. Then the arc length \(s \) is: To find arc length, start by. Arc Length Vs Radius.
From www.physicsforums.com
Formula to find arc radius using arc length, chord length, and/or Arc Length Vs Radius Then the arc length \(s \) is: The length of an arc depends on the radius of a circle and the central angle θ. \[ s ~=~ r\,\theta \label{4.4} \] This is true for a circle of any size, as illustrated at right: We see that an angle of one radian spans an arc whose length is the radius of. Arc Length Vs Radius.
From www.youtube.com
Find Arc Length Given Radius and Angle in Radians Geometry YouTube Arc Length Vs Radius Finally, multiply that number by 2 × pi. This is true for a circle of any size, as illustrated at right: To find arc length, start by dividing the arc's central angle in degrees by 360. \[ s ~=~ r\,\theta \label{4.4} \] In a circle of radius \(r \), let \(s \) be the length of an arc intercepted by. Arc Length Vs Radius.
From www.youtube.com
How to Find the Arc Length Given the Radius and an Angle YouTube Arc Length Vs Radius Arc length is a measurement of distance along the circumference of a circle or sector between. \[ s ~=~ r\,\theta \label{4.4} \] To find arc length, start by dividing the arc's central angle in degrees by 360. This is true for a circle of any size, as illustrated at right: An arclength equal to one radius determines. Finally, multiply that. Arc Length Vs Radius.
From www.youtube.com
Radians as ratio of arc length to radius Circles High school Arc Length Vs Radius Arc length is a measurement of distance along the circumference of a circle or sector between. We see that an angle of one radian spans an arc whose length is the radius of the circle. Then the arc length \(s \) is: L = θ × r (when θ is in radians) l = θ × π 180 × r. Arc Length Vs Radius.
From www.wikihow.com
How to Find Arc Length Formulas and Examples Arc Length Vs Radius Then, multiply that number by the radius of the circle. Find the arc length of a sector by entering the central angle and radius in the calculator below. Finally, multiply that number by 2 × pi. L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) We. Arc Length Vs Radius.
From www.youtube.com
Day 13 HW (58 to 59) Find the Central Angle GIven the Arc Length and Arc Length Vs Radius Then the arc length \(s \) is: We see that an angle of one radian spans an arc whose length is the radius of the circle. L = θ × r (when θ is in radians) l = θ × π 180 × r (when θ is in degrees) Arc length is a measurement of distance along the circumference of. Arc Length Vs Radius.
From owlcation.com
How to Calculate Arc Length of a Circle, Segment and Sector Area Arc Length Vs Radius An arclength equal to one radius determines. \[ s ~=~ r\,\theta \label{4.4} \] To find arc length, start by dividing the arc's central angle in degrees by 360. This is true for a circle of any size, as illustrated at right: Finally, multiply that number by 2 × pi. We see that an angle of one radian spans an arc. Arc Length Vs Radius.