Asymptote Notes . An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: The following diagram shows the different types of asymptotes: Here are the rules to find asymptotes of a function y = f (x). An asymptote is a line that approaches closer to a given curve as one or both of x or. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Y coordinates tend to infinity but never intersects or crosses. Scroll down the page for more examples and solutions on how to find asymptotes. Asymptotes have a variety of applications: They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. The asymptote is indicated by the vertical dotted red line, and is referred to as a. In other words, asymptote is a line that a curve approaches as it moves towards infinity.
from amandapaffrath.weebly.com
Asymptotes have a variety of applications: In other words, asymptote is a line that a curve approaches as it moves towards infinity. They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. The asymptote is indicated by the vertical dotted red line, and is referred to as a. An asymptote is a line that approaches closer to a given curve as one or both of x or. Here are the rules to find asymptotes of a function y = f (x). An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: The following diagram shows the different types of asymptotes:
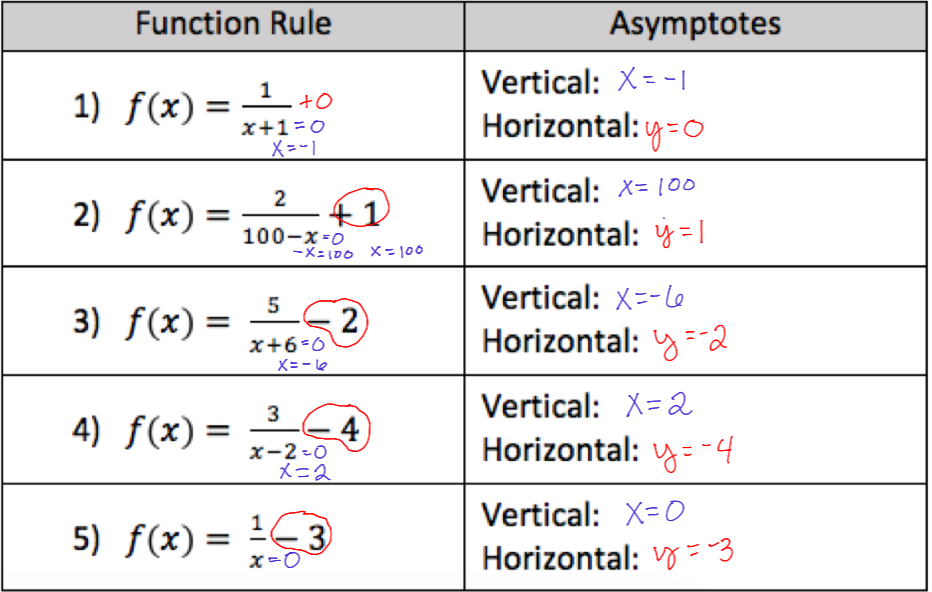
Rational Functions
Asymptote Notes An asymptote is a line that approaches closer to a given curve as one or both of x or. Here are the rules to find asymptotes of a function y = f (x). The following diagram shows the different types of asymptotes: Y coordinates tend to infinity but never intersects or crosses. An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Asymptotes have a variety of applications: An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. In other words, asymptote is a line that a curve approaches as it moves towards infinity. Scroll down the page for more examples and solutions on how to find asymptotes. An asymptote is a line that approaches closer to a given curve as one or both of x or. The asymptote is indicated by the vertical dotted red line, and is referred to as a.
From www.studocu.com
Asymptotes notes, 3 Asymptote Asymptotes, 3. Fall 2020 Note For Asymptote Notes The asymptote is indicated by the vertical dotted red line, and is referred to as a. They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. Here are the rules to find asymptotes of a function y = f (x). In other words, asymptote is a line that. Asymptote Notes.
From www.studocu.com
Limits Asymptotes Calculus Limits Asymptotes Calculus Notes Limits Asymptote Notes Y coordinates tend to infinity but never intersects or crosses. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Scroll down the page for more examples and solutions on how to find asymptotes. The following diagram shows the different types of asymptotes: Asymptotes have a variety of applications: An asymptote is a line that approaches closer to a given curve as one. Asymptote Notes.
From www.expii.com
Oblique Asymptotes of Rational Functions Expii Asymptote Notes The following diagram shows the different types of asymptotes: Here are the rules to find asymptotes of a function y = f (x). Scroll down the page for more examples and solutions on how to find asymptotes. Asymptotes have a variety of applications: An asymptote is a line that approaches closer to a given curve as one or both of. Asymptote Notes.
From www.studocu.com
Asymptote mth101 solution notes Asymptote An asymptote of a curve Asymptote Notes Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. The asymptote is indicated by the vertical dotted red line, and. Asymptote Notes.
From www.youtube.com
Curve Sketching with Asymptotes A Step by Step Example Using Calculus Asymptote Notes In other words, asymptote is a line that a curve approaches as it moves towards infinity. An asymptote is a line that approaches closer to a given curve as one or both of x or. The asymptote is indicated by the vertical dotted red line, and is referred to as a. Y coordinates tend to infinity but never intersects or. Asymptote Notes.
From www.youtube.com
asymptotes notes YouTube Asymptote Notes In other words, asymptote is a line that a curve approaches as it moves towards infinity. Y coordinates tend to infinity but never intersects or crosses. They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. Scroll down the page for more examples and solutions on how to. Asymptote Notes.
From www.studocu.com
Asymptotes notes January 24th finding verticle Asymptotes ° if him → Asymptote Notes Here are the rules to find asymptotes of a function y = f (x). In other words, asymptote is a line that a curve approaches as it moves towards infinity. Y coordinates tend to infinity but never intersects or crosses. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Asymptotes have a variety of applications: An asymptote is a line that approaches. Asymptote Notes.
From www.studocu.com
4) Vertical Asymptotes Vertical Asymptotes Definition If as (or Asymptote Notes Y coordinates tend to infinity but never intersects or crosses. The following diagram shows the different types of asymptotes: Scroll down the page for more examples and solutions on how to find asymptotes. The asymptote is indicated by the vertical dotted red line, and is referred to as a. In other words, asymptote is a line that a curve approaches. Asymptote Notes.
From www.cuemath.com
Vertical Asymptote Find, Rules, Definition, Graph Asymptote Notes An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: In other words, asymptote is a line that a curve approaches as it moves towards infinity. The following diagram shows the different types of asymptotes: Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. The asymptote is indicated by the vertical. Asymptote Notes.
From www.youtube.com
Section 2.6 Notes Slant Asymptotes YouTube Asymptote Notes In other words, asymptote is a line that a curve approaches as it moves towards infinity. Asymptotes have a variety of applications: An asymptote is a line that approaches closer to a given curve as one or both of x or. They are used in big o notation, they are simple approximations to complex equations, and they are useful for. Asymptote Notes.
From www.studypool.com
SOLUTION Asymptotes notes with practice questions Studypool Asymptote Notes An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Scroll down the page for more examples and solutions on how to find asymptotes. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Here are the rules to find asymptotes of a function y = f (x). An asymptote is a line. Asymptote Notes.
From www.slideserve.com
PPT Rational functions may have asymptotes (boundary lines). The f( x Asymptote Notes Y coordinates tend to infinity but never intersects or crosses. They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. The following diagram shows the different types of asymptotes: An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite. Asymptote Notes.
From testbook.com
Asymptotes Definition, Types, How to find, Method and Examples. Asymptote Notes An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: In other words, asymptote is a line that a curve approaches as it moves towards infinity. Here are the rules to find asymptotes of a function y = f (x). An asymptote is a straight line that constantly approaches. Asymptote Notes.
From www.youtube.com
asymptotes asymptotes notes pdf curve sketching curve tracing Asymptote Notes They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. Here are the rules to find asymptotes of a function y = f (x). An asymptote is a line that approaches closer to a given curve as one or both of x or. The asymptote is indicated by. Asymptote Notes.
From www.scribd.com
Asymptotes and Curve Tracing Notes PDF Asymptote Notes Asymptotes have a variety of applications: Scroll down the page for more examples and solutions on how to find asymptotes. The asymptote is indicated by the vertical dotted red line, and is referred to as a. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. The following diagram shows the different types of asymptotes: An asymptote is a line that approaches closer. Asymptote Notes.
From msalg22020.blogspot.com
Unit 4.6 Finding Horizontal Asymptotes Algebraically Asymptote Notes Asymptotes have a variety of applications: The following diagram shows the different types of asymptotes: An asymptote is a line that approaches closer to a given curve as one or both of x or. In other words, asymptote is a line that a curve approaches as it moves towards infinity. They are used in big o notation, they are simple. Asymptote Notes.
From www.pinterest.jp
Graphing Rational Functions, including Asymptotes She Loves Math Asymptote Notes Y coordinates tend to infinity but never intersects or crosses. Scroll down the page for more examples and solutions on how to find asymptotes. The following diagram shows the different types of asymptotes: An asymptote is a line that approaches closer to a given curve as one or both of x or. Asymptotes have a variety of applications: The asymptote. Asymptote Notes.
From annas-blog58.blogspot.com
Asymptote Of Tangent Intercepts and Asymptotes of Tangent Functions Asymptote Notes An asymptote is a line that approaches closer to a given curve as one or both of x or. Scroll down the page for more examples and solutions on how to find asymptotes. Y coordinates tend to infinity but never intersects or crosses. Asymptotes have a variety of applications: An asymptote is a straight line that constantly approaches a given. Asymptote Notes.
From www.slideserve.com
PPT Rational Functions and Asymptotes PowerPoint Presentation, free Asymptote Notes Y coordinates tend to infinity but never intersects or crosses. In other words, asymptote is a line that a curve approaches as it moves towards infinity. The asymptote is indicated by the vertical dotted red line, and is referred to as a. Here are the rules to find asymptotes of a function y = f (x). An asymptote is a. Asymptote Notes.
From amandapaffrath.weebly.com
Rational Functions Asymptote Notes The asymptote is indicated by the vertical dotted red line, and is referred to as a. An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Asymptotes have a variety of applications: Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Scroll down the page for more examples and solutions on how. Asymptote Notes.
From slidetodoc.com
Vertical and Horizontal Asymptotes of Rational Functions Rational Asymptote Notes Scroll down the page for more examples and solutions on how to find asymptotes. An asymptote is a line that approaches closer to a given curve as one or both of x or. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. The following diagram shows the different types of asymptotes: An asymptote is a straight line that constantly approaches a given. Asymptote Notes.
From www.slideserve.com
PPT Infinite Limits PowerPoint Presentation, free download ID2912470 Asymptote Notes Asymptotes have a variety of applications: An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. In other words, asymptote is a line that a curve approaches as it moves towards infinity. An asymptote is a line that approaches closer to a given. Asymptote Notes.
From moms-hub.blogspot.com
Moms Hub how to find slant asymptotes from a graph Asymptote Notes They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. Scroll down the page for more examples and solutions on how to find asymptotes. An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Horizontal asymptotes, vertical asymptotes,. Asymptote Notes.
From www.iitianacademy.com
AP Calculus AB and BC Chapter 1 Limits and Continuity 1.5 Limits Asymptote Notes The asymptote is indicated by the vertical dotted red line, and is referred to as a. In other words, asymptote is a line that a curve approaches as it moves towards infinity. The following diagram shows the different types of asymptotes: An asymptote is a line that approaches closer to a given curve as one or both of x or.. Asymptote Notes.
From mathodics.com
How to Find the Horizontal Asymptote With examples! Asymptote Notes An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: Y coordinates tend to infinity but never intersects or crosses. An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Here are the rules to find asymptotes of a. Asymptote Notes.
From www.youtube.com
Rational Functions Asymptotes, Domain and Range YouTube Asymptote Notes Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: An asymptote is a line that approaches closer to a given curve as one or both of x or. Scroll down the page for more examples and solutions on how to find. Asymptote Notes.
From neurologicablog.blogspot.com
Oblique Asymptote Khan / Calculus Asymptotes Solutions Examples Videos Asymptote Notes Asymptotes have a variety of applications: An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. The asymptote is indicated by the vertical dotted red line, and is referred to as a. They are used in big o notation, they are simple approximations to complex equations, and they are useful. Asymptote Notes.
From www.studypool.com
SOLUTION Asymptotes notes with practice questions Studypool Asymptote Notes In other words, asymptote is a line that a curve approaches as it moves towards infinity. The following diagram shows the different types of asymptotes: An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: An asymptote is a line that approaches closer to a given curve as one. Asymptote Notes.
From iteducationcourse.com
Horizontal Asymptotes Definition, Rules, Equation and more Asymptote Notes Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. Scroll down the page for more examples and solutions on how to find asymptotes. In other words, asymptote is a line that a curve approaches as it moves towards infinity. An asymptote is. Asymptote Notes.
From www.cuemath.com
Asymptotes Solved Examples Cuemath Asymptote Notes Here are the rules to find asymptotes of a function y = f (x). The asymptote is indicated by the vertical dotted red line, and is referred to as a. The following diagram shows the different types of asymptotes: An asymptote is a line that approaches closer to a given curve as one or both of x or. Scroll down. Asymptote Notes.
From www.scribd.com
Asymptotes Notes PDF Asymptote Notes Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Asymptotes have a variety of applications: The following diagram shows the different types of asymptotes: The asymptote is indicated by the vertical dotted red line, and is referred to as a. In other words, asymptote is a line that a curve approaches as it moves towards infinity. Scroll down the page for more. Asymptote Notes.
From www.cuemath.com
Asymptotes Solved Examples Cuemath Asymptote Notes Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. An asymptote is a line or a curve that the graph of a function approaches, as shown in the figure below: They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. The asymptote is indicated by the vertical dotted red line,. Asymptote Notes.
From www.studocu.com
Section 1 1.3 lecture notes Horizontal Asymptotes What does the Asymptote Notes An asymptote is a line that approaches closer to a given curve as one or both of x or. They are used in big o notation, they are simple approximations to complex equations, and they are useful for graphing rational equations. In other words, asymptote is a line that a curve approaches as it moves towards infinity. The following diagram. Asymptote Notes.
From www.houseofmath.com
How to Interpret and Calculate Asymptotes of a Function Asymptote Notes The asymptote is indicated by the vertical dotted red line, and is referred to as a. Horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Here are the rules to find asymptotes of a function y = f (x). An asymptote is a straight line that constantly approaches a given curve but does not meet at any infinite distance. In other words,. Asymptote Notes.
From slideplayer.com
Asymptotes Horizontal Asymptotes Vertical Asymptotes ppt download Asymptote Notes Here are the rules to find asymptotes of a function y = f (x). In other words, asymptote is a line that a curve approaches as it moves towards infinity. An asymptote is a line that approaches closer to a given curve as one or both of x or. An asymptote is a straight line that constantly approaches a given. Asymptote Notes.