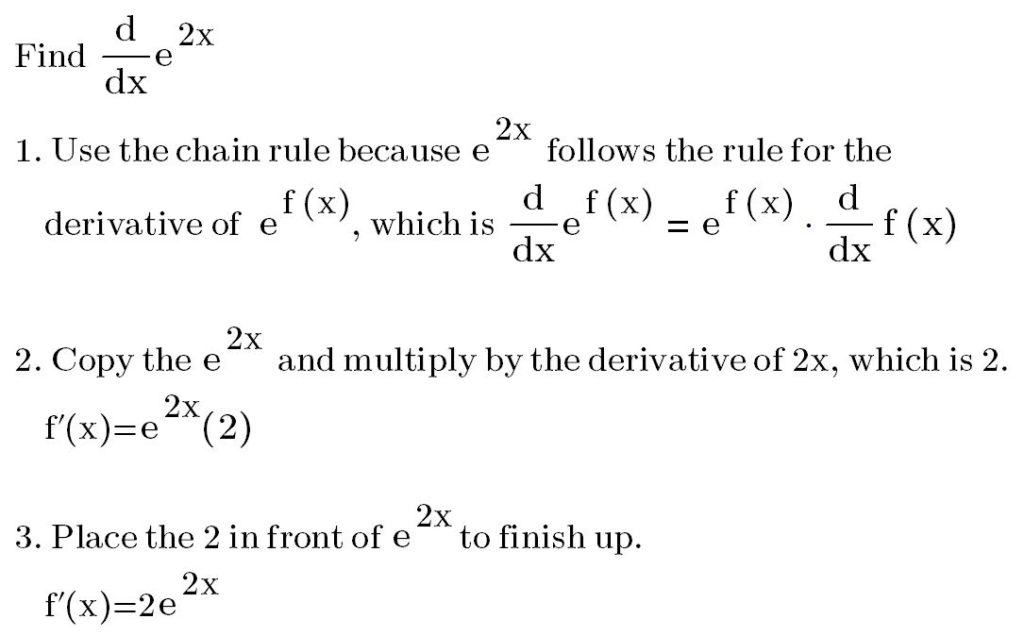Derivatives And Integrals Of E . The derivative of the exponential function e x is equal to e. derivatives and integrals of exponential functions. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. 2x = (eln2)x = exln2. the derivative and integral of the exponential function. Definitions and properties of the exponential function. We will use the derivative of the inverse theorem to find the derivative of. the exponential function, y= ex, y = e x, is its own derivative and its own integral. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. we first convert into base e e as follows: Now that we have the derivative of the natural exponential function, we can use implicit. The function y=e x is called the exponential function. the exponential function is perhaps the most efficient function in terms of the operations of calculus. derivative of the logarithmic function. the derivative of the exponential.
from calculuscoaches.com
the exponential function is perhaps the most efficient function in terms of the operations of calculus. the derivative of the exponential. We will use the derivative of the inverse theorem to find the derivative of. we first convert into base e e as follows: The function y=e x is called the exponential function. derivative of the logarithmic function. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. derivatives and integrals of exponential functions. the derivative and integral of the exponential function. Now that we have the derivative of the natural exponential function, we can use implicit.
Unlock step by step directions for finding the derivative of e^(2x) Calculus Coaches
Derivatives And Integrals Of E the derivative of the exponential. The function y=e x is called the exponential function. the exponential function is perhaps the most efficient function in terms of the operations of calculus. derivative of the logarithmic function. Definitions and properties of the exponential function. the derivative and integral of the exponential function. we first convert into base e e as follows: the exponential function, y= ex, y = e x, is its own derivative and its own integral. 2x = (eln2)x = exln2. the derivative of the exponential. The derivative of the exponential function e x is equal to e. derivatives and integrals of exponential functions. Now that we have the derivative of the natural exponential function, we can use implicit. We will use the derivative of the inverse theorem to find the derivative of. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the.
From dxocwgfkz.blob.core.windows.net
Engineering Calculus And Differential Equations at Mark Badgett blog Derivatives And Integrals Of E Now that we have the derivative of the natural exponential function, we can use implicit. We will use the derivative of the inverse theorem to find the derivative of. the derivative of the exponential. Definitions and properties of the exponential function. the derivative and integral of the exponential function. The derivative of the exponential function e x is. Derivatives And Integrals Of E.
From calcworkshop.com
Derivative of Exponential Function (Fully Explained!) Derivatives And Integrals Of E the derivative of the exponential. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. We will use the derivative of the inverse theorem to find the derivative of. the exponential function, y= ex, y = e x, is its own derivative and its own integral. . Derivatives And Integrals Of E.
From www.youtube.com
Derivative and Integral of ln and e YouTube Derivatives And Integrals Of E 2x = (eln2)x = exln2. The derivative of the exponential function e x is equal to e. the exponential function, y= ex, y = e x, is its own derivative and its own integral. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. Now that we have the derivative. Derivatives And Integrals Of E.
From mungfali.com
Tablas De Formulas Derivatives And Integrals Of E derivative of the logarithmic function. Now that we have the derivative of the natural exponential function, we can use implicit. the exponential function, y= ex, y = e x, is its own derivative and its own integral. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the.. Derivatives And Integrals Of E.
From www.studypool.com
SOLUTION Common derivatives integrals Studypool Derivatives And Integrals Of E derivative of the logarithmic function. The derivative of the exponential function e x is equal to e. Definitions and properties of the exponential function. The function y=e x is called the exponential function. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. the exponential function is. Derivatives And Integrals Of E.
From bitdrivencircuits.com
Table of Derivatives Derivatives And Integrals Of E derivatives and integrals of exponential functions. the exponential function, y= ex, y = e x, is its own derivative and its own integral. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. 2x = (eln2)x = exln2. Now that we have the derivative of the natural exponential function,. Derivatives And Integrals Of E.
From www.youtube.com
Why is the derivative of the Integral is the function itselfWhat is the derivative of the Derivatives And Integrals Of E the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. derivative of the logarithmic function. the derivative and integral of the exponential function. The function y=e x is called the exponential function. We will use the derivative of the inverse theorem to find the derivative of. . Derivatives And Integrals Of E.
From en.neurochispas.com
Derivatives and Integrals of Exponential Functions Neurochispas Derivatives And Integrals Of E 2x = (eln2)x = exln2. Definitions and properties of the exponential function. derivatives and integrals of exponential functions. the derivative and integral of the exponential function. Now that we have the derivative of the natural exponential function, we can use implicit. we first convert into base e e as follows: derivative of the logarithmic function. The. Derivatives And Integrals Of E.
From ar.inspiredpencil.com
Integral Rules E Derivatives And Integrals Of E the exponential function is perhaps the most efficient function in terms of the operations of calculus. 2x = (eln2)x = exln2. the exponential function, y= ex, y = e x, is its own derivative and its own integral. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. . Derivatives And Integrals Of E.
From calculuscoaches.com
Unlock step by step directions for finding the derivative of e^(2x) Calculus Coaches Derivatives And Integrals Of E The function y=e x is called the exponential function. 2x = (eln2)x = exln2. we first convert into base e e as follows: The derivative of the exponential function e x is equal to e. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. the number e is. Derivatives And Integrals Of E.
From www.showme.com
Derivative of e raised to a function Math ShowMe Derivatives And Integrals Of E the derivative of the exponential. We will use the derivative of the inverse theorem to find the derivative of. 2x = (eln2)x = exln2. Definitions and properties of the exponential function. The function y=e x is called the exponential function. The derivative of the exponential function e x is equal to e. Now that we have the derivative of. Derivatives And Integrals Of E.
From images.modishstore.com
Tabela Derivadas E Integrais MODISEDU Derivatives And Integrals Of E we first convert into base e e as follows: derivative of the logarithmic function. the derivative and integral of the exponential function. Now that we have the derivative of the natural exponential function, we can use implicit. We will use the derivative of the inverse theorem to find the derivative of. the number e is often. Derivatives And Integrals Of E.
From nghs12acc.blogspot.com
core pure 3 notes integrals involving exponentials Derivatives And Integrals Of E The derivative of the exponential function e x is equal to e. Definitions and properties of the exponential function. derivative of the logarithmic function. the exponential function, y= ex, y = e x, is its own derivative and its own integral. we first convert into base e e as follows: Now that we have the derivative of. Derivatives And Integrals Of E.
From www.slideserve.com
PPT 5.4 Exponential Functions Differentiation and Integration PowerPoint Presentation ID Derivatives And Integrals Of E we first convert into base e e as follows: the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. the derivative of the exponential. the derivative and integral of the exponential function. derivative of the logarithmic function. Now that we have the derivative of the. Derivatives And Integrals Of E.
From studylib.net
Common Derivatives and Integrals Derivatives And Integrals Of E Now that we have the derivative of the natural exponential function, we can use implicit. we first convert into base e e as follows: 2x = (eln2)x = exln2. We will use the derivative of the inverse theorem to find the derivative of. the derivative of the exponential. The function y=e x is called the exponential function. . Derivatives And Integrals Of E.
From www.slideserve.com
PPT Calculus II Chapter 6 Section 7 Derivatives & Integrals of exponential and log functions Derivatives And Integrals Of E we first convert into base e e as follows: the exponential function is perhaps the most efficient function in terms of the operations of calculus. The function y=e x is called the exponential function. derivative of the logarithmic function. The derivative of the exponential function e x is equal to e. the derivative of the exponential.. Derivatives And Integrals Of E.
From www.scribd.com
Mathematics Derivatives and Integrals Chart Derivatives And Integrals Of E Definitions and properties of the exponential function. Now that we have the derivative of the natural exponential function, we can use implicit. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections. Derivatives And Integrals Of E.
From math.stackexchange.com
Getting the derivative of a function in an integral form Mathematics Stack Exchange Derivatives And Integrals Of E the exponential function, y= ex, y = e x, is its own derivative and its own integral. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. Definitions and properties of the exponential function. the derivative of the exponential. derivative of the logarithmic function. the. Derivatives And Integrals Of E.
From www.slideserve.com
PPT 5.4 Exponential Functions Differentiation and Integration PowerPoint Presentation ID Derivatives And Integrals Of E Now that we have the derivative of the natural exponential function, we can use implicit. the exponential function is perhaps the most efficient function in terms of the operations of calculus. The derivative of the exponential function e x is equal to e. the exponential function, y= ex, y = e x, is its own derivative and its. Derivatives And Integrals Of E.
From hyperphysics.phy-astr.gsu.edu
Definite Integrals Derivatives And Integrals Of E the derivative of the exponential. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. Now that we have the derivative of the natural exponential function, we can use implicit. derivatives and integrals of exponential functions. the number e is often associated with compounded or accelerating growth, as. Derivatives And Integrals Of E.
From www.cuemath.com
Integration Properties, Examples, Formula, Methods Derivatives And Integrals Of E the exponential function is perhaps the most efficient function in terms of the operations of calculus. 2x = (eln2)x = exln2. derivatives and integrals of exponential functions. Now that we have the derivative of the natural exponential function, we can use implicit. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x. Derivatives And Integrals Of E.
From www.studypool.com
SOLUTION Formulas and concept in integral calculus Studypool Derivatives And Integrals Of E The derivative of the exponential function e x is equal to e. We will use the derivative of the inverse theorem to find the derivative of. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. the derivative and integral of the exponential function. derivative of the logarithmic function.. Derivatives And Integrals Of E.
From www.studypool.com
SOLUTION Integration and differentiation formula sheet Studypool Derivatives And Integrals Of E Definitions and properties of the exponential function. the exponential function is perhaps the most efficient function in terms of the operations of calculus. The function y=e x is called the exponential function. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. We will use the derivative of. Derivatives And Integrals Of E.
From bitdrivencircuits.com
Table of Derivatives Derivatives And Integrals Of E the exponential function is perhaps the most efficient function in terms of the operations of calculus. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. derivatives and integrals of exponential functions. The derivative of the exponential function e x is equal to e. the exponential function, y=. Derivatives And Integrals Of E.
From www.vrogue.co
Pdf Derivative Table Integral And Its Rules Tabela De vrogue.co Derivatives And Integrals Of E derivative of the logarithmic function. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. 2x = (eln2)x = exln2. Now that we have the derivative of the natural exponential function, we can use implicit. The derivative of the exponential function e x is equal to e. the derivative. Derivatives And Integrals Of E.
From calculuscoaches.com
finding the derivative of e^(x) Calculus Coaches Derivatives And Integrals Of E 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. 2x = (eln2)x = exln2. The function y=e x is called the exponential function. Definitions and properties of the exponential function. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about. Derivatives And Integrals Of E.
From mavink.com
Printable Table Of Integrals Derivatives And Integrals Of E the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. we first convert into base e e as follows: the derivative and integral of the exponential function. Now that we have the derivative of the natural exponential function, we can use implicit. The derivative of the exponential. Derivatives And Integrals Of E.
From www.youtube.com
Derivatives and Integrals of Expressions with e part 4 YouTube Derivatives And Integrals Of E 2x = (eln2)x = exln2. the derivative of the exponential. Definitions and properties of the exponential function. We will use the derivative of the inverse theorem to find the derivative of. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. derivatives and integrals of exponential functions. the. Derivatives And Integrals Of E.
From quizizz.com
50+ derivatives of integral functions worksheets for 11th Class on Quizizz Free & Printable Derivatives And Integrals Of E the exponential function is perhaps the most efficient function in terms of the operations of calculus. derivative of the logarithmic function. 2x = (eln2)x = exln2. Now that we have the derivative of the natural exponential function, we can use implicit. we first convert into base e e as follows: The function y=e x is called the. Derivatives And Integrals Of E.
From www.theacetutors.com
Derivative Rules Cheat Sheet Calculus Ace Tutors Blog Derivatives And Integrals Of E We will use the derivative of the inverse theorem to find the derivative of. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. 2x = (eln2)x = exln2. Definitions and properties of the exponential function. the exponential function is perhaps the most efficient function in terms of. Derivatives And Integrals Of E.
From www.deviantart.com
Derivative and Integral Formula Wallpaper 2 by SawyerTHEBEST on DeviantArt Derivatives And Integrals Of E the derivative of the exponential. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. the exponential function, y= ex, y = e x, is its own derivative and its own integral. derivative of the logarithmic function. 2^x = \left ( e^ { \ln 2 }. Derivatives And Integrals Of E.
From www.chegg.com
Solved Determine which of the integrals can be found using Derivatives And Integrals Of E Now that we have the derivative of the natural exponential function, we can use implicit. 2x = (eln2)x = exln2. 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. The derivative of the exponential function e x is equal to e. the number e is often associated with compounded. Derivatives And Integrals Of E.
From giasutamtaiduc.com
Differentiation and Integration Formula ⭐️⭐️⭐️⭐️⭐ Derivatives And Integrals Of E the exponential function, y= ex, y = e x, is its own derivative and its own integral. derivatives and integrals of exponential functions. the number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the. Definitions and properties of the exponential function. 2x = (eln2)x = exln2. we. Derivatives And Integrals Of E.
From www.pinterest.com
derivative and integral table Math, Derivative, Physics Derivatives And Integrals Of E the exponential function is perhaps the most efficient function in terms of the operations of calculus. We will use the derivative of the inverse theorem to find the derivative of. 2x = (eln2)x = exln2. Definitions and properties of the exponential function. we first convert into base e e as follows: Now that we have the derivative of. Derivatives And Integrals Of E.
From studylib.net
Common Derivatives Integrals Derivatives And Integrals Of E 2^x = \left ( e^ { \ln 2 } \right) ^ x = e^ { x \ln 2 }. Definitions and properties of the exponential function. derivatives and integrals of exponential functions. Now that we have the derivative of the natural exponential function, we can use implicit. the derivative and integral of the exponential function. the exponential. Derivatives And Integrals Of E.