Equilateral Triangle Inscribed In A Circle Find Area . Find the perimeter of the triangle. [use π = 22 7. The side of the equilateral triangle is r = side / √3. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The area of a circle inscribed in an equilateral triangle is 154 cm2. An equilateral triangle has side length x. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. Find the circle's area in terms of x. ⇒ side = r × √3.
from atlanticgmat.com
⇒ side = r × √3. An equilateral triangle has side length x. Find the circle's area in terms of x. Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle. [use π = 22 7. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius?
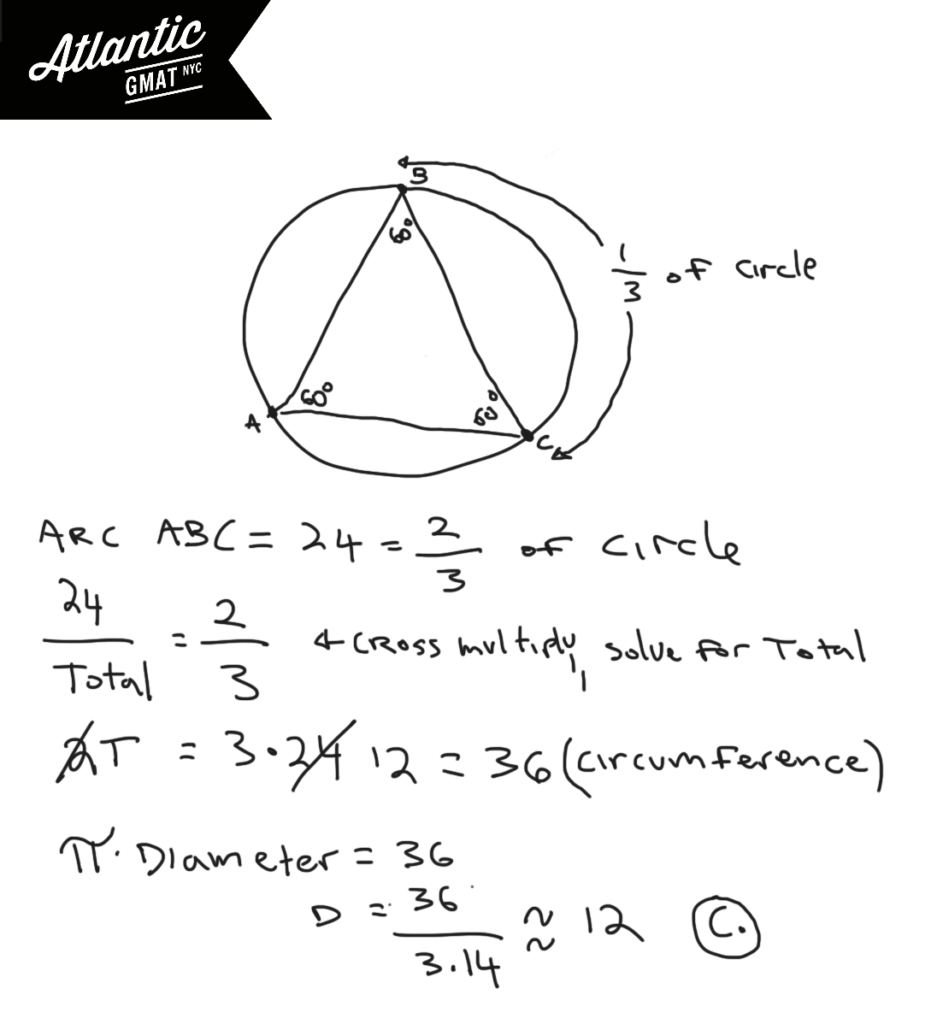
In the figure above, equilateral triangle ABC is inscribed in the
Equilateral Triangle Inscribed In A Circle Find Area If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? [use π = 22 7. The area of a circle inscribed in an equilateral triangle is 154 cm2. ⇒ side = r × √3. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. Find the circle's area in terms of x. Find the perimeter of the triangle. Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. An equilateral triangle has side length x. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. The side of the equilateral triangle is r = side / √3. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle.
From www.vrogue.co
Formulas Radius Of Inscribed And Circumscribed Circle vrogue.co Equilateral Triangle Inscribed In A Circle Find Area An equilateral triangle has side length x. ⇒ side = r × √3. Find the perimeter of the triangle. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr. Equilateral Triangle Inscribed In A Circle Find Area.
From www.youtube.com
An equilateral triangle of side 9cm inscribed in a circle The radius of Equilateral Triangle Inscribed In A Circle Find Area The side of the equilateral triangle is r = side / √3. [use π = 22 7. Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. The area of a circle inscribed in an equilateral triangle is 154 cm2. To find the area of an equilateral triangle inscribed. Equilateral Triangle Inscribed In A Circle Find Area.
From ar.inspiredpencil.com
Inscribed Triangle Equilateral Triangle Inscribed In A Circle Find Area Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. The side of the equilateral triangle is r = side / √3. ⇒ side = r × √3. Find the perimeter of the triangle. Find the circle's area in terms of x. If there is an equilateral triangle in. Equilateral Triangle Inscribed In A Circle Find Area.
From www.tutorix.com
A circle is inscribed in an equilateral triangle A Tutorix Equilateral Triangle Inscribed In A Circle Find Area The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. ⇒ side = r × √3. An equilateral triangle has side length x. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. Find the circle's area in terms. Equilateral Triangle Inscribed In A Circle Find Area.
From www.doubtnut.com
In Fig. an equilateral triangle A B C of side 6 cm has been inscribed Equilateral Triangle Inscribed In A Circle Find Area To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The area of a circle inscribed in an equilateral triangle is 154 cm2. [use π = 22 7. Find the circle's area in terms of x. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0. Equilateral Triangle Inscribed In A Circle Find Area.
From frojeostern.com
Show that the isosceles triangle of maximum area inscribed in a given Equilateral Triangle Inscribed In A Circle Find Area The area of a circle inscribed in an equilateral triangle is 154 cm2. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. The side of the equilateral triangle is r = side / √3. Find the perimeter of the triangle. If there is an equilateral. Equilateral Triangle Inscribed In A Circle Find Area.
From byjus.com
1. If PQR is an equilateral Triangle inscribed in a circle and A be any Equilateral Triangle Inscribed In A Circle Find Area An equilateral triangle has side length x. The side of the equilateral triangle is r = side / √3. [use π = 22 7. ⇒ side = r × √3. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Find the perimeter of the triangle. The area. Equilateral Triangle Inscribed In A Circle Find Area.
From byjus.com
if an equilateral triangle is inscribed in a circle of radius 10 cm Equilateral Triangle Inscribed In A Circle Find Area To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the circle's area in terms of x. ⇒ side = r × √3. The side of the equilateral triangle is r. Equilateral Triangle Inscribed In A Circle Find Area.
From www.youtube.com
Area of the shaded part An Equilateral Triangle Inscribed in a Circle Equilateral Triangle Inscribed In A Circle Find Area To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. Let abc equatorial triangle inscribed in the circle with radius r. Equilateral Triangle Inscribed In A Circle Find Area.
From www.youtube.com
special triangles inscribed area of shaded region equilateral circle Equilateral Triangle Inscribed In A Circle Find Area E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. Find the perimeter of the triangle. The area of a circle inscribed in an equilateral triangle is 154 cm2. An equilateral triangle has side length x. The side of the equilateral triangle is r = side / √3. Find the circle's area in. Equilateral Triangle Inscribed In A Circle Find Area.
From mungfali.com
Equilateral Triangle In A Circle Equilateral Triangle Inscribed In A Circle Find Area E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. Find the perimeter of the triangle. The area of a circle inscribed in an equilateral triangle is 154 cm2. The side of the equilateral triangle is r = side / √3. Find the circle's area in terms of x. To find the area. Equilateral Triangle Inscribed In A Circle Find Area.
From www.teachoo.com
Show that triangle of maximum area that can be inscribed in a circle Equilateral Triangle Inscribed In A Circle Find Area If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Find the perimeter of the triangle. The side of the equilateral triangle is r = side / √3. Find the circle's area in terms of x. To find the area of an equilateral triangle inscribed in a circle,. Equilateral Triangle Inscribed In A Circle Find Area.
From www.geeksforgeeks.org
Area of Equilateral triangle inscribed in a Circle of radius R Equilateral Triangle Inscribed In A Circle Find Area Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. Find the circle's area in terms of x. ⇒ side = r × √3. An equilateral triangle has side length x. The area of a circle inscribed in an equilateral triangle is 154 cm2. The side of the equilateral. Equilateral Triangle Inscribed In A Circle Find Area.
From www.vrogue.co
An Equilateral Triangle Abc Is Inscribed In A Circle vrogue.co Equilateral Triangle Inscribed In A Circle Find Area [use π = 22 7. The side of the equilateral triangle is r = side / √3. The area of a circle inscribed in an equilateral triangle is 154 cm2. An equilateral triangle has side length x. Find the perimeter of the triangle. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would.. Equilateral Triangle Inscribed In A Circle Find Area.
From www.vrogue.co
Solved If A Triangle Is Inscribed In A Circle So That vrogue.co Equilateral Triangle Inscribed In A Circle Find Area Find the perimeter of the triangle. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The side of the equilateral triangle is r = side / √3. If there is an equilateral triangle in a circle, would the midpoint of any of the 3. Equilateral Triangle Inscribed In A Circle Find Area.
From brainly.in
in fig a circle is inscribed in an equilateral triangle abc of side Equilateral Triangle Inscribed In A Circle Find Area Find the circle's area in terms of x. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? To find the area of an equilateral triangle inscribed in a circle, we. Equilateral Triangle Inscribed In A Circle Find Area.
From byjus.com
An equilateral triangle ABC is inscribed in a circle with centre O Equilateral Triangle Inscribed In A Circle Find Area ⇒ side = r × √3. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the circle's area in terms of x. To find the area of an equilateral triangle inscribed. Equilateral Triangle Inscribed In A Circle Find Area.
From edurev.in
THE AREA OF A CIRCLE INSCRIBED IN AN EQUILATERAL TRIANGLE IS 154 CM SQ Equilateral Triangle Inscribed In A Circle Find Area To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. Find the circle's area in terms of x. Find the perimeter of the triangle.. Equilateral Triangle Inscribed In A Circle Find Area.
From www.toppr.com
An equilateral triangle of side 9 cm is inscribed in a circle. Find the Equilateral Triangle Inscribed In A Circle Find Area Find the circle's area in terms of x. Find the perimeter of the triangle. An equilateral triangle has side length x. The area of a circle inscribed in an equilateral triangle is 154 cm2. ⇒ side = r × √3. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half. Equilateral Triangle Inscribed In A Circle Find Area.
From byjus.com
An equilateral triangle of side 9 cm is inscribed in a circle then the Equilateral Triangle Inscribed In A Circle Find Area To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? ⇒ side = r × √3. [use π = 22 7. Let abc. Equilateral Triangle Inscribed In A Circle Find Area.
From mathibayon.blogspot.com
Formulas Radius of Inscribed and Circumscribed Circle in a Triangle Equilateral Triangle Inscribed In A Circle Find Area To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? Find the perimeter of the triangle. E.g if the radius was 6 and. Equilateral Triangle Inscribed In A Circle Find Area.
From socratic.org
A triangle has corners at (4 , 5 ), (3 ,2 ), and (1 ,3 ). What is the Equilateral Triangle Inscribed In A Circle Find Area E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of. Equilateral Triangle Inscribed In A Circle Find Area.
From byjus.com
An equilateral triangle ABC is inscribed in a circle of radius 12 cm Equilateral Triangle Inscribed In A Circle Find Area ⇒ side = r × √3. An equilateral triangle has side length x. Find the circle's area in terms of x. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. Find the perimeter of the triangle. The side of the equilateral triangle is r. Equilateral Triangle Inscribed In A Circle Find Area.
From www.doubtnut.com
ABC is an equilateral triangle inscribed in a circle of radius 4 cm. F Equilateral Triangle Inscribed In A Circle Find Area An equilateral triangle has side length x. Find the circle's area in terms of x. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle. Equilateral Triangle Inscribed In A Circle Find Area.
From byjus.com
35. Find the side of an equilateral triangle inscribed in a circle of Equilateral Triangle Inscribed In A Circle Find Area The area of a circle inscribed in an equilateral triangle is 154 cm2. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in. Equilateral Triangle Inscribed In A Circle Find Area.
From atlanticgmat.com
In the figure above, equilateral triangle ABC is inscribed in the Equilateral Triangle Inscribed In A Circle Find Area ⇒ side = r × √3. The side of the equilateral triangle is r = side / √3. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius? The area of a circle inscribed in an equilateral triangle is 154 cm2. E.g if the radius was 6 and. Equilateral Triangle Inscribed In A Circle Find Area.
From brainly.in
The radius of a circle inscribed in an equilateral triangle is 10 cm Equilateral Triangle Inscribed In A Circle Find Area The area of a circle inscribed in an equilateral triangle is 154 cm2. Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. The side of the equilateral triangle is r = side / √3. [use π = 22 7. To find the area of an equilateral triangle inscribed. Equilateral Triangle Inscribed In A Circle Find Area.
From ar.inspiredpencil.com
Circumscribed Equilateral Triangle Equilateral Triangle Inscribed In A Circle Find Area E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. The area of a circle inscribed in an equilateral triangle is 154 cm2. To find the area of an equilateral triangle inscribed. Equilateral Triangle Inscribed In A Circle Find Area.
From brainly.in
the area of a circle inscribed in an equilateral triangle is 154 cm Equilateral Triangle Inscribed In A Circle Find Area The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an equilateral triangle inscribed in the circle. Find the perimeter of the triangle. Find the circle's area in terms of x. If there is an equilateral triangle in a circle, would the midpoint of any of the 3 sides be half the radius?. Equilateral Triangle Inscribed In A Circle Find Area.
From www.meritnation.com
ABC is an equilateral triangle inscribed in a circle of radius 4cm find Equilateral Triangle Inscribed In A Circle Find Area Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. The area of a circle inscribed in an equilateral triangle is 154 cm2. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0. Equilateral Triangle Inscribed In A Circle Find Area.
From www.meritnation.com
In the given figure,PQR is an equilateral triangle inscribed in a Equilateral Triangle Inscribed In A Circle Find Area ⇒ side = r × √3. [use π = 22 7. The area of a circle inscribed in an equilateral triangle is 154 cm2. The side of the equilateral triangle is r = side / √3. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral. Equilateral Triangle Inscribed In A Circle Find Area.
From lessonschoolworkday.z14.web.core.windows.net
The Area Of A Equilateral Triangle Equilateral Triangle Inscribed In A Circle Find Area Find the circle's area in terms of x. The side of the equilateral triangle is r = side / √3. [use π = 22 7. Let abc equatorial triangle inscribed in the circle with radius r applying law of sine to the triangle obc, we get. Find the perimeter of the triangle. ⇒ side = r × √3. The area. Equilateral Triangle Inscribed In A Circle Find Area.
From www.youtube.com
Radius of the incircle of an Equilateral Triangle YouTube Equilateral Triangle Inscribed In A Circle Find Area The side of the equilateral triangle is r = side / √3. [use π = 22 7. The area of a circle inscribed in an equilateral triangle is 154 cm2. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. E.g if the radius was. Equilateral Triangle Inscribed In A Circle Find Area.
From www.teachoo.com
Show that triangle of maximum area that can be inscribed in a circle Equilateral Triangle Inscribed In A Circle Find Area Find the perimeter of the triangle. E.g if the radius was 6 and at the midpoint of the triangle (call it b) would. An equilateral triangle has side length x. The side of the equilateral triangle is r = side / √3. The correct option is b3√34(g2+f2−c) given circle is x2+y2+2gx+2fy+c=0 let c be its centre and pqr be an. Equilateral Triangle Inscribed In A Circle Find Area.
From byjus.com
In the given figure, a circle is inscribed in an equilateral triangle Equilateral Triangle Inscribed In A Circle Find Area An equilateral triangle has side length x. To find the area of an equilateral triangle inscribed in a circle, we have to find the length of the side of the equilateral triangle. ⇒ side = r × √3. The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle. The correct option. Equilateral Triangle Inscribed In A Circle Find Area.