Combinations Permutations And Factorials . The formulas for each are very similar, there is. We have n choices each. Using the concept of factorials, many complicated things. Let’s denote this quantity as \(p_k^n\). if the order of the items is important, use a permutation. If the order of the items is not important, use a. the combination formula the number of combinations of n things taken r at a time:! we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. These are the easiest to calculate. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? When a thing has n different types. In considering the number of. one of the most basic concepts of permutations and combinations is the use of factorial notation.
from www.studypug.com
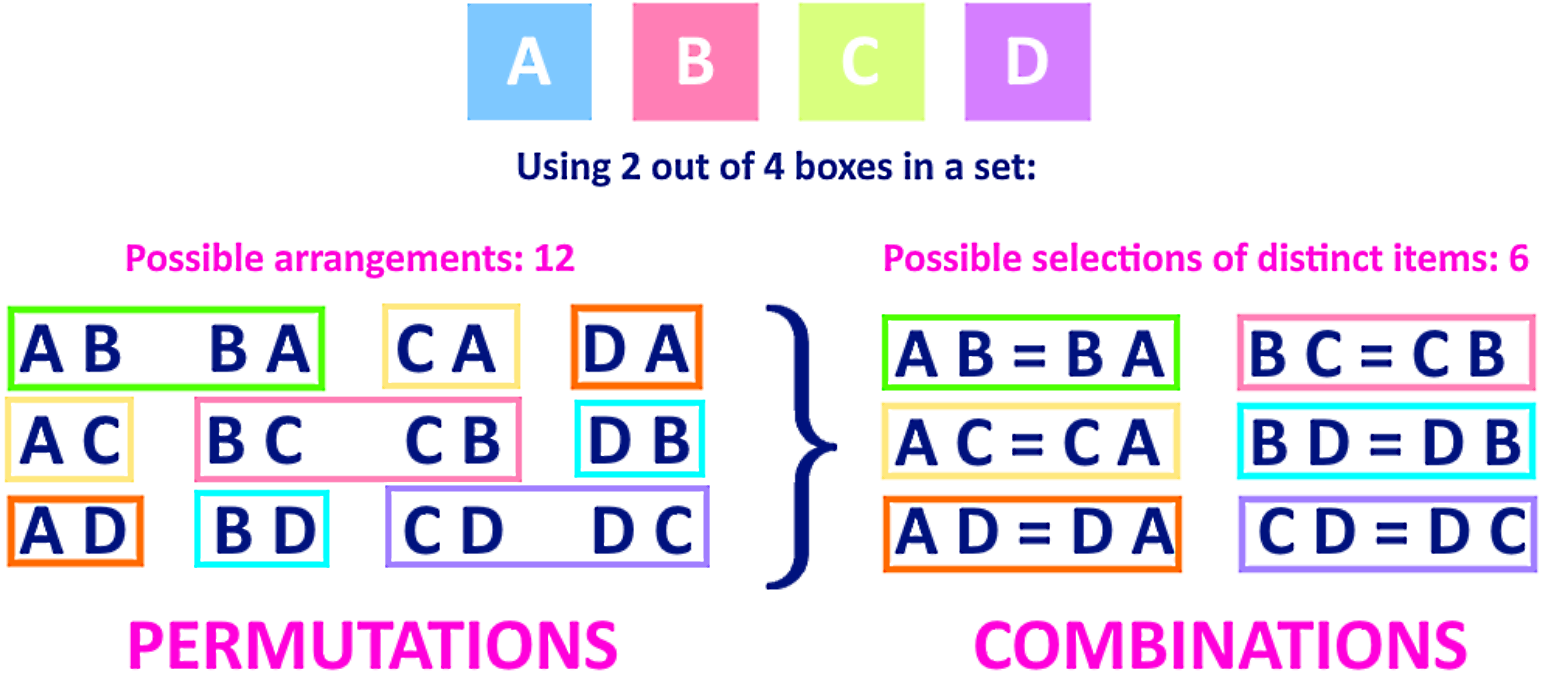
we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. We have n choices each. These are the easiest to calculate. one of the most basic concepts of permutations and combinations is the use of factorial notation. The formulas for each are very similar, there is. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? Let’s denote this quantity as \(p_k^n\). If the order of the items is not important, use a. In considering the number of. the combination formula the number of combinations of n things taken r at a time:!
Understanding permutations vs. combinations StudyPug
Combinations Permutations And Factorials if the order of the items is important, use a permutation. Using the concept of factorials, many complicated things. Let’s denote this quantity as \(p_k^n\). When a thing has n different types. The formulas for each are very similar, there is. These are the easiest to calculate. If the order of the items is not important, use a. We have n choices each. one of the most basic concepts of permutations and combinations is the use of factorial notation. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. the combination formula the number of combinations of n things taken r at a time:! In considering the number of. if the order of the items is important, use a permutation.
From www.cuemath.com
Permutation and Combination Definition, Formulas, Derivation, Examples Combinations Permutations And Factorials These are the easiest to calculate. one of the most basic concepts of permutations and combinations is the use of factorial notation. Using the concept of factorials, many complicated things. if the order of the items is important, use a permutation. If the order of the items is not important, use a. The formulas for each are very. Combinations Permutations And Factorials.
From slidetodoc.com
Lesson 42 Permutations and combinations factorial A factorial Combinations Permutations And Factorials in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? The formulas for each are very similar, there is. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. the combination formula the number of combinations of n things taken r at a time:! Using the concept. Combinations Permutations And Factorials.
From slidetodoc.com
10 8 Combinations 10 8 Combinationsand and Permutations Combinations Permutations And Factorials In considering the number of. if the order of the items is important, use a permutation. If the order of the items is not important, use a. We have n choices each. one of the most basic concepts of permutations and combinations is the use of factorial notation. When a thing has n different types. the combination. Combinations Permutations And Factorials.
From www.slideshare.net
Factorials permutations Combinations Permutations And Factorials the combination formula the number of combinations of n things taken r at a time:! we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. one of the most basic concepts of permutations and combinations is the use of factorial notation. When a thing has n different types. Using the concept of factorials, many complicated things.. Combinations Permutations And Factorials.
From dxowmpakr.blob.core.windows.net
Factorials Permutations And Combinations Formula at Vanessa Cabral blog Combinations Permutations And Factorials the combination formula the number of combinations of n things taken r at a time:! Let’s denote this quantity as \(p_k^n\). in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? When a thing has n different types. If the order of the items is not important, use a.. Combinations Permutations And Factorials.
From www.youtube.com
Permutations, Combinations, and Factorials (ACT Math Review Video Course 29 of 65) YouTube Combinations Permutations And Factorials in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? one of the most basic concepts of permutations and combinations is the use of factorial notation. the combination formula the number of combinations of n things taken r at a time:! If the order of the items is. Combinations Permutations And Factorials.
From slidetodoc.com
Lesson 42 Permutations and combinations factorial A factorial Combinations Permutations And Factorials we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. if the order of the items is important, use a permutation. When a thing has n different types. Using the concept of factorials, many complicated things. Let’s denote this quantity as \(p_k^n\). the combination formula the number of combinations of n things taken r at a. Combinations Permutations And Factorials.
From dxowmpakr.blob.core.windows.net
Factorials Permutations And Combinations Formula at Vanessa Cabral blog Combinations Permutations And Factorials we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. When a thing has n different types. one of the most basic concepts of permutations and combinations is the use of factorial notation. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? The formulas for each. Combinations Permutations And Factorials.
From www.slideserve.com
PPT Part 1 Module 5 Factorials, Permutations, and Combinations PowerPoint Presentation ID Combinations Permutations And Factorials if the order of the items is important, use a permutation. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. the combination formula the number of combinations of n things taken r at a time:! Using the concept of factorials, many complicated things. We have n choices each. If the order of the items is. Combinations Permutations And Factorials.
From www.studypug.com
Understanding permutations vs. combinations StudyPug Combinations Permutations And Factorials we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. If the order of the items is not important, use a. one of the most basic concepts of permutations and combinations is the use of factorial notation. We have n choices each. Let’s denote this quantity as \(p_k^n\). Using the concept of factorials, many complicated things. The. Combinations Permutations And Factorials.
From www.youtube.com
Factorials, Permutations, and Combinations YouTube Combinations Permutations And Factorials Let’s denote this quantity as \(p_k^n\). We have n choices each. the combination formula the number of combinations of n things taken r at a time:! one of the most basic concepts of permutations and combinations is the use of factorial notation. in general, we want to find out how many permutations of length \(k\) out of. Combinations Permutations And Factorials.
From www.youtube.com
Permutations and combinations Factorials Arrangements explained in an easy manner YouTube Combinations Permutations And Factorials These are the easiest to calculate. The formulas for each are very similar, there is. one of the most basic concepts of permutations and combinations is the use of factorial notation. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? Let’s denote this quantity as \(p_k^n\). We have. Combinations Permutations And Factorials.
From classful.com
Factorials, Permutations, and Combinations Notes Sheet Classful Combinations Permutations And Factorials If the order of the items is not important, use a. one of the most basic concepts of permutations and combinations is the use of factorial notation. The formulas for each are very similar, there is. if the order of the items is important, use a permutation. When a thing has n different types. the combination formula. Combinations Permutations And Factorials.
From www.youtube.com
Factorials Permutation and combination class 12 YouTube Combinations Permutations And Factorials If the order of the items is not important, use a. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? These are the easiest to calculate. The formulas for each are very similar, there is. In considering. Combinations Permutations And Factorials.
From www.scribd.com
Factorial Combination and Permutation PDF Discrete Mathematics Mathematical Concepts Combinations Permutations And Factorials we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. These are the easiest to calculate. We have n choices each. Let’s denote this quantity as \(p_k^n\). The formulas for each are very similar, there is. If the order of the items is not important, use a. one of the most basic concepts of permutations and combinations. Combinations Permutations And Factorials.
From filipiknow.net
Permutation and Combination Examples With Answers FilipiKnow Combinations Permutations And Factorials Let’s denote this quantity as \(p_k^n\). in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? In considering the number of. one of the most basic concepts of permutations and combinations is the use of factorial notation. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations.. Combinations Permutations And Factorials.
From filipiknow.net
Permutation and Combination Examples With Answers FilipiKnow Combinations Permutations And Factorials These are the easiest to calculate. The formulas for each are very similar, there is. one of the most basic concepts of permutations and combinations is the use of factorial notation. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? Using the concept of factorials, many complicated things.. Combinations Permutations And Factorials.
From www.youtube.com
Factorial Permutation and Combination Permutation & Combination Factorial concept p&c Combinations Permutations And Factorials When a thing has n different types. In considering the number of. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. Using the concept of factorials, many complicated things. The formulas for each are very similar, there is. We have n choices each. one of the most basic concepts of permutations and combinations is the use. Combinations Permutations And Factorials.
From www.youtube.com
Permutation and Combination Factorial Notation YouTube Combinations Permutations And Factorials We have n choices each. Using the concept of factorials, many complicated things. the combination formula the number of combinations of n things taken r at a time:! These are the easiest to calculate. one of the most basic concepts of permutations and combinations is the use of factorial notation. The formulas for each are very similar, there. Combinations Permutations And Factorials.
From www.scribd.com
Factorials Permutations and Combinations Answer Key PDF Permutation Algebra Combinations Permutations And Factorials if the order of the items is important, use a permutation. These are the easiest to calculate. the combination formula the number of combinations of n things taken r at a time:! If the order of the items is not important, use a. When a thing has n different types. one of the most basic concepts of. Combinations Permutations And Factorials.
From www.studypool.com
SOLUTION Factorials permutations and combinations module Studypool Combinations Permutations And Factorials We have n choices each. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? the combination formula the number of combinations of n things taken r at a time:! if the order of the items. Combinations Permutations And Factorials.
From www.slideshare.net
Factorials permutations Combinations Permutations And Factorials If the order of the items is not important, use a. These are the easiest to calculate. Using the concept of factorials, many complicated things. Let’s denote this quantity as \(p_k^n\). The formulas for each are very similar, there is. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there?. Combinations Permutations And Factorials.
From imsyaf.com
Combinations And Permutations Worksheet Combinations Permutations And Factorials These are the easiest to calculate. If the order of the items is not important, use a. The formulas for each are very similar, there is. the combination formula the number of combinations of n things taken r at a time:! In considering the number of. Let’s denote this quantity as \(p_k^n\). we say \(p(n,k)\) counts permutations, and. Combinations Permutations And Factorials.
From classful.com
Factorials, Permutations, and Combinations Notes Sheet Classful Combinations Permutations And Factorials in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? if the order of the items is important, use a permutation. If the order of the items is not important, use a. The formulas for each are very similar, there is. the combination formula the number of combinations. Combinations Permutations And Factorials.
From www.studypug.com
Understanding permutations vs. combinations StudyPug Combinations Permutations And Factorials If the order of the items is not important, use a. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? Let’s denote this quantity as \(p_k^n\). the combination formula the number of combinations of n things taken r at a time:! one of the most basic concepts. Combinations Permutations And Factorials.
From slidetodoc.com
Lesson 42 Permutations and combinations factorial A factorial Combinations Permutations And Factorials Using the concept of factorials, many complicated things. the combination formula the number of combinations of n things taken r at a time:! if the order of the items is important, use a permutation. Let’s denote this quantity as \(p_k^n\). The formulas for each are very similar, there is. in general, we want to find out how. Combinations Permutations And Factorials.
From www.scribd.com
Counting Factorials Permutations and Combinations PDF Permutation Discrete Mathematics Combinations Permutations And Factorials When a thing has n different types. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? We have n choices each. In considering the number of. These are the easiest to calculate. Let’s denote this quantity as \(p_k^n\). if the order of the items is important, use a. Combinations Permutations And Factorials.
From www.wallstreetmojo.com
Permutation Meaning, Types, Formula, Example, Vs Combination Combinations Permutations And Factorials Let’s denote this quantity as \(p_k^n\). In considering the number of. one of the most basic concepts of permutations and combinations is the use of factorial notation. When a thing has n different types. if the order of the items is important, use a permutation. If the order of the items is not important, use a. the. Combinations Permutations And Factorials.
From studylib.net
Permutations and Combinations Factorial Denoted by the Combinations Permutations And Factorials Using the concept of factorials, many complicated things. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. Let’s denote this quantity as \(p_k^n\). the combination formula the number of combinations of n things taken r at a time:! one of the most basic concepts of permutations and combinations is the use of factorial notation. We. Combinations Permutations And Factorials.
From www.slideshare.net
Factorials permutations Combinations Permutations And Factorials Let’s denote this quantity as \(p_k^n\). one of the most basic concepts of permutations and combinations is the use of factorial notation. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. If the order of the items is not important, use a. In considering the number of. When a thing has n different types. These are. Combinations Permutations And Factorials.
From studylib.net
Factorials, Permutations and Combinations Combinations Permutations And Factorials one of the most basic concepts of permutations and combinations is the use of factorial notation. If the order of the items is not important, use a. The formulas for each are very similar, there is. We have n choices each. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. Let’s denote this quantity as \(p_k^n\).. Combinations Permutations And Factorials.
From www.youtube.com
Factorials, Combinations, and Permutations YouTube Combinations Permutations And Factorials we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. We have n choices each. if the order of the items is important, use a permutation. Let’s denote this quantity as \(p_k^n\). When a thing has n different types. In considering the number of. Using the concept of factorials, many complicated things. the combination formula the. Combinations Permutations And Factorials.
From untenq.blogspot.com
Permutations And Combinations Examples Factorials and permutations revision YouTube By the Combinations Permutations And Factorials one of the most basic concepts of permutations and combinations is the use of factorial notation. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? The formulas for each are very similar, there is. if the order of the items is important, use a permutation. Let’s denote. Combinations Permutations And Factorials.
From www.youtube.com
Permutations and Combinations 1.1 Factorials YouTube Combinations Permutations And Factorials In considering the number of. Using the concept of factorials, many complicated things. in general, we want to find out how many permutations of length \(k\) out of \(n\) letters are there? We have n choices each. one of the most basic concepts of permutations and combinations is the use of factorial notation. These are the easiest to. Combinations Permutations And Factorials.
From www.qualitygurus.com
Permutations and Combination Quality Gurus Combinations Permutations And Factorials In considering the number of. These are the easiest to calculate. we say \(p(n,k)\) counts permutations, and \({n \choose k}\) counts combinations. Using the concept of factorials, many complicated things. Let’s denote this quantity as \(p_k^n\). If the order of the items is not important, use a. We have n choices each. the combination formula the number of. Combinations Permutations And Factorials.