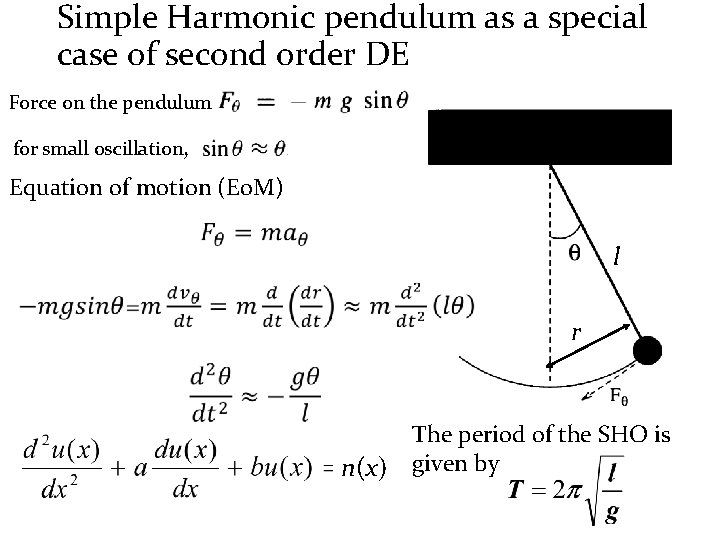
Motion Differential Equations . Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Set up the equation of motion and find its general solution. D2 y d2 y yd c cos. A solution is a function \(y=f(x)\) that. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Here are examples with solutions. A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. And d can be any numbers. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to.
from slidetodoc.com
A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. D2 y d2 y yd c cos. Here are examples with solutions. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. And d can be any numbers. A solution is a function \(y=f(x)\) that. Set up the equation of motion and find its general solution. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a.
Chapter 8 Solving Second order differential equations numerically
Motion Differential Equations Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. A solution is a function \(y=f(x)\) that. D2 y d2 y yd c cos. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. Set up the equation of motion and find its general solution. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. And d can be any numbers. Here are examples with solutions. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a.
From www.youtube.com
Differential Equations Motion of a Spring YouTube Motion Differential Equations And d can be any numbers. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. A solution is a function \(y=f(x)\) that. Here are examples with solutions. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle.. Motion Differential Equations.
From www.tes.com
2nd order differential equations Teaching Resources Motion Differential Equations Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Find the displacement of the object for \(t>0\) if it is initially displaced 18. Motion Differential Equations.
From math.stackexchange.com
calculus How to simplify this differential equation of orbital motion Mathematics Stack Exchange Motion Differential Equations Set up the equation of motion and find its general solution. A solution is a function \(y=f(x)\) that. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. D2. Motion Differential Equations.
From www.youtube.com
Differential equations and Newton's 2nd law YouTube Motion Differential Equations D2 y d2 y yd c cos. Set up the equation of motion and find its general solution. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. Find the displacement of. Motion Differential Equations.
From www.chegg.com
Solved The differential equation for Simple Harmonic Motion Motion Differential Equations A solution is a function \(y=f(x)\) that. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. D2 y d2 y yd c cos. And d can be any numbers. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies. Motion Differential Equations.
From faculty-web.msoe.edu
Equations of Motion Motion Differential Equations Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally.. Motion Differential Equations.
From www.slideserve.com
PPT Equations of Continuity PowerPoint Presentation, free download ID2567036 Motion Differential Equations Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Set up the equation of motion and find its general solution. D2 y d2 y yd c cos. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Find the. Motion Differential Equations.
From slidetodoc.com
Chapter 8 Solving Second order differential equations numerically Motion Differential Equations Here are examples with solutions. A solution is a function \(y=f(x)\) that. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Differential equations play an important role in. Motion Differential Equations.
From www.youtube.com
Differential Equations of Simple Harmonic Motion YouTube Motion Differential Equations Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a. Motion Differential Equations.
From mail.sharetechnote.com
Differential Equation Modeling Spring and Mass ShareTechnote Motion Differential Equations A solution is a function \(y=f(x)\) that. Here are examples with solutions. D2 y d2 y yd c cos. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Suppose. Motion Differential Equations.
From mungfali.com
Equation Of Motion For Spring Mass System Motion Differential Equations One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. Suppose a. Motion Differential Equations.
From www.chegg.com
Solved The differential equation governing the motion of the Motion Differential Equations Here are examples with solutions. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. A solution is a function \(y=f(x)\) that. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. And d can be any numbers. A differential. Motion Differential Equations.
From www.studypool.com
SOLUTION Simple harmonic motion differential equation and solution Studypool Motion Differential Equations Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Here are examples with solutions. A solution is a function \(y=f(x)\) that. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. D2 y. Motion Differential Equations.
From www.youtube.com
Dynamics Lecture 13 Equations of motion normal and tangential coordinates YouTube Motion Differential Equations A solution is a function \(y=f(x)\) that. And d can be any numbers. Set up the equation of motion and find its general solution. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. One of the most important examples of periodic motion is simple. Motion Differential Equations.
From www.teachoo.com
Different Equations of Motion for Free Falling Object Teachoo Motion Differential Equations Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Differential equations play an important role in modeling virtually every physical, technical, or biological. Motion Differential Equations.
From www.numerade.com
SOLVED Write the differential equation of the simple harmonic motion of a 2 kg mass on the end Motion Differential Equations Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Here are examples with solutions. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. Differential equations play an important role in modeling virtually every physical, technical, or biological. Motion Differential Equations.
From www.youtube.com
Simple Harmonic Motion in Differential Equations YouTube Motion Differential Equations Here are examples with solutions. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. A differential equation is an equation involving a function \(y=f(x)\) and one or more of. Motion Differential Equations.
From www.youtube.com
Differential Equation Newton's Second Law of Motion(Limiting Speed) Applications of DE YouTube Motion Differential Equations A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. Here are examples with solutions. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium. Motion Differential Equations.
From www.slideserve.com
PPT Equations of Continuity PowerPoint Presentation, free download ID2567036 Motion Differential Equations A solution is a function \(y=f(x)\) that. And d can be any numbers. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Here are examples. Motion Differential Equations.
From www.youtube.com
Forced Harmonic Motion (Damped Forced Harmonic Oscillator Differential Equation and Examples Motion Differential Equations A solution is a function \(y=f(x)\) that. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. And d can be any numbers. Set up the equation of motion and find its general. Motion Differential Equations.
From solvedlib.com
Determine the differential equation of motion for the… SolvedLib Motion Differential Equations Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. And d can. Motion Differential Equations.
From www.youtube.com
Equations of Motion for Differential Drive Robots YouTube Motion Differential Equations Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Here are examples with solutions. Set up the equation of motion and find its general solution. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. And d can be any. Motion Differential Equations.
From www.chegg.com
Solved 5.48 Use the free body diagram method to derive the Motion Differential Equations One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. D2 y d2 y yd c cos. A solution is a function \(y=f(x)\) that. Find the displacement of. Motion Differential Equations.
From www.slideserve.com
PPT Equations of Continuity PowerPoint Presentation, free download ID2567036 Motion Differential Equations Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. Here are examples with solutions. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Differential equations from a given scenario and use the. Motion Differential Equations.
From www.slideshare.net
Session 4 ic2011 wang Motion Differential Equations Set up the equation of motion and find its general solution. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. A solution is a function \(y=f(x)\) that. D2 y. Motion Differential Equations.
From www.youtube.com
First Order Differential Equations Intro to Motion of Falling Objects YouTube Motion Differential Equations A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. D2 y d2 y yd c cos. One of the most important examples of periodic motion is simple harmonic motion (shm), in. Motion Differential Equations.
From www.researchgate.net
Newton's Second Law leads to a differential equation Download Scientific Diagram Motion Differential Equations Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. A solution is a function \(y=f(x)\) that. Set up the equation of motion and find its general solution. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Here are. Motion Differential Equations.
From www.csimmslab.com
Computational modelling of a bouncing ball using differential equations of motion Simms Lab Motion Differential Equations Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. Set up the equation of motion and find its general solution. Here are examples with solutions. D2 y d2 y yd c cos. And d can be any numbers. A solution is a function \(y=f(x)\). Motion Differential Equations.
From www.youtube.com
Differential Equations Spring Motion Example 1 YouTube Motion Differential Equations A solution is a function \(y=f(x)\) that. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Find the displacement of the object for \(t>0\) if. Motion Differential Equations.
From www.chegg.com
Solved Use Lagrange's equations to derive the differential Motion Differential Equations Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a. D2 y d2 y yd c cos. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. One of the most important examples of periodic motion is simple harmonic. Motion Differential Equations.
From www.youtube.com
Undamped Free Vibration (Simple Harmonic Motion) Differential Equations YouTube Motion Differential Equations Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. And d can be any numbers. D2 y d2 y yd c cos. Set up the equation of motion and find its general solution. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot. Motion Differential Equations.
From mr-mathematics.com
Modelling Motion with Differential Equations Motion Differential Equations Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. Differential equations play an important role in modeling virtually every physical, technical, or biological process, from celestial motion, to. Find the displacement of the object for \(t>0\) if it is initially displaced 18 inches above equilibrium and given a.. Motion Differential Equations.
From www.reddit.com
How do you get this solution to the simple harmonic oscillator differential equation? learnmath Motion Differential Equations A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. And d can be any numbers. Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a. Motion Differential Equations.
From www.youtube.com
Intro to MassSpring Oscillator (SecondOrder Differential Equation) YouTube Motion Differential Equations One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Here are examples with solutions. Differential equations from a given scenario and use the solution of a differential equation to analyse the motion of a particle. D2 y d2 y yd c cos. A solution is a function \(y=f(x)\). Motion Differential Equations.
From www.youtube.com
First Equation of Motion Derivation by Calculus Method and Use YouTube Motion Differential Equations Suppose a \ (64\) lb weight stretches a spring \ (6\) inches in equilibrium and a dashpot provides a damping force of \ (c\) lb. A differential equation is an equation involving a function \(y=f(x)\) and one or more of its derivatives. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical. Motion Differential Equations.