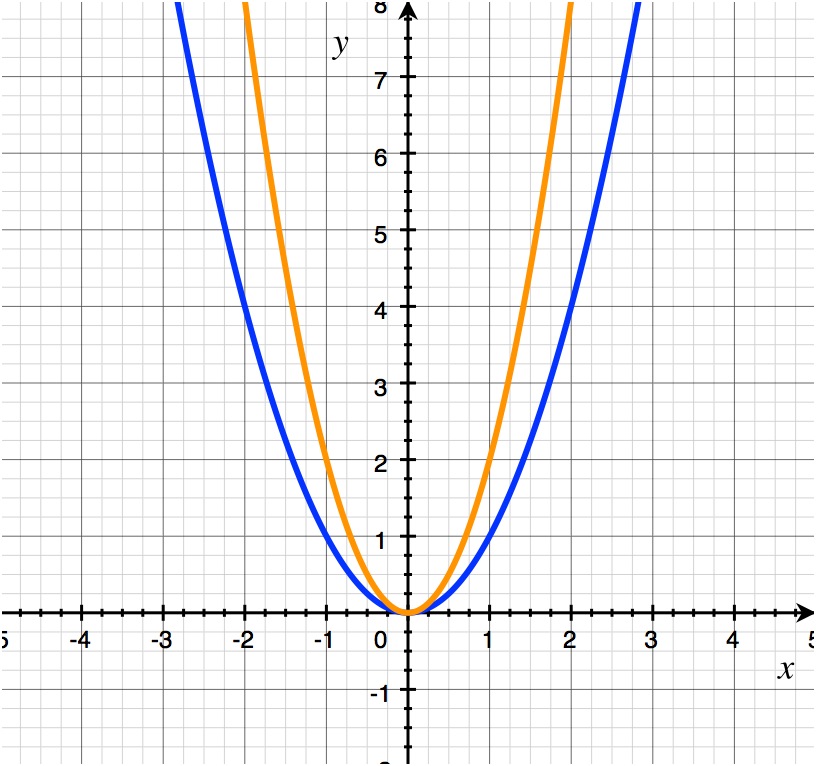
Compression In Graph . Adding a constant to the inputs or outputs of a function changed the position of a. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Graphing functions using stretches and compressions. Graph functions using compressions and stretches. Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function.
from thenumerist.com
When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Graph functions using compressions and stretches. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Graphing functions using stretches and compressions. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. Just like transformations in geometry, we can move and resize the graphs of functions. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Adding a constant to the inputs or outputs of a function changed the position of a.
Stretching Graphs and Compressing Graphs
Compression In Graph Graph functions using compressions and stretches. Graphing functions using stretches and compressions. Graph functions using compressions and stretches. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Adding a constant to the inputs or outputs of a function changed the position of a. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Just like transformations in geometry, we can move and resize the graphs of functions.
From physics.stackexchange.com
Why is the centre of compression different for two different graphs of Compression In Graph Just like transformations in geometry, we can move and resize the graphs of functions. Adding a constant to the inputs or outputs of a function changed the position of a. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Adding a constant to the inputs or outputs of a function changed the position of a graph with. Compression In Graph.
From byjus.com
Explain the phenomena of propagation of sound wave through compressions Compression In Graph Adding a constant to the inputs or outputs of a function changed the position of a. Graphing functions using stretches and compressions. Graph functions using compressions and stretches. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to. Compression In Graph.
From msestudent.com
Stress, Strain, and the StressStrain Curve Materials Science Compression In Graph If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Adding a constant to the inputs or outputs of a function changed the position of a. Just like transformations in geometry, we can move and resize the graphs of functions. This tells us that we need to divide each of the \ (x\) coordinates on the graph by. Compression In Graph.
From boneandjoint.org.uk
Standardizing compression testing for measuring the stiffness of human Compression In Graph Graphing functions using stretches and compressions. Adding a constant to the inputs or outputs of a function changed the position of a. Just like transformations in geometry, we can move and resize the graphs of functions. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Graph functions using compressions and stretches. When we multiply a function by. Compression In Graph.
From www.emathinstruction.com
Vertical Stretching and Compressing of Functions eMATHinstruction Compression In Graph When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Adding a constant to the inputs or outputs of a function changed the position of a. Graph functions using compressions and stretches. This tells us that we need to divide each. Compression In Graph.
From www.emathinstruction.com
Vertical Stretching and Compressing of Functions eMATHinstruction Compression In Graph This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Just like transformations in geometry, we can move and resize the graphs of functions. Graphing functions using stretches and compressions. Graph functions using compressions and stretches. Adding a constant to the inputs or outputs of. Compression In Graph.
From www4.uwsp.edu
Lecture 38 Compression In Graph Just like transformations in geometry, we can move and resize the graphs of functions. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Graph functions using compressions and stretches. Graphing functions using. Compression In Graph.
From www.expii.com
Square Root Function Graph Examples & Practice Expii Compression In Graph Graph functions using compressions and stretches. Adding a constant to the inputs or outputs of a function changed the position of a. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. This tells us that we need to divide each of the. Compression In Graph.
From study.com
Stretching & Compressing a Function Video & Lesson Transcript Compression In Graph This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Just like transformations in geometry, we can move and resize the graphs of functions. Graph functions using compressions and stretches. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Graphing functions using. Compression In Graph.
From www.eigenplus.com
Isothermal process Definition, Work done & Explanation eigenplus Compression In Graph Just like transformations in geometry, we can move and resize the graphs of functions. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Adding a constant to the inputs or outputs of a function changed the position of a. Graph functions using compressions and. Compression In Graph.
From www.youtube.com
Determine a Vertical Stretch or Vertical Compression YouTube Compression In Graph This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Graph functions using compressions and stretches. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. If \. Compression In Graph.
From www.youtube.com
Math 10 6.4 Graphing Stretches and Compressions YouTube Compression In Graph Graph functions using compressions and stretches. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Graphing functions using stretches and compressions. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but. Compression In Graph.
From www.youtube.com
Functions Stretching, Compressing, and Reflecting Functions YouTube Compression In Graph If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Graphing functions using stretches and compressions. Just like transformations in geometry, we can move and resize the graphs of functions. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. Graph. Compression In Graph.
From www.easysevens.com
Transformation of Functions and Graphs Easy Sevens Education Compression In Graph Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. Adding a constant to the inputs or outputs of a function changed the position of a. Graph functions using compressions and stretches. Just like transformations in geometry, we can move and resize the. Compression In Graph.
From www.researchgate.net
Compression force displacement graphs of the composites. Download Compression In Graph When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Graphing functions using stretches and compressions. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Adding a constant to the inputs or outputs of a function changed the. Compression In Graph.
From ar.inspiredpencil.com
Compression Force Diagram Compression In Graph Just like transformations in geometry, we can move and resize the graphs of functions. Graphing functions using stretches and compressions. Graph functions using compressions and stretches. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Adding a constant to the. Compression In Graph.
From www.youtube.com
Vertical Stretch and Compression using Absolute Value YouTube Compression In Graph Graphing functions using stretches and compressions. Graph functions using compressions and stretches. Just like transformations in geometry, we can move and resize the graphs of functions. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. If \ (f (x) = x^2\), then. Compression In Graph.
From www.youtube.com
Horizontal Stretch and Compression YouTube Compression In Graph Graphing functions using stretches and compressions. Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. This tells us that we need to divide each of the. Compression In Graph.
From www.researchgate.net
Stressstrain relationship for wood under tension and compression Compression In Graph Graphing functions using stretches and compressions. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Just like. Compression In Graph.
From www.tec-science.com
Compression test tecscience Compression In Graph Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. When we multiply a function by a positive. Compression In Graph.
From www.youtube.com
Determine a Horizontal Stretch or Horizontal Compression YouTube Compression In Graph This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. Just like transformations in geometry, we can move. Compression In Graph.
From en.neurochispas.com
Stretches and Compressions of Functions with Examples Neurochispas Compression In Graph When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Adding a constant to the inputs. Compression In Graph.
From learncheme.com
LearnChemE Compression In Graph Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. Graphing functions using stretches and compressions. Just like transformations in geometry, we can move and resize the graphs of functions. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Graph. Compression In Graph.
From www.onlinemathlearning.com
Manipulating Graphs Shifts and Stretches (examples, solutions Compression In Graph Adding a constant to the inputs or outputs of a function changed the position of a. Graphing functions using stretches and compressions. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Graph. Compression In Graph.
From www.youtube.com
Ex Identify Horizontal and Vertical Stretches and Compressions Compression In Graph This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in. Compression In Graph.
From www.slideserve.com
PPT 3.4 Graphs and Transformations PowerPoint Presentation, free Compression In Graph Graphing functions using stretches and compressions. Graph functions using compressions and stretches. Adding a constant to the inputs or outputs of a function changed the position of a. If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by. Compression In Graph.
From www.garagelube.com
WPS500X Compression Test graphs internal cylinder pressure Compression In Graph Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. If \ (f (x) = x^2\), then \. Compression In Graph.
From www.researchgate.net
Compression test results of (a) EG gels and (b) hydrogels and cyclic Compression In Graph When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. If \ (f (x) = x^2\),. Compression In Graph.
From www.themathdoctors.org
Shifting and Stretching Graphs The Math Doctors Compression In Graph If \ (f (x) = x^2\), then \ (f (ax) = (ax)^2\). Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Adding a constant to the. Compression In Graph.
From www.slideserve.com
PPT Sampling in Graphs PowerPoint Presentation, free download ID Compression In Graph This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Graphing functions using stretches and compressions. Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function whose graph. Compression In Graph.
From www.uaudio.com
Audio Compression Basics Universal Audio Compression In Graph Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. Graph functions using compressions and stretches. If \ (f (x) = x^2\), then \ (f (ax) =. Compression In Graph.
From thenumerist.com
Stretching Graphs and Compressing Graphs Compression In Graph Graph functions using compressions and stretches. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the. Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function whose graph. Compression In Graph.
From courses.lumenlearning.com
Stretching, Compressing, or Reflecting a Logarithmic Function College Compression In Graph Graphing functions using stretches and compressions. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. Just like transformations in geometry, we can move and resize the graphs of functions. When we multiply a function by a positive constant, we get a function. Compression In Graph.
From www.chegg.com
Solved Question 2 F (N) x (m) An object is pushed into a Compression In Graph Graph functions using compressions and stretches. Adding a constant to the inputs or outputs of a function changed the position of a. Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, but it did not affect. If \ (f (x) = x^2\), then \ (f (ax) =. Compression In Graph.
From www.pinterest.com
Vertical Vertical, Compression, Chart Compression In Graph Graph functions using compressions and stretches. When we multiply a function by a positive constant, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. This tells us that we need to divide each of the \ (x\) coordinates on the graph by \ (a\) in order to compress the.. Compression In Graph.