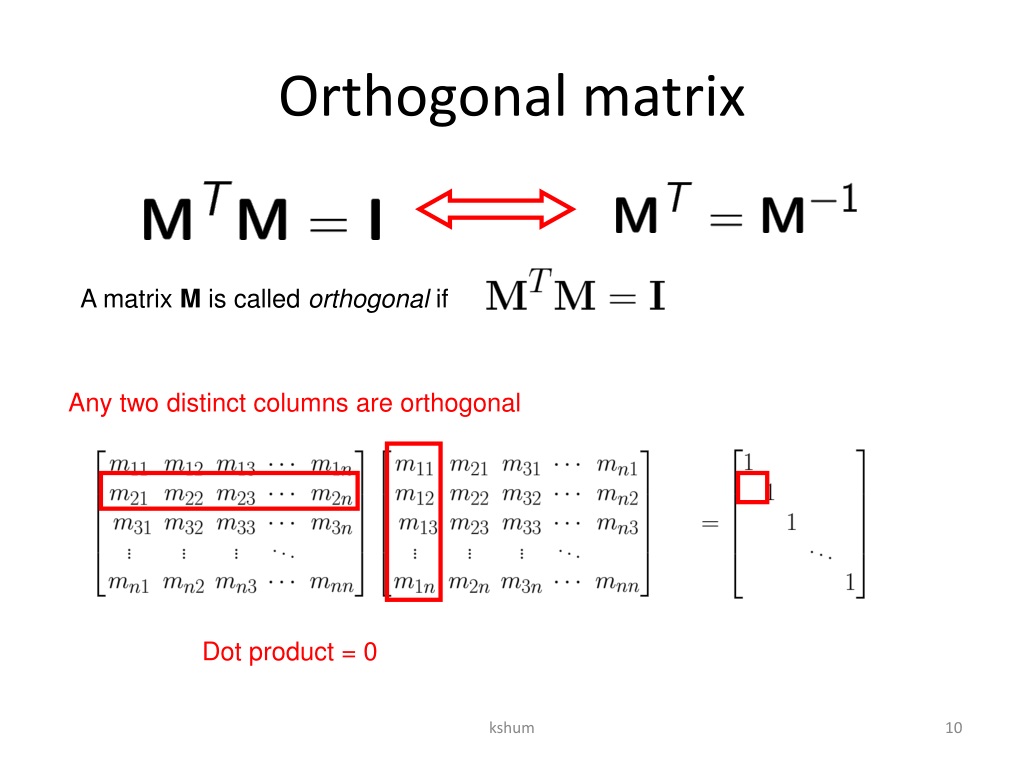
Condition For A Matrix To Be Orthogonal . A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Learn more about the orthogonal. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. In other words, the columns of the matrix form a collection of. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. Also, the product of an orthogonal matrix and its transpose is equal to i. Every two rows and two columns have a dot. That is, the following condition is met: Where a is an orthogonal matrix and a t is its transpose. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions:
from www.slideserve.com
For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. Also, the product of an orthogonal matrix and its transpose is equal to i. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Where a is an orthogonal matrix and a t is its transpose. Every two rows and two columns have a dot. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: In other words, the columns of the matrix form a collection of. That is, the following condition is met:
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint
Condition For A Matrix To Be Orthogonal Where a is an orthogonal matrix and a t is its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. Every two rows and two columns have a dot. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. That is, the following condition is met: In other words, the columns of the matrix form a collection of.
From www.toppr.com
An orthogonal matrix is Maths Questions Condition For A Matrix To Be Orthogonal For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. In other words, the columns of the matrix form a collection of. Every two. Condition For A Matrix To Be Orthogonal.
From www.chegg.com
Solved a. Which of the matrices are orthogonal (has Condition For A Matrix To Be Orthogonal Where a is an orthogonal matrix and a t is its transpose. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. That is, the following condition is met: Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. In other words, the columns of the matrix form a collection of.. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Condition For A Matrix To Be Orthogonal Where a is an orthogonal matrix and a t is its transpose. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. Learn more about the orthogonal. Every two rows and two columns have a dot. In other words, the columns of the matrix form a collection of. A n×n matrix a is an. Condition For A Matrix To Be Orthogonal.
From www.slideserve.com
PPT Row and column matrices are sometimes called row vectors and Condition For A Matrix To Be Orthogonal A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. That is, the following condition is met: Where a is an orthogonal matrix and a t is its transpose. Formally,. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
How to prove ORTHOGONAL Matrices YouTube Condition For A Matrix To Be Orthogonal For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: That is, the following condition is met: Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. A n×n matrix a is. Condition For A Matrix To Be Orthogonal.
From www.slideserve.com
PPT 6.4 Best Approximation; Least Squares PowerPoint Presentation Condition For A Matrix To Be Orthogonal Also, the product of an orthogonal matrix and its transpose is equal to i. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. In other words, the columns of the matrix form a collection of. That is, the following condition is. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
Orthogonal Matrix example YouTube Condition For A Matrix To Be Orthogonal A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Every two rows and two columns have a dot. Where a is an orthogonal matrix and a t is its transpose. A matrix 'a' is orthogonal if and only if its inverse is equal to its. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix Important Questions on Condition For A Matrix To Be Orthogonal That is, the following condition is met: Learn more about the orthogonal. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. In other words, the columns of the matrix form a collection of. For any matrix to be an orthogonal matrix, it needs to fulfil. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
Properties of Orthogonal Matrix Example1 YouTube Condition For A Matrix To Be Orthogonal Where a is an orthogonal matrix and a t is its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. That is, the following condition is met: A. Condition For A Matrix To Be Orthogonal.
From oneclass.com
OneClass Determine whether the given matrix is orthogonal. 12 3 4 The Condition For A Matrix To Be Orthogonal For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: In other words, the columns of the matrix form a collection of. Learn more about the. Condition For A Matrix To Be Orthogonal.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint Condition For A Matrix To Be Orthogonal Learn more about the orthogonal. In other words, the columns of the matrix form a collection of. Every two rows and two columns have a dot. That is, the following condition is met: A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For a square matrix 𝐴 to be orthogonal, it must be. Condition For A Matrix To Be Orthogonal.
From www.slideserve.com
PPT Orthogonal matrices PowerPoint Presentation, free download ID Condition For A Matrix To Be Orthogonal For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A matrix 'a' is orthogonal if and. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
Orthonormal,Orthogonal matrix (EE MATH มทส.) YouTube Condition For A Matrix To Be Orthogonal Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. Also, the product of an orthogonal matrix and its transpose is equal to i. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Where a is an orthogonal matrix and a t is its transpose. For this condition to be. Condition For A Matrix To Be Orthogonal.
From slidetodoc.com
Chapter Content n n n Eigenvalues and Eigenvectors Condition For A Matrix To Be Orthogonal A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Learn more about the orthogonal. Every two rows and two columns have a dot. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴. Condition For A Matrix To Be Orthogonal.
From www.chegg.com
Solved Orthogonal Transformations & Orthogonal Matrices In Condition For A Matrix To Be Orthogonal Learn more about the orthogonal. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴. Condition For A Matrix To Be Orthogonal.
From www.chegg.com
Solved Orthogonally diagonalize the matrix, giving an Condition For A Matrix To Be Orthogonal That is, the following condition is met: A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Learn more about the orthogonal. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. For this condition to be fulfilled, the columns and rows of. Condition For A Matrix To Be Orthogonal.
From youtube.com
1.3 Orthogonal Vectors YouTube Condition For A Matrix To Be Orthogonal Where a is an orthogonal matrix and a t is its transpose. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. Also, the product of an orthogonal matrix and its transpose is equal to i. Every two rows and two. Condition For A Matrix To Be Orthogonal.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Condition For A Matrix To Be Orthogonal In other words, the columns of the matrix form a collection of. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. That is, the. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube Condition For A Matrix To Be Orthogonal Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix. Condition For A Matrix To Be Orthogonal.
From www.numerade.com
SOLVED Consider the matrix Find a basis of the orthogonal complement Condition For A Matrix To Be Orthogonal Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. Where a is an orthogonal matrix and a t is its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A matrix 'a' is orthogonal if and only if its inverse. Condition For A Matrix To Be Orthogonal.
From medium.com
[Linear Algebra] 9. Properties of orthogonal matrices by jun94 jun Condition For A Matrix To Be Orthogonal For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. That is, the following condition is met: For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: Every two rows and two columns have a dot. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t). Condition For A Matrix To Be Orthogonal.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Condition For A Matrix To Be Orthogonal A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Every two rows and two columns have a dot. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. A matrix 'a' is orthogonal if and only if its inverse is equal to. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
MATRICES (L3) LINEAR TRANSFORMATIONORTHOGONAL MATRIX YouTube Condition For A Matrix To Be Orthogonal Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. For a square matrix 𝐴 to be orthogonal, it must be the case. Condition For A Matrix To Be Orthogonal.
From ar.inspiredpencil.com
Orthogonal Matrix Condition For A Matrix To Be Orthogonal Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: In other words, the columns of the matrix form a collection of. Learn more about the. Condition For A Matrix To Be Orthogonal.
From ar.inspiredpencil.com
3x3 Orthogonal Matrix Condition For A Matrix To Be Orthogonal Learn more about the orthogonal. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. Every two rows and two columns have a dot. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: That is,. Condition For A Matrix To Be Orthogonal.
From www.chegg.com
Solved Consider the matrixFind the orthogonal complement of Condition For A Matrix To Be Orthogonal Also, the product of an orthogonal matrix and its transpose is equal to i. Where a is an orthogonal matrix and a t is its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. That is, the following condition is met: For any matrix. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Condition For A Matrix To Be Orthogonal A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Formally, a matrix $a$ is called orthogonal if $a^ta = aa^t = i$. Also, the product of an orthogonal matrix and its transpose is equal to i. That is, the following condition is met: Where a. Condition For A Matrix To Be Orthogonal.
From www.youtube.com
Orthogonal Matrix With Definition, Example and Properties YouTube Condition For A Matrix To Be Orthogonal Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: Formally, a matrix $a$. Condition For A Matrix To Be Orthogonal.
From www.coursehero.com
[Solved] . Find an orthogonal basis for the column space of the matrix Condition For A Matrix To Be Orthogonal For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. Where a is an orthogonal matrix and a t is its transpose. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. A matrix 'a'. Condition For A Matrix To Be Orthogonal.
From www.chegg.com
Solved I. (a) Under what conditions on the real numbers α Condition For A Matrix To Be Orthogonal A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. That is, the following condition is met: In other words, the columns of the matrix form a collection of. Where a is an orthogonal matrix and a t is its transpose. For a square matrix 𝐴 to be orthogonal, it must be the case. Condition For A Matrix To Be Orthogonal.
From www.slideshare.net
Orthogonal porjection in statistics Condition For A Matrix To Be Orthogonal A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. That is, the following condition is met: For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: A n×n matrix a is an. Condition For A Matrix To Be Orthogonal.
From www.chegg.com
Solved Orthogonally diagonalize the matrix below, giving an Condition For A Matrix To Be Orthogonal A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. For a square matrix 𝐴 to be orthogonal, it must be the case that 𝐴 𝐴 = 𝐼, where 𝐴 is the matrix transpose of 𝐴 and where 𝐼. Every two rows and two columns have. Condition For A Matrix To Be Orthogonal.
From datingluda.weebly.com
Orthogonal matrix datingluda Condition For A Matrix To Be Orthogonal In other words, the columns of the matrix form a collection of. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. A matrix 'a' is orthogonal if and. Condition For A Matrix To Be Orthogonal.
From ar.inspiredpencil.com
3x3 Orthogonal Matrix Condition For A Matrix To Be Orthogonal For any matrix to be an orthogonal matrix, it needs to fulfil the following conditions: Every two rows and two columns have a dot. Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. For this condition to be fulfilled, the columns and rows of an orthogonal matrix must be. That is, the. Condition For A Matrix To Be Orthogonal.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Condition For A Matrix To Be Orthogonal Every two rows and two columns have a dot. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Learn more about the orthogonal. Where a is an orthogonal matrix and a t is its transpose. For any matrix to be an orthogonal matrix, it needs. Condition For A Matrix To Be Orthogonal.