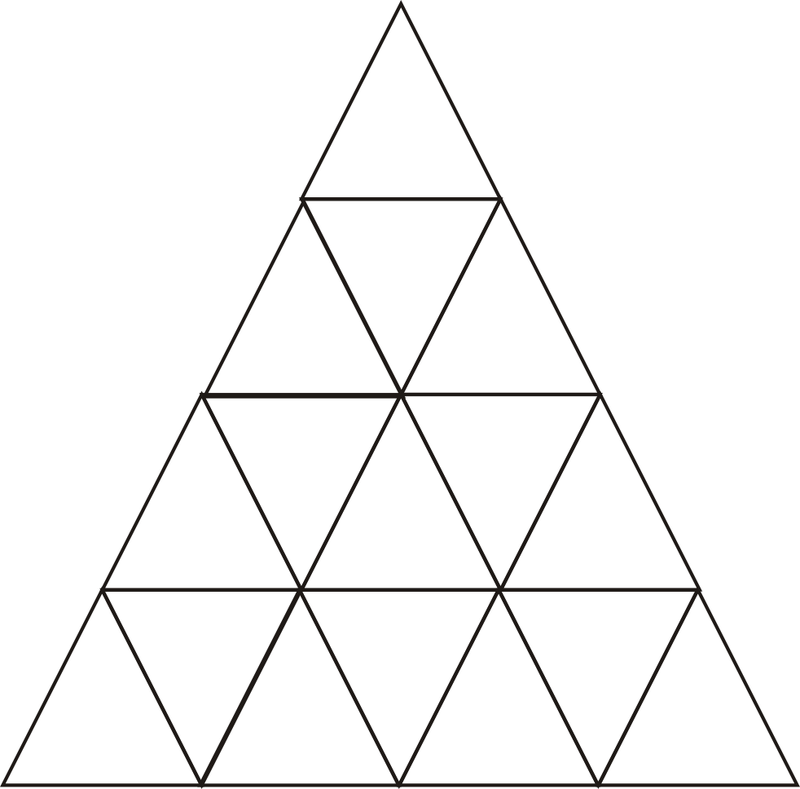
How Many Triangles In Diagram . Is there any other way to count the no. Previous video in this series:. I have manually counted the no of triangles in the diagram. How many triangles are there in the figure? To obtain a recurssion formula for the $t_n$ we have to. I want to count the number of triangle in the following diagram. In the following examples you can see it in detail. If the given figure has only one square or rectangle, then the formula to find the number of triangles is. Number of diagonals ⋅ number of blocks. Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): In this article provides the simple tricks with formulas to find the number of triangles for the following figures. Let s(n) be the number of triangle for n floors: The star has $5$ vertices, hence: How many triangles are there in this diagram? The no of triangles is 44.
from www.ck12.org
Previous video in this series:. I have manually counted the no of triangles in the diagram. How many triangles are there in this diagram? Let s(n) be the number of triangle for n floors: If it has combination of more than one squares, we have to mark the spot where it joins. I want to count the number of triangle in the following diagram. The no of triangles is 44. Is there any other way to count the no. In the following examples you can see it in detail. To obtain a recurssion formula for the $t_n$ we have to.
Classifying Polygons CK12 Foundation
How Many Triangles In Diagram Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): Previous video in this series:. Number of diagonals ⋅ number of blocks. The no of triangles is 44. How many triangles are there in the figure? How many triangles are there in this diagram? Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. To obtain a recurssion formula for the $t_n$ we have to. In the following examples you can see it in detail. In this article provides the simple tricks with formulas to find the number of triangles for the following figures. Is there any other way to count the no. Let s(n) be the number of triangle for n floors: If the given figure has only one square or rectangle, then the formula to find the number of triangles is. The star has $5$ vertices, hence: I have manually counted the no of triangles in the diagram.
From www.gkblogs.com
How Many Triangles Are In this Picture How Many Triangles In Diagram If the given figure has only one square or rectangle, then the formula to find the number of triangles is. How many triangles are there in the figure? Is there any other way to count the no. I want to count the number of triangle in the following diagram. The star has $5$ vertices, hence: If it has combination of. How Many Triangles In Diagram.
From quizlet.com
Triangles (math) Diagram Quizlet How Many Triangles In Diagram Let s(n) be the number of triangle for n floors: I want to count the number of triangle in the following diagram. How many triangles are there in the figure? If it has combination of more than one squares, we have to mark the spot where it joins. If the given figure has only one square or rectangle, then the. How Many Triangles In Diagram.
From www.cuemath.com
Triangles Definition, Properties, Formula Triangle Shape How Many Triangles In Diagram In this article provides the simple tricks with formulas to find the number of triangles for the following figures. I have manually counted the no of triangles in the diagram. If the given figure has only one square or rectangle, then the formula to find the number of triangles is. If it has combination of more than one squares, we. How Many Triangles In Diagram.
From e-gmat.com
Properties of Triangle types & formulas [Video & Practice] How Many Triangles In Diagram The no of triangles is 44. Let s(n) be the number of triangle for n floors: If it has combination of more than one squares, we have to mark the spot where it joins. In the following examples you can see it in detail. I have manually counted the no of triangles in the diagram. The star has $5$ vertices,. How Many Triangles In Diagram.
From www.rd.com
How Many Triangles Do You See? Learn the Answer Reader's Digest How Many Triangles In Diagram Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): Is there any other way to count the no. Let s(n) be the number of triangle for n floors: Previous video in this series:. How many triangles are there in this diagram? If it has combination of more than one squares, we. How Many Triangles In Diagram.
From exordchwc.blob.core.windows.net
How Many Triangles Are There In This Diagram at Amy Blevins blog How Many Triangles In Diagram The star has $5$ vertices, hence: If the given figure has only one square or rectangle, then the formula to find the number of triangles is. I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. Is there any other way to count the no. In this. How Many Triangles In Diagram.
From www.toppr.com
How many triangles are there in the following figure How Many Triangles In Diagram If it has combination of more than one squares, we have to mark the spot where it joins. I want to count the number of triangle in the following diagram. In the following examples you can see it in detail. The no of triangles is 44. To obtain a recurssion formula for the $t_n$ we have to. Is there any. How Many Triangles In Diagram.
From www.youtube.com
How Many Triangles Are There? Learn The Formula For Any Size! YouTube How Many Triangles In Diagram Previous video in this series:. In the following examples you can see it in detail. How many triangles are there in the figure? Number of diagonals ⋅ number of blocks. I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. If the given figure has only one. How Many Triangles In Diagram.
From e-gmat.com
Properties of Triangle types & formulas [Video & Practice] How Many Triangles In Diagram To obtain a recurssion formula for the $t_n$ we have to. In the following examples you can see it in detail. Number of diagonals ⋅ number of blocks. The star has $5$ vertices, hence: If the given figure has only one square or rectangle, then the formula to find the number of triangles is. The no of triangles is 44.. How Many Triangles In Diagram.
From quizlet.com
How many triangles are in the following figure? Quizlet How Many Triangles In Diagram The no of triangles is 44. To obtain a recurssion formula for the $t_n$ we have to. Number of diagonals ⋅ number of blocks. In the following examples you can see it in detail. Is there any other way to count the no. I have manually counted the no of triangles in the diagram. I want to count the number. How Many Triangles In Diagram.
From www.mathswithgraham.org.uk
How many triangles Maths with Graham How Many Triangles In Diagram Previous video in this series:. To obtain a recurssion formula for the $t_n$ we have to. If it has combination of more than one squares, we have to mark the spot where it joins. I have manually counted the no of triangles in the diagram. I looked by recurrence at how many triangles are added when moving from k to. How Many Triangles In Diagram.
From study.com
Types of Triangles & Their Properties Lesson How Many Triangles In Diagram In this article provides the simple tricks with formulas to find the number of triangles for the following figures. If it has combination of more than one squares, we have to mark the spot where it joins. I have manually counted the no of triangles in the diagram. The no of triangles is 44. Each vertex of the star can. How Many Triangles In Diagram.
From donsteward.blogspot.co.uk
MEDIAN Don Steward mathematics teaching systematic counting of triangles How Many Triangles In Diagram Let s(n) be the number of triangle for n floors: Is there any other way to count the no. In this article provides the simple tricks with formulas to find the number of triangles for the following figures. If it has combination of more than one squares, we have to mark the spot where it joins. Previous video in this. How Many Triangles In Diagram.
From www.mometrix.com
Different Types of Triangles (Video & Practice) How Many Triangles In Diagram How many triangles are there in this diagram? I have manually counted the no of triangles in the diagram. I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. If the given figure has only one square or rectangle, then the formula to find the number of. How Many Triangles In Diagram.
From www.cuemath.com
Triangles Definition, Properties, Formula Triangle Shape How Many Triangles In Diagram How many triangles are there in the figure? Is there any other way to count the no. In this article provides the simple tricks with formulas to find the number of triangles for the following figures. In the following examples you can see it in detail. I have manually counted the no of triangles in the diagram. The star has. How Many Triangles In Diagram.
From thirdspacelearning.com
Types Of Triangles GCSE Maths Steps, Examples & Worksheet How Many Triangles In Diagram How many triangles are there in this diagram? Previous video in this series:. I have manually counted the no of triangles in the diagram. I want to count the number of triangle in the following diagram. Let s(n) be the number of triangle for n floors: If the given figure has only one square or rectangle, then the formula to. How Many Triangles In Diagram.
From www.pinterest.co.uk
Different Types of Triangles with definitions angles infographic How Many Triangles In Diagram If the given figure has only one square or rectangle, then the formula to find the number of triangles is. In this article provides the simple tricks with formulas to find the number of triangles for the following figures. How many triangles are there in the figure? Let s(n) be the number of triangle for n floors: How many triangles. How Many Triangles In Diagram.
From www.fullpotentialtutor.com
Types of Triangles Definitions, Properties, Examples Full Potential How Many Triangles In Diagram I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. The no of triangles is 44. Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): To obtain a recurssion formula for the $t_n$ we have to. How many. How Many Triangles In Diagram.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Owlcation Education How Many Triangles In Diagram If it has combination of more than one squares, we have to mark the spot where it joins. I have manually counted the no of triangles in the diagram. How many triangles are there in the figure? Previous video in this series:. Let s(n) be the number of triangle for n floors: Number of diagonals ⋅ number of blocks. In. How Many Triangles In Diagram.
From www.amathsdictionaryforkids.com
acute triangle A Maths Dictionary for Kids Quick Reference by Jenny How Many Triangles In Diagram In the following examples you can see it in detail. To obtain a recurssion formula for the $t_n$ we have to. The star has $5$ vertices, hence: Let s(n) be the number of triangle for n floors: If it has combination of more than one squares, we have to mark the spot where it joins. I want to count the. How Many Triangles In Diagram.
From howaboutthat.site
How Many Triangles Are There? Can You Solve the Puzzle? How About That? How Many Triangles In Diagram Let s(n) be the number of triangle for n floors: I have manually counted the no of triangles in the diagram. To obtain a recurssion formula for the $t_n$ we have to. Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): In this article provides the simple tricks with formulas to. How Many Triangles In Diagram.
From www.chilimath.com
Classifying Triangles by Angles ChiliMath How Many Triangles In Diagram Is there any other way to count the no. To obtain a recurssion formula for the $t_n$ we have to. Number of diagonals ⋅ number of blocks. The no of triangles is 44. If it has combination of more than one squares, we have to mark the spot where it joins. Let s(n) be the number of triangle for n. How Many Triangles In Diagram.
From brainly.com
How many triangles in the diagram can be mapped to one another by How Many Triangles In Diagram I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): If the given figure has only one square or rectangle, then the formula to find the number of triangles. How Many Triangles In Diagram.
From www.chilimath.com
Classifying Triangles by Sides ChiliMath How Many Triangles In Diagram The no of triangles is 44. Previous video in this series:. I have manually counted the no of triangles in the diagram. In this article provides the simple tricks with formulas to find the number of triangles for the following figures. I want to count the number of triangle in the following diagram. In the following examples you can see. How Many Triangles In Diagram.
From www.chegg.com
Solved STEP 2 Puzzle 2 How many triangles are in the How Many Triangles In Diagram Let s(n) be the number of triangle for n floors: Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): Is there any other way to count the no. The no of triangles is 44. If it has combination of more than one squares, we have to mark the spot where it. How Many Triangles In Diagram.
From www.youtube.com
Can You Determine How Many Triangles are in Each Shape? StepbyStep How Many Triangles In Diagram Previous video in this series:. To obtain a recurssion formula for the $t_n$ we have to. If it has combination of more than one squares, we have to mark the spot where it joins. Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): The star has $5$ vertices, hence: In this. How Many Triangles In Diagram.
From mybrainware.com
How Many Triangles How Many Triangles In Diagram I want to count the number of triangle in the following diagram. The no of triangles is 44. Number of diagonals ⋅ number of blocks. In the following examples you can see it in detail. In this article provides the simple tricks with formulas to find the number of triangles for the following figures. To obtain a recurssion formula for. How Many Triangles In Diagram.
From www.youtube.com
How many triangles are in this figure? Counting the triangles YouTube How Many Triangles In Diagram To obtain a recurssion formula for the $t_n$ we have to. I want to count the number of triangle in the following diagram. Let s(n) be the number of triangle for n floors: Previous video in this series:. In the following examples you can see it in detail. How many triangles are there in the figure? Number of diagonals ⋅. How Many Triangles In Diagram.
From en.wikipedia.org
Triangle Wikipedia How Many Triangles In Diagram In this article provides the simple tricks with formulas to find the number of triangles for the following figures. I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. Is there any other way to count the no. To obtain a recurssion formula for the $t_n$ we. How Many Triangles In Diagram.
From coolmaths.art
Math Puzzles How Many Triangles Maths For Kids How Many Triangles In Diagram Let s(n) be the number of triangle for n floors: I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. Is there any other way to count the no. In the following examples you can see it in detail. The no of triangles is 44. If the. How Many Triangles In Diagram.
From www.youtube.com
How many triangles are there? YouTube How Many Triangles In Diagram I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. In the following examples you can see it in detail. Number of diagonals ⋅ number of blocks. Is there any other way to count the no. I want to count the number of triangle in the following. How Many Triangles In Diagram.
From www.ck12.org
Classifying Polygons CK12 Foundation How Many Triangles In Diagram How many triangles are there in this diagram? To obtain a recurssion formula for the $t_n$ we have to. The star has $5$ vertices, hence: In the following examples you can see it in detail. I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where the floors are added below. The no. How Many Triangles In Diagram.
From www.rd.com
How Many Triangles Do You See? Learn the Answer Reader's Digest How Many Triangles In Diagram The no of triangles is 44. To obtain a recurssion formula for the $t_n$ we have to. Number of diagonals ⋅ number of blocks. Let s(n) be the number of triangle for n floors: In this article provides the simple tricks with formulas to find the number of triangles for the following figures. I want to count the number of. How Many Triangles In Diagram.
From www.youtube.com
Count The Number of Triangles in 5 Pointed Star YouTube How Many Triangles In Diagram To obtain a recurssion formula for the $t_n$ we have to. Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): Previous video in this series:. How many triangles are there in this diagram? If it has combination of more than one squares, we have to mark the spot where it joins.. How Many Triangles In Diagram.
From mathsexplorer.blogspot.ca
Maths Discoveries How Many Triangles in a Triangle? How Many Triangles In Diagram Each vertex of the star can be a vertex of $2$ triangles in one direction (left or right): In the following examples you can see it in detail. How many triangles are there in this diagram? The star has $5$ vertices, hence: I looked by recurrence at how many triangles are added when moving from k to k+1 floors, where. How Many Triangles In Diagram.