Points Of Inflection Sin . The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Consider a function y = f (x), which is continuous at a point x0. Definition of an inflection point. A point of inflection is any point at which a curve changes from being convex to being concave. In this article, the concept and meaning of. Review your knowledge of inflection points and how we use differential calculus to find them. An inflection point is a point on a function where the curvature of the function changes sign. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? This means that a point of inflection is a point where the second derivative changes. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). Stationary points that are not local extrema are. Concave upward is when the slope. The function f (x) can have a finite.
from www.numerade.com
Consider a function y = f (x), which is continuous at a point x0. Concave upward is when the slope. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? In this article, the concept and meaning of. Definition of an inflection point. Review your knowledge of inflection points and how we use differential calculus to find them. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). This means that a point of inflection is a point where the second derivative changes. An inflection point is a point on a function where the curvature of the function changes sign. A point of inflection is any point at which a curve changes from being convex to being concave.
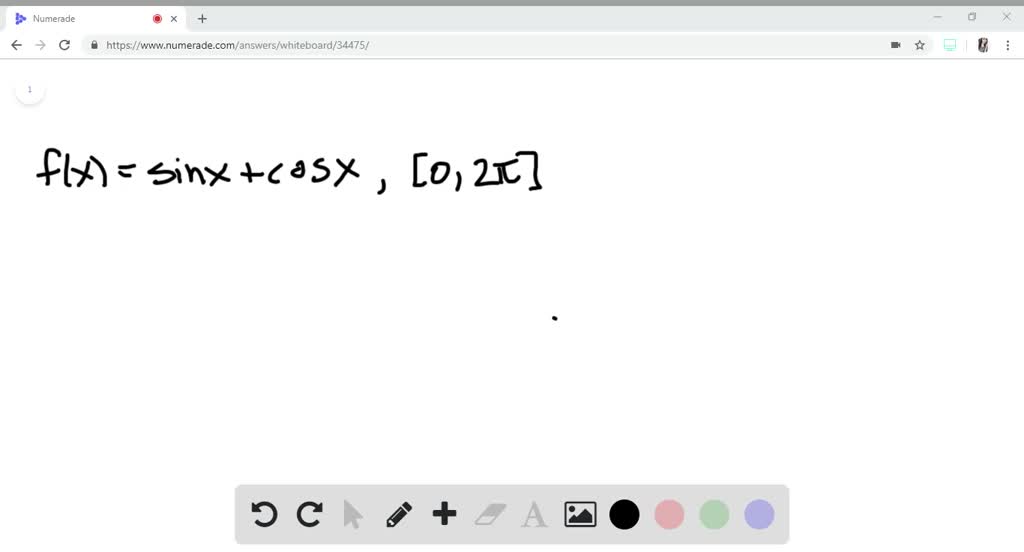
SOLVEDFinding Points of Inflection In Exercises 1732, find the points
Points Of Inflection Sin Consider a function y = f (x), which is continuous at a point x0. An inflection point is a point on a function where the curvature of the function changes sign. The function f (x) can have a finite. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Consider a function y = f (x), which is continuous at a point x0. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). The point where the function is neither concave nor convex is known as inflection point or the point of inflection. This means that a point of inflection is a point where the second derivative changes. Stationary points that are not local extrema are. Review your knowledge of inflection points and how we use differential calculus to find them. Definition of an inflection point. In this article, the concept and meaning of. A point of inflection is any point at which a curve changes from being convex to being concave. Concave upward is when the slope.
From socratic.org
Is f(x)=cosx concave or convex at x=(3pi)/2? Socratic Points Of Inflection Sin A point of inflection is any point at which a curve changes from being convex to being concave. Concave upward is when the slope. Review your knowledge of inflection points and how we use differential calculus to find them. In this article, the concept and meaning of. The point where the function is neither concave nor convex is known as. Points Of Inflection Sin.
From www.chegg.com
Solved Find the points of inflection of the graph of the Points Of Inflection Sin An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Concave upward is when the slope. A point of inflection is any point at which a curve changes from being convex to being concave. Stationary points that are not local extrema are. The point where. Points Of Inflection Sin.
From www.youtube.com
Points of Inflection from f(x)=cos(2x) YouTube Points Of Inflection Sin The function f (x) can have a finite. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Consider a function y = f (x), which is continuous at a point x0. Stationary points that are not local extrema are. A point of inflection is. Points Of Inflection Sin.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection Sin An inflection point is a point on a function where the curvature of the function changes sign. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). Stationary points that are not local extrema are. Consider a function y = f. Points Of Inflection Sin.
From www.hanlin.com
AQA A Level Maths Pure复习笔记7.4.2 Points of Inflection翰林国际教育 Points Of Inflection Sin An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Review your knowledge of inflection points and how we use differential calculus to find them. Stationary points that are not local extrema are. Definition of an inflection point. An inflection point is a point on. Points Of Inflection Sin.
From www.youtube.com
🔶36 Increasing and Decreasing Interval, Relative Extrema, Concavity Points Of Inflection Sin Consider a function y = f (x), which is continuous at a point x0. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. An inflection point is a point on a function where the curvature of the function changes sign. This means that a point of inflection is a. Points Of Inflection Sin.
From mungfali.com
Question Video Finding The 푥coordinates Of The Inflection Points Of A 168 Points Of Inflection Sin In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). In this article, the concept and meaning of. An inflection point is a point on a function where the curvature of the function changes sign. A point of inflection is any. Points Of Inflection Sin.
From collegedunia.com
Inflection Point Calculus, Graph & Concavity Points Of Inflection Sin The function f (x) can have a finite. This means that a point of inflection is a point where the second derivative changes. In this article, the concept and meaning of. Consider a function y = f (x), which is continuous at a point x0. Review your knowledge of inflection points and how we use differential calculus to find them.. Points Of Inflection Sin.
From quizlet.com
**In this exercise, determine the points of inflection and** Quizlet Points Of Inflection Sin In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). Review your knowledge of inflection points and how we use differential calculus to find them. Definition of an inflection point. A point of inflection is any point at which a curve. Points Of Inflection Sin.
From brainly.com
What are the inflection points for the function f ( x ) = sin ( π x − 2 Points Of Inflection Sin An inflection point is a point on a function where the curvature of the function changes sign. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Stationary points that are not local extrema are. A point of inflection is any point at which a. Points Of Inflection Sin.
From www.slideserve.com
PPT Find the inflection points of the following function f ( x ) = 9 Points Of Inflection Sin The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Stationary points that are not local extrema are. The function f (x) can have a finite. An inflection point is a point on a function where the curvature of the function changes sign. In typical problems, we find a function's. Points Of Inflection Sin.
From math.stackexchange.com
calculus Find critical points and inflection points given the Points Of Inflection Sin This means that a point of inflection is a point where the second derivative changes. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable. Points Of Inflection Sin.
From www.gauthmath.com
Solved Suppose (f''=sin (2^x )) for (1 Points Of Inflection Sin Concave upward is when the slope. An inflection point is a point on a function where the curvature of the function changes sign. Stationary points that are not local extrema are. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Definition of an inflection point. Review your knowledge of. Points Of Inflection Sin.
From www.studypool.com
SOLUTION Section 3 5 concavity and points of inflection Studypool Points Of Inflection Sin An inflection point is a point on a function where the curvature of the function changes sign. The function f (x) can have a finite. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). In this article, the concept and. Points Of Inflection Sin.
From dxosthrci.blob.core.windows.net
Point Of Inflection Non Continuous Function at Susie Thomas blog Points Of Inflection Sin The function f (x) can have a finite. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Review your knowledge of inflection points and how we use differential calculus to find them. Concave upward is when the slope. In typical problems, we find a. Points Of Inflection Sin.
From slideplayer.com
Find the inflection points of the following function f ( x ) = 9 x sin Points Of Inflection Sin The function f (x) can have a finite. Stationary points that are not local extrema are. A point of inflection is any point at which a curve changes from being convex to being concave. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Consider a function y = f. Points Of Inflection Sin.
From www.dreamstime.com
Inflection Point on Graph of Function. Stock Vector Illustration of Points Of Inflection Sin Definition of an inflection point. Consider a function y = f (x), which is continuous at a point x0. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? In this article, the concept and meaning of. Review your knowledge of inflection points and how. Points Of Inflection Sin.
From www.youtube.com
Find point of inflection for trig function tan(x) YouTube Points Of Inflection Sin In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). Review your knowledge of inflection points and how we use differential calculus to find them. The function f (x) can have a finite. In this article, the concept and meaning of.. Points Of Inflection Sin.
From math.stackexchange.com
trigonometry How to determine the maximum of a sine graph with only 2 Points Of Inflection Sin An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Definition of an inflection point. A point of inflection is any point at which a curve changes from being convex to being concave. In typical problems, we find a function's inflection point by using \(f''=0\). Points Of Inflection Sin.
From www.coursehero.com
[Solved] State the xcoordinates of the inflection points of the curve Points Of Inflection Sin In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). The function f (x) can have a finite. In this article, the concept and meaning of. Stationary points that are not local extrema are. Consider a function y = f (x),. Points Of Inflection Sin.
From www.shutterstock.com
Inflection Point On Graph Function Vector Stock Vector (Royalty Free Points Of Inflection Sin The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Concave upward is when the slope. Consider a function y = f (x), which is continuous at a point x0. In this article, the concept and meaning of. Review your knowledge of inflection points and how we use differential calculus. Points Of Inflection Sin.
From socratic.org
What are the inflection points for (x^2)/(x^2+1)? Socratic Points Of Inflection Sin Review your knowledge of inflection points and how we use differential calculus to find them. A point of inflection is any point at which a curve changes from being convex to being concave. In this article, the concept and meaning of. Definition of an inflection point. Concave upward is when the slope. Stationary points that are not local extrema are.. Points Of Inflection Sin.
From www.numerade.com
SOLVEDFinding Points of Inflection In Exercises 1732, find the points Points Of Inflection Sin A point of inflection is any point at which a curve changes from being convex to being concave. The function f (x) can have a finite. Consider a function y = f (x), which is continuous at a point x0. An inflection point is a point on a function where the curvature of the function changes sign. Concave upward is. Points Of Inflection Sin.
From www.linstitute.net
IB DP Maths AI HL复习笔记5.2.6 Concavity & Points of Inflection翰林国际教育 Points Of Inflection Sin In this article, the concept and meaning of. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? The function f (x) can have a finite. Consider a function y = f (x), which is continuous at a point x0. A point of inflection is. Points Of Inflection Sin.
From www.radfordmathematics.com
Point of Inflection Calculus Points Of Inflection Sin An inflection point is a point on a function where the curvature of the function changes sign. Concave upward is when the slope. Stationary points that are not local extrema are. A point of inflection is any point at which a curve changes from being convex to being concave. An inflection point is where a curve changes from concave upward. Points Of Inflection Sin.
From mathemerize.com
What is the Point of Inflection ? Mathemerize Points Of Inflection Sin Consider a function y = f (x), which is continuous at a point x0. Definition of an inflection point. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. In this article, the concept and meaning of. Concave upward is when the slope. The function f (x) can have a. Points Of Inflection Sin.
From www.nagwa.com
Question Video Finding the Inflection Points of a Function from the Points Of Inflection Sin Stationary points that are not local extrema are. Review your knowledge of inflection points and how we use differential calculus to find them. The function f (x) can have a finite. This means that a point of inflection is a point where the second derivative changes. An inflection point is a point on a function where the curvature of the. Points Of Inflection Sin.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection Sin Definition of an inflection point. A point of inflection is any point at which a curve changes from being convex to being concave. This means that a point of inflection is a point where the second derivative changes. Concave upward is when the slope. Review your knowledge of inflection points and how we use differential calculus to find them. Stationary. Points Of Inflection Sin.
From mungfali.com
How To Find Inflection Points Of A Function Points Of Inflection Sin The point where the function is neither concave nor convex is known as inflection point or the point of inflection. Consider a function y = f (x), which is continuous at a point x0. Review your knowledge of inflection points and how we use differential calculus to find them. In typical problems, we find a function's inflection point by using. Points Of Inflection Sin.
From www.numerade.com
SOLVED Determine the points of inflection of the function f(x) = x Points Of Inflection Sin Consider a function y = f (x), which is continuous at a point x0. This means that a point of inflection is a point where the second derivative changes. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign of \(f''\). Definition of. Points Of Inflection Sin.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Points Of Inflection Sin Stationary points that are not local extrema are. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Concave upward is when the slope. In this article, the concept and meaning of. This means that a point of inflection is a point where the second. Points Of Inflection Sin.
From www.chegg.com
Solved Find the points of inflection of the graph of the Points Of Inflection Sin An inflection point is a point on a function where the curvature of the function changes sign. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? Definition of an inflection point. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided. Points Of Inflection Sin.
From www.soft-boys.com
Symbolab Inflection Points Points Of Inflection Sin Definition of an inflection point. Consider a function y = f (x), which is continuous at a point x0. An inflection point is where a curve changes from concave upward to concave downward (or vice versa) so what is concave upward / downward ? This means that a point of inflection is a point where the second derivative changes. Stationary. Points Of Inflection Sin.
From www.youtube.com
Find the Intervals where the Function is Concave Up and Down f(x) = 14 Points Of Inflection Sin A point of inflection is any point at which a curve changes from being convex to being concave. Consider a function y = f (x), which is continuous at a point x0. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. An inflection point is where a curve changes. Points Of Inflection Sin.
From www.youtube.com
Find increasing decreasing intervals, min max concavity, inflection Points Of Inflection Sin A point of inflection is any point at which a curve changes from being convex to being concave. Review your knowledge of inflection points and how we use differential calculus to find them. In typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and checking the sign. Points Of Inflection Sin.