Continuous Linear Functional Example . These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Let $x$ be a normed space. Let v be a normed vector space, and let l be a linear functional on v. If a function is not continuous at x0, we say it is discontinuous at x0. Numerous examples of linear continuous functionals are provided and their. In this chapter we address the following subjects: A function f is continuous at a point x0 if. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. Lim f(x) = f(x0) x→x0. The connection between real and complex functionals; Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. We consider the notions of linear, continuous and bounded functional. Then the following four statements are equivalent:. Learn about the dual spaces, bounded linear operators, and riesz representation theorems for normed linear spaces and compact metric.
from www.media4math.com
The connection between real and complex functionals; Let v be a normed vector space, and let l be a linear functional on v. In this chapter we address the following subjects: Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. A function f is continuous at a point x0 if. Numerous examples of linear continuous functionals are provided and their. Let $x$ be a normed space. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Learn about the dual spaces, bounded linear operators, and riesz representation theorems for normed linear spaces and compact metric. Lim f(x) = f(x0) x→x0.
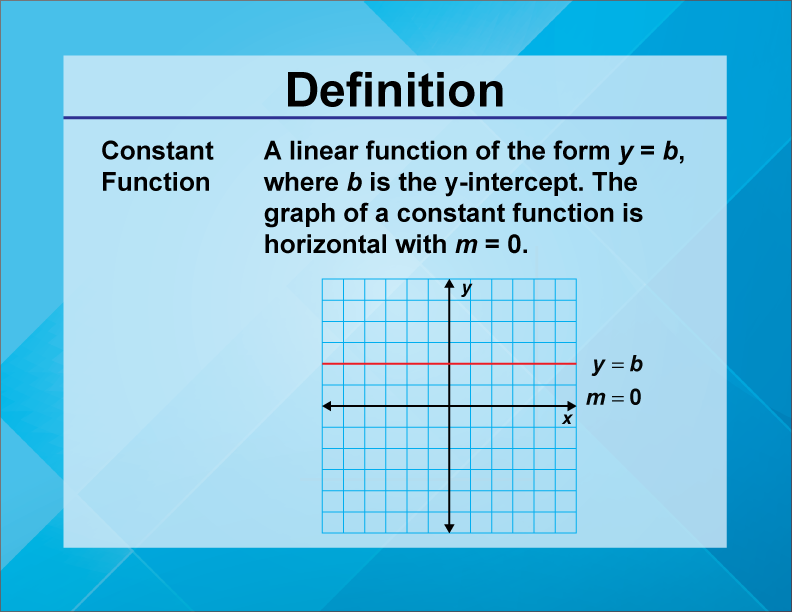
Function ConceptsConstant Function Media4Math
Continuous Linear Functional Example Let $x$ be a normed space. The connection between real and complex functionals; Then the following four statements are equivalent:. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. Numerous examples of linear continuous functionals are provided and their. If a function is not continuous at x0, we say it is discontinuous at x0. In this chapter we address the following subjects: Learn about the dual spaces, bounded linear operators, and riesz representation theorems for normed linear spaces and compact metric. Lim f(x) = f(x0) x→x0. A function f is continuous at a point x0 if. We consider the notions of linear, continuous and bounded functional. Let $x$ be a normed space. Let v be a normed vector space, and let l be a linear functional on v. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$.
From www.youtube.com
Constant and Linear Functions 1 2 YouTube Continuous Linear Functional Example A function f is continuous at a point x0 if. Numerous examples of linear continuous functionals are provided and their. Lim f(x) = f(x0) x→x0. Let v be a normed vector space, and let l be a linear functional on v. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $. Continuous Linear Functional Example.
From www.youtube.com
Reading Graph of a Linear Function to Find Two Function Values f(5) & f Continuous Linear Functional Example A function f is continuous at a point x0 if. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Let $x$ be a normed space. In this chapter we address the following subjects: Learn about the dual spaces, bounded linear operators, and riesz representation theorems for normed linear spaces and. Continuous Linear Functional Example.
From www.expii.com
Continuous Data Definition & Examples Expii Continuous Linear Functional Example Let v be a normed vector space, and let l be a linear functional on v. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. A function f is continuous at a point x0 if. If a function is not continuous at x0, we say it is discontinuous at x0. Lim. Continuous Linear Functional Example.
From www.slideserve.com
PPT Linear Constantcoefficient Difference Equations PowerPoint Continuous Linear Functional Example Lim f(x) = f(x0) x→x0. A function f is continuous at a point x0 if. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. If a function is not continuous at x0, we say it is discontinuous at x0. Then the following four statements are equivalent:. Prove that a linear. Continuous Linear Functional Example.
From hxeitgxri.blob.core.windows.net
Continuous Linear Functional Space at Melissa Carlisle blog Continuous Linear Functional Example Let v be a normed vector space, and let l be a linear functional on v. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Then the. Continuous Linear Functional Example.
From www.media4math.com
Graphs of Linear Functions Media4Math Continuous Linear Functional Example Lim f(x) = f(x0) x→x0. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. Let v be a normed vector space, and let l be a linear functional on v. We consider the notions of linear, continuous and bounded functional. Then the following four statements are equivalent:. Learn about the dual. Continuous Linear Functional Example.
From pathshalanepal.com
What is a constant linear function? Continuous Linear Functional Example Let v be a normed vector space, and let l be a linear functional on v. We consider the notions of linear, continuous and bounded functional. In this chapter we address the following subjects: These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Numerous examples of linear continuous functionals are. Continuous Linear Functional Example.
From www.ncl.ac.uk
Numeracy, Maths and Statistics Academic Skills Kit Continuous Linear Functional Example If a function is not continuous at x0, we say it is discontinuous at x0. Let v be a normed vector space, and let l be a linear functional on v. We consider the notions of linear, continuous and bounded functional. A function f is continuous at a point x0 if. The connection between real and complex functionals; These notes. Continuous Linear Functional Example.
From granthamvanderch.blogspot.com
Example of Continuous Function That is Not Differentiable Grantham Continuous Linear Functional Example Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. We consider the notions of linear, continuous and bounded functional. If a function is not continuous at x0, we say it is discontinuous at x0. These notes cover the basics of normed and banach spaces, the lebesgue. Continuous Linear Functional Example.
From saylordotorg.github.io
Graphing the Basic Functions Continuous Linear Functional Example These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. The connection between real and complex functionals; Lim f(x) = f(x0) x→x0. A function f is continuous at a point x0 if. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $. Continuous Linear Functional Example.
From educational.my.id
Linear And Functions Worksheet Educational.my.id Continuous Linear Functional Example The connection between real and complex functionals; Numerous examples of linear continuous functionals are provided and their. We consider the notions of linear, continuous and bounded functional. Let v be a normed vector space, and let l be a linear functional on v. A function f is continuous at a point x0 if. Prove that a linear functional $f:x \to. Continuous Linear Functional Example.
From exomdjudt.blob.core.windows.net
Continuous Linear Functional Definition at Vilma Vinson blog Continuous Linear Functional Example Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. If a function is not continuous at x0, we say it is discontinuous at x0. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. A linear functional. Continuous Linear Functional Example.
From www.media4math.com
Function ConceptsConstant Function Media4Math Continuous Linear Functional Example Numerous examples of linear continuous functionals are provided and their. A function f is continuous at a point x0 if. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Let $x$ be a normed space. Then the following four statements are equivalent:. Prove that a linear functional $f:x \to \mathbb{r}$. Continuous Linear Functional Example.
From machinelearningmastery.com
A Gentle Introduction to Continuous Functions Continuous Linear Functional Example A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. Let $x$ be a normed space. Lim f(x) = f(x0) x→x0. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. Learn about the dual spaces, bounded linear operators,. Continuous Linear Functional Example.
From brainly.ph
Identify the quadratic term, linear term, and constant of each Continuous Linear Functional Example Let v be a normed vector space, and let l be a linear functional on v. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. The connection between real and complex functionals; We consider the notions of linear, continuous and bounded functional. A function f is. Continuous Linear Functional Example.
From www.pinterest.com
Determine if a function is discrete or continuous by analyzing the Continuous Linear Functional Example The connection between real and complex functionals; A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. If a function is not continuous at x0, we say it is discontinuous at x0. Let. Continuous Linear Functional Example.
From galesdevescithhen.blogspot.com
Describe Limits of a Function Help Us Defne Continuity of a Funtion at Continuous Linear Functional Example Let $x$ be a normed space. Numerous examples of linear continuous functionals are provided and their. We consider the notions of linear, continuous and bounded functional. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. The connection between real and complex functionals; Then the following four statements are equivalent:. In this. Continuous Linear Functional Example.
From www.factorworksheets.com
Factoring All Types Of Polynomials Worksheet Continuous Linear Functional Example Learn about the dual spaces, bounded linear operators, and riesz representation theorems for normed linear spaces and compact metric. Numerous examples of linear continuous functionals are provided and their. A function f is continuous at a point x0 if. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. Let v be. Continuous Linear Functional Example.
From hxeitgxri.blob.core.windows.net
Continuous Linear Functional Space at Melissa Carlisle blog Continuous Linear Functional Example These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. If a function is not continuous at x0, we say it is discontinuous at x0. We consider the. Continuous Linear Functional Example.
From www.pinterest.com
Pin by Jenny Borovsky on Teaching Algebra Topics Linear function Continuous Linear Functional Example A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. A function f is continuous at a point x0 if. Lim f(x) = f(x0) x→x0. We consider the notions of linear, continuous and bounded functional. The connection between real and complex functionals; Let $x$ be a normed space. Prove that a linear. Continuous Linear Functional Example.
From kirbyaborted1970.blogspot.com
Can a Linear Function Be Continuous but Not Have a Domain and Range of Continuous Linear Functional Example We consider the notions of linear, continuous and bounded functional. Then the following four statements are equivalent:. If a function is not continuous at x0, we say it is discontinuous at x0. Let $x$ be a normed space. Lim f(x) = f(x0) x→x0. The connection between real and complex functionals; Learn about the dual spaces, bounded linear operators, and riesz. Continuous Linear Functional Example.
From ortizhihsmath.weebly.com
Math 1 Continuous Linear Functional Example Let v be a normed vector space, and let l be a linear functional on v. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. In this chapter we address the following subjects: Lim f(x) = f(x0) x→x0. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only. Continuous Linear Functional Example.
From www.slideshare.net
Linear differential equation with constant coefficient Continuous Linear Functional Example We consider the notions of linear, continuous and bounded functional. The connection between real and complex functionals; Then the following four statements are equivalent:. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. A linear functional is a mapping from a vector space to its base. Continuous Linear Functional Example.
From www.youtube.com
How to Representing a Constant Function YouTube Continuous Linear Functional Example We consider the notions of linear, continuous and bounded functional. A function f is continuous at a point x0 if. Numerous examples of linear continuous functionals are provided and their. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. In this chapter we address the following subjects: These notes cover the. Continuous Linear Functional Example.
From www.youtube.com
L11.3 A Linear Function of a Continuous Random Variable YouTube Continuous Linear Functional Example Lim f(x) = f(x0) x→x0. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. Let $x$ be a normed space. A function f is continuous at a point x0 if. The connection between real and complex functionals; These notes cover the basics of normed and banach. Continuous Linear Functional Example.
From www.cuemath.com
Constant Function Definition Graphs Examples Cuemath Continuous Linear Functional Example We consider the notions of linear, continuous and bounded functional. Let $x$ be a normed space. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. A function f is continuous at a point x0 if. A linear functional is a mapping from a vector space to. Continuous Linear Functional Example.
From www.youtube.com
Alg2T Ch1.1.2 One to One, Continuous, Linear Functions YouTube Continuous Linear Functional Example A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Lim f(x) = f(x0) x→x0. We consider the notions of linear, continuous and bounded functional. A function f is continuous at a point. Continuous Linear Functional Example.
From www.cuemath.com
Constant Function Definition Graphs Examples Cuemath Continuous Linear Functional Example Then the following four statements are equivalent:. A function f is continuous at a point x0 if. In this chapter we address the following subjects: We consider the notions of linear, continuous and bounded functional. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. The connection. Continuous Linear Functional Example.
From www.youtube.com
Graphs of Functions Constant, Linear, Quadratic, Cubic YouTube Continuous Linear Functional Example Learn about the dual spaces, bounded linear operators, and riesz representation theorems for normed linear spaces and compact metric. In this chapter we address the following subjects: Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. A linear functional is a mapping from a vector space. Continuous Linear Functional Example.
From www.cuemath.com
What is Linear Function? Equation, Graph, Definition Continuous Linear Functional Example Lim f(x) = f(x0) x→x0. The connection between real and complex functionals; If a function is not continuous at x0, we say it is discontinuous at x0. In this chapter we address the following subjects: These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. Prove that a linear functional $f:x. Continuous Linear Functional Example.
From www.cuemath.com
Linear Function Formula Learn the Formula of Linear Function Continuous Linear Functional Example We consider the notions of linear, continuous and bounded functional. Lim f(x) = f(x0) x→x0. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if there is a number $ c \in {0, \infty}$. If a function is not continuous at x0, we say it is discontinuous at x0. Then the following four statements are equivalent:.. Continuous Linear Functional Example.
From www.cuemath.com
Constant Function Definition, Graph, Characteristics, Examples Continuous Linear Functional Example Let v be a normed vector space, and let l be a linear functional on v. In this chapter we address the following subjects: If a function is not continuous at x0, we say it is discontinuous at x0. Then the following four statements are equivalent:. Prove that a linear functional $f:x \to \mathbb{r}$ is continuous if and only if. Continuous Linear Functional Example.
From www.youtube.com
linear functions increasing, decreasing, constant YouTube Continuous Linear Functional Example Learn about the dual spaces, bounded linear operators, and riesz representation theorems for normed linear spaces and compact metric. Then the following four statements are equivalent:. A linear functional is a mapping from a vector space to its base field that satisfies linearity conditions. Lim f(x) = f(x0) x→x0. If a function is not continuous at x0, we say it. Continuous Linear Functional Example.
From www.youtube.com
continuous linear functional s YouTube Continuous Linear Functional Example In this chapter we address the following subjects: A function f is continuous at a point x0 if. We consider the notions of linear, continuous and bounded functional. If a function is not continuous at x0, we say it is discontinuous at x0. Let v be a normed vector space, and let l be a linear functional on v. Lim. Continuous Linear Functional Example.
From flamath.com
Linear Function Definition, Graph and Examples Continuous Linear Functional Example If a function is not continuous at x0, we say it is discontinuous at x0. These notes cover the basics of normed and banach spaces, the lebesgue integral, hilbert spaces, and applications to differential. In this chapter we address the following subjects: We consider the notions of linear, continuous and bounded functional. Lim f(x) = f(x0) x→x0. Let $x$ be. Continuous Linear Functional Example.