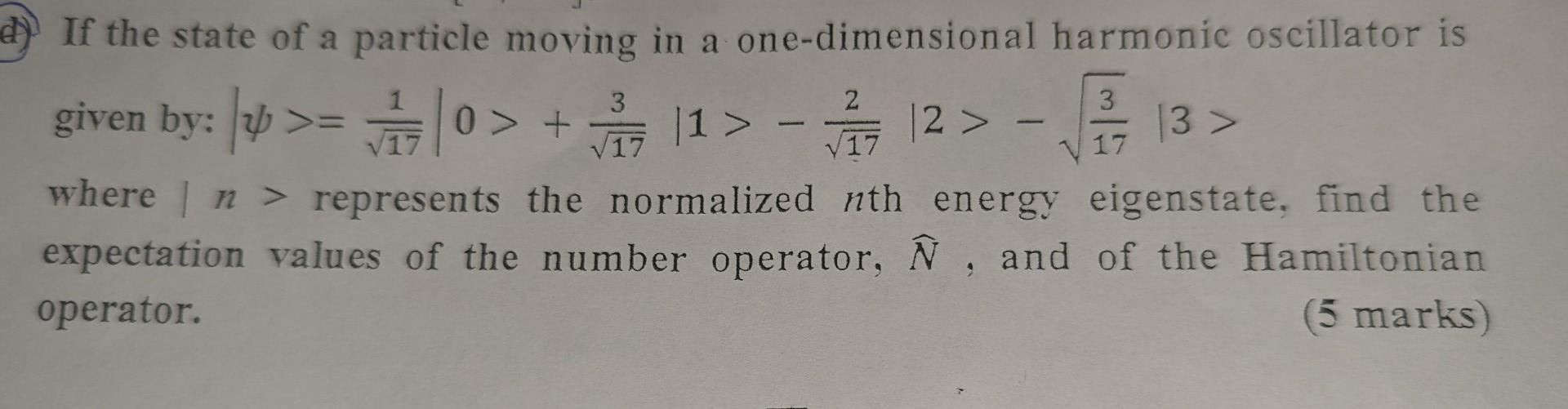Harmonic Oscillator Number Operator . Here is the notation which will be. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. They are two observables (p,x) with the commutation. In previous chapters, we used. 2 reminds us of the difference of two squares of numbers Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. We can define the operators associated with position and momentum.
from www.chegg.com
We can define the operators associated with position and momentum. They are two observables (p,x) with the commutation. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Here is the notation which will be. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. 2 reminds us of the difference of two squares of numbers In previous chapters, we used.
Solved If the state of a particle moving in a
Harmonic Oscillator Number Operator They are two observables (p,x) with the commutation. We can define the operators associated with position and momentum. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. 2 reminds us of the difference of two squares of numbers It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. They are two observables (p,x) with the commutation. In previous chapters, we used. Here is the notation which will be.
From www.cantorsparadise.com
The Quantum Harmonic Oscillator Dirac's Approach by Dan Jackson Harmonic Oscillator Number Operator It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. In previous chapters, we used. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. We can define the operators associated with position and momentum. 2 reminds us of the difference of two squares of numbers They are two. Harmonic Oscillator Number Operator.
From www.youtube.com
Solving the Quantum Harmonic Oscillator using the Algebraic Method Harmonic Oscillator Number Operator Here is the notation which will be. They are two observables (p,x) with the commutation. We can define the operators associated with position and momentum. 2 reminds us of the difference of two squares of numbers In previous chapters, we used. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Since the number operator is exactly. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT Quantum Harmonic Oscillator PowerPoint Presentation, free Harmonic Oscillator Number Operator It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. They are two observables (p,x) with the commutation. We can define the operators associated with position and momentum. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. In previous chapters, we used. Here is the notation which will. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT Quantum Harmonic Oscillator PowerPoint Presentation, free Harmonic Oscillator Number Operator Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. They are two observables (p,x) with the commutation. Here is the notation which will be. 2 reminds us of the difference of two squares of numbers In previous chapters,. Harmonic Oscillator Number Operator.
From www.youtube.com
What is the Number Operator? Harmonic Oscillator Quantum Mechanics Harmonic Oscillator Number Operator Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. In previous chapters, we used. Here is the notation which will be. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. We can define the operators associated with position and momentum. They are two observables (p,x) with the. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT Quantum Harmonic Oscillator PowerPoint Presentation, free Harmonic Oscillator Number Operator They are two observables (p,x) with the commutation. We can define the operators associated with position and momentum. Here is the notation which will be. 2 reminds us of the difference of two squares of numbers It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Since the number operator is exactly the hamiltonian up to some. Harmonic Oscillator Number Operator.
From scoop.eduncle.com
Exercise 4.14 if the state of a particle moving in a onedimensional Harmonic Oscillator Number Operator 2 reminds us of the difference of two squares of numbers They are two observables (p,x) with the commutation. Here is the notation which will be. In previous chapters, we used. We can define the operators associated with position and momentum. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Since the number operator is exactly. Harmonic Oscillator Number Operator.
From www.youtube.com
The Quantum Harmonic Oscillator Part 1 The Classical Harmonic Harmonic Oscillator Number Operator It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. They are two observables (p,x) with the commutation. 2 reminds us of the difference of two squares of numbers We can define the operators associated with position and momentum. Here is the notation which will be. In previous chapters, we used. Since the number operator is exactly. Harmonic Oscillator Number Operator.
From www.chegg.com
Solved The creation and annihilation operators for quantum Harmonic Oscillator Number Operator In previous chapters, we used. Here is the notation which will be. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. We can define the operators associated with position and momentum. 2 reminds us of the difference of. Harmonic Oscillator Number Operator.
From www.chegg.com
Solved 11. LADDER OPERATORS FOR THE HARMONIC OSCILLATOR Harmonic Oscillator Number Operator They are two observables (p,x) with the commutation. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. In previous chapters, we used. Here is the notation which will be. We can define the operators associated with position and momentum. 2 reminds us of the difference of two squares of numbers It. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT 5. The Harmonic Oscillator PowerPoint Presentation, free download Harmonic Oscillator Number Operator Here is the notation which will be. They are two observables (p,x) with the commutation. In previous chapters, we used. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. 2 reminds us of the difference of two squares of numbers It is convenient to introduce dimensionless quantities when discussing the quantum. Harmonic Oscillator Number Operator.
From www.chegg.com
Solved Quantum harmonic oscillator, ladder operator Harmonic Oscillator Number Operator Here is the notation which will be. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. In previous chapters, we used. We can define the operators associated with position and momentum. They are two observables (p,x) with the commutation. 2 reminds us of the difference of two squares of numbers Since the number operator is exactly. Harmonic Oscillator Number Operator.
From www.chegg.com
Solved For the harmonic oscillator, the raising operator Harmonic Oscillator Number Operator It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Here is the notation which will be. They are two observables (p,x) with the commutation. 2 reminds us of the difference of two squares of numbers We can define the operators associated with position and momentum. In previous chapters, we used. Since the number operator is exactly. Harmonic Oscillator Number Operator.
From www.numerade.com
SOLVED The quantum harmonic oscillator Hamiltonian can be written as Harmonic Oscillator Number Operator We can define the operators associated with position and momentum. They are two observables (p,x) with the commutation. Here is the notation which will be. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. In previous chapters, we. Harmonic Oscillator Number Operator.
From www.numerade.com
SOLVED Hamiltonian operator for simple harmonic oscillator is A = p² Harmonic Oscillator Number Operator Here is the notation which will be. In previous chapters, we used. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. They are two observables (p,x) with the commutation. We can define the operators associated with position and. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT Review Three Pictures of Quantum Mechanics PowerPoint Harmonic Oscillator Number Operator In previous chapters, we used. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. We can define the operators associated with position and momentum. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. Here is the notation which will be. They are two observables (p,x) with the. Harmonic Oscillator Number Operator.
From www.youtube.com
Ladder and number operators of the quantum harmonic oscillator YouTube Harmonic Oscillator Number Operator Here is the notation which will be. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. They are two observables (p,x) with the commutation. In previous chapters, we used. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. 2 reminds us of the difference of two squares. Harmonic Oscillator Number Operator.
From www.youtube.com
Harmonic Oscillator By Operator Method Quantum Mechanics M.Sc Harmonic Oscillator Number Operator Here is the notation which will be. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. They are two observables (p,x) with the commutation. We can define the operators associated with position and momentum. In previous chapters, we used. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously. Harmonic Oscillator Number Operator.
From www.youtube.com
Ladder Operators in Quantum Harmonic Oscillator; Uncertainty Relation Harmonic Oscillator Number Operator Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. In previous chapters, we used. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Here is the notation which will be. We can define the operators associated with position and momentum. They are two observables (p,x) with the. Harmonic Oscillator Number Operator.
From www.youtube.com
OPERATOR FORMULATION OF HARMONIC OSCILLATOR LOWERING AND RISING Harmonic Oscillator Number Operator Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. Here is the notation which will be. We can define the operators associated with position and momentum. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. 2 reminds us of the difference of two squares of numbers They. Harmonic Oscillator Number Operator.
From www.numerade.com
SOLVED Title Quantum Mechanics 2D Harmonic Oscillator and Identical Harmonic Oscillator Number Operator In previous chapters, we used. 2 reminds us of the difference of two squares of numbers It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. They are two observables (p,x) with the commutation. We can define the operators. Harmonic Oscillator Number Operator.
From www.youtube.com
Commutator of Number Operator with Ladder Operators (Quantum Harmonic Harmonic Oscillator Number Operator They are two observables (p,x) with the commutation. 2 reminds us of the difference of two squares of numbers It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. In previous chapters, we used. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. Here is the notation which. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT Harmonic oscillator and coherent states PowerPoint Presentation Harmonic Oscillator Number Operator In previous chapters, we used. We can define the operators associated with position and momentum. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Here is the notation which will be. 2 reminds us of the difference of two squares of numbers They are two observables (p,x) with the commutation. Since the number operator is exactly. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT Quantum Harmonic Oscillator PowerPoint Presentation, free Harmonic Oscillator Number Operator It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Here is the notation which will be. In previous chapters, we used. We can define the operators associated with position and momentum. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. 2 reminds us of the difference of. Harmonic Oscillator Number Operator.
From www.youtube.com
Solving the quantum harmonic oscillator with ladder operators YouTube Harmonic Oscillator Number Operator They are two observables (p,x) with the commutation. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. In previous chapters, we used. 2 reminds us of the difference of two squares of numbers Here is the notation which will be. Since the number operator is exactly the hamiltonian up to some constants, the two operators are. Harmonic Oscillator Number Operator.
From www.youtube.com
Quantum Harmonic Oscillator Hamiltonian in terms of Number Operator and Harmonic Oscillator Number Operator Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. In previous chapters, we used. They are two observables (p,x) with the commutation. We can define the operators associated with position and momentum. Here is the notation which will be. 2 reminds us of the difference of two squares of numbers It. Harmonic Oscillator Number Operator.
From www.youtube.com
Quantum harmonic oscillator via ladder operators YouTube Harmonic Oscillator Number Operator 2 reminds us of the difference of two squares of numbers Here is the notation which will be. We can define the operators associated with position and momentum. In previous chapters, we used. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. It is convenient to introduce dimensionless quantities when discussing. Harmonic Oscillator Number Operator.
From www.slideserve.com
PPT 5. The Harmonic Oscillator PowerPoint Presentation, free download Harmonic Oscillator Number Operator Here is the notation which will be. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. They are two observables (p,x) with the commutation. 2 reminds us of the difference of two squares of numbers It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. We can define. Harmonic Oscillator Number Operator.
From www.chegg.com
Solved Question 3 The Hamiltonian operator for the Harmonic Oscillator Number Operator We can define the operators associated with position and momentum. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. They are two observables (p,x) with the commutation. In previous chapters, we used. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. 2 reminds us of the difference. Harmonic Oscillator Number Operator.
From www.youtube.com
Aug28 Physics 151 harmonic oscillator, creation and annihilation Harmonic Oscillator Number Operator Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. Here is the notation which will be. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. 2 reminds us of the difference of two squares of numbers They are two observables (p,x) with the commutation. We can define. Harmonic Oscillator Number Operator.
From slideplayer.com
PHY 752 Solid State Physics ppt download Harmonic Oscillator Number Operator In previous chapters, we used. They are two observables (p,x) with the commutation. We can define the operators associated with position and momentum. Here is the notation which will be. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. 2 reminds us of the difference of two squares of numbers Since the number operator is exactly. Harmonic Oscillator Number Operator.
From www.numerade.com
SOLVED B.2 Consider the following state of a harmonic oscillator at t Harmonic Oscillator Number Operator They are two observables (p,x) with the commutation. 2 reminds us of the difference of two squares of numbers It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. Here is the notation which will be. We can define the operators associated with position and momentum. Since the number operator is exactly the hamiltonian up to some. Harmonic Oscillator Number Operator.
From www.chegg.com
Solved If the state of a particle moving in a Harmonic Oscillator Number Operator We can define the operators associated with position and momentum. In previous chapters, we used. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. Here is the notation which will be. They are two observables (p,x) with the commutation. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic. Harmonic Oscillator Number Operator.
From www.youtube.com
06operator method linear harmonic oscillator YouTube Harmonic Oscillator Number Operator Here is the notation which will be. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. In previous chapters, we used. They are two observables (p,x) with the commutation. We can define the operators associated with position and. Harmonic Oscillator Number Operator.
From www.youtube.com
Heisenberg Uncertainty in the Harmonic Oscillator Ground State YouTube Harmonic Oscillator Number Operator They are two observables (p,x) with the commutation. It is convenient to introduce dimensionless quantities when discussing the quantum harmonic oscillator. We can define the operators associated with position and momentum. Since the number operator is exactly the hamiltonian up to some constants, the two operators are simultaneously diagonalizable. 2 reminds us of the difference of two squares of numbers. Harmonic Oscillator Number Operator.