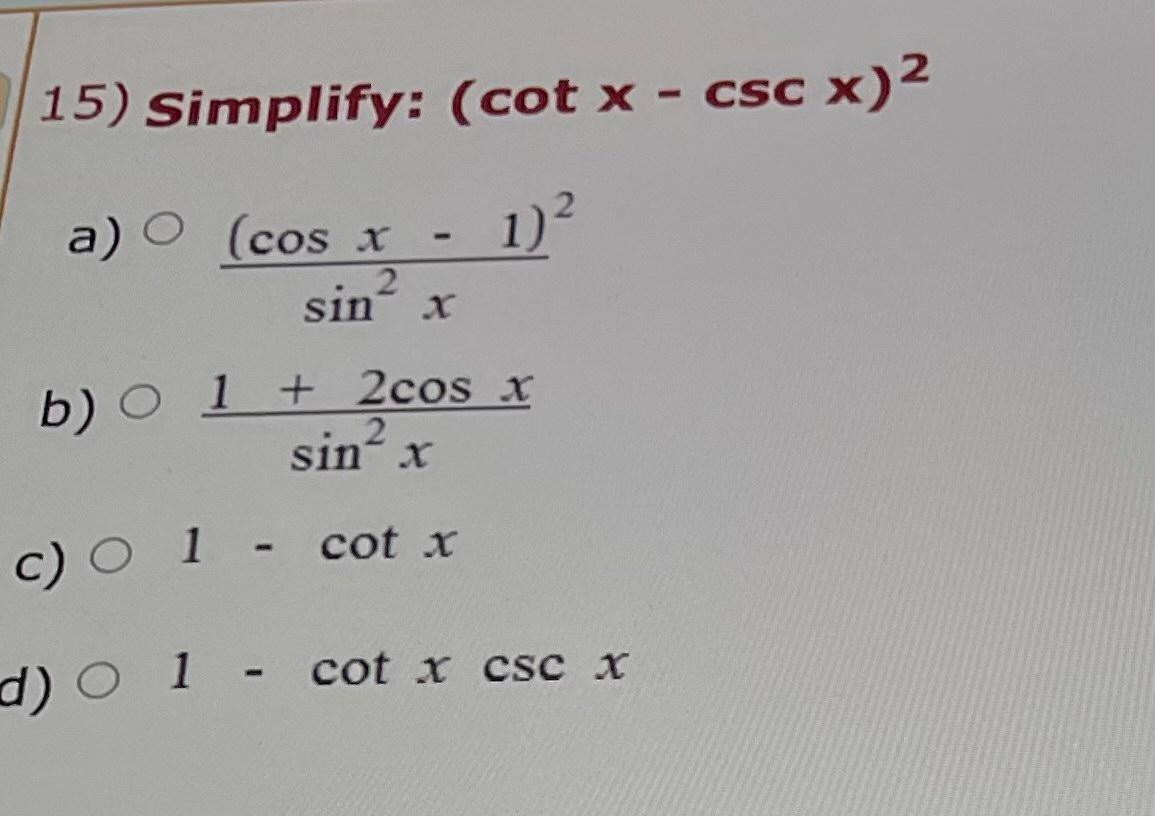Cot 2 X Csc X 5 . We can also divide the other way. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. To find the second solution, subtract the reference angle from π π to find. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. The cosecant function is positive in the first and second quadrants. For example, 1 + cot^2x =. In this section, we will understand the cot^2x identity in trigonometry.
from www.chegg.com
We can also divide the other way. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. For example, 1 + cot^2x =. The cosecant function is positive in the first and second quadrants. In this section, we will understand the cot^2x identity in trigonometry. To find the second solution, subtract the reference angle from π π to find. We have different formulas and identities in trigonometry that involve cot^2x.
Solved Express tan x + cot x in terms of sec x and csc
Cot 2 X Csc X 5 We can also divide the other way. The cosecant function is positive in the first and second quadrants. We can also divide the other way. To find the second solution, subtract the reference angle from π π to find. In this section, we will understand the cot^2x identity in trigonometry. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. For example, 1 + cot^2x =. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We have different formulas and identities in trigonometry that involve cot^2x.
From www.youtube.com
sen x/cos x + tan x/cot x + sec x/csc x=2cot x+1/cot2 x YouTube Cot 2 X Csc X 5 Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the reference angle from π π to find. For example, 1 + cot^2x =. In this section, we will understand the cot^2x identity in trigonometry. The cosecant function is positive in the first and second quadrants. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity.. Cot 2 X Csc X 5.
From www.toppr.com
int e^{x} (cot , x cosec^2 x)dx Cot 2 X Csc X 5 In this section, we will understand the cot^2x identity in trigonometry. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We have different formulas and identities in trigonometry that involve cot^2x. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We can also divide the other way. For example, 1 + cot^2x =. The cosecant function is positive in the. Cot 2 X Csc X 5.
From www.teachoo.com
Ex 5.2, 7 Differentiate 2 root cot (x^2) Teachoo Ex 5.2 Cot 2 X Csc X 5 We can also divide the other way. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the reference angle from π π to find. For example, 1 + cot^2x =. In this section, we will understand the cot^2x identity in trigonometry. The cosecant function is. Cot 2 X Csc X 5.
From www.teachoo.com
Example 3 (ii) Find the integral ∫ cosec x (cosec x + cot x) dx Cot 2 X Csc X 5 To find the second solution, subtract the reference angle from π π to find. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. For example, 1 + cot^2x =. The cosecant function is positive in the first and second quadrants.. Cot 2 X Csc X 5.
From brainly.com
csc^2 (x) 2csc(x) * cot(x) + cot^2 (x) = tan^2 (x/2) simplify Cot 2 X Csc X 5 The cosecant function is positive in the first and second quadrants. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the reference angle from π π to find. For example, 1 + cot^2x =. We have different formulas and identities in trigonometry that involve cot^2x.. Cot 2 X Csc X 5.
From www.toppr.com
tan x + cot x = 2 cosec 2x Cot 2 X Csc X 5 We can also divide the other way. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. For example, 1 + cot^2x =. To find the second solution, subtract the reference angle from π π to find. The cosecant function is positive in the first and second quadrants. In this section, we. Cot 2 X Csc X 5.
From www.toppr.com
"5. 2 cosec ( 2 x + ) cosec ( x = )n(a) ( csc x cdot cot left( frac { x Cot 2 X Csc X 5 In this section, we will understand the cot^2x identity in trigonometry. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We can also divide the other way. To find the second solution, subtract the reference angle from π π to find. The cosecant function is positive in the first and second quadrants. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric. Cot 2 X Csc X 5.
From www.toppr.com
Evaluate displaystyle int frac { cot x}{( cosec x cot x)} dx Cot 2 X Csc X 5 The cosecant function is positive in the first and second quadrants. In this section, we will understand the cot^2x identity in trigonometry. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We have different formulas and identities in trigonometry that involve cot^2x. We can also divide the other way. To find the second solution, subtract the reference angle from π π to find. For. Cot 2 X Csc X 5.
From www.youtube.com
Prove that Cosecx Cotx = Tan(x/2) mathsvideotech YouTube Cot 2 X Csc X 5 We have different formulas and identities in trigonometry that involve cot^2x. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. For example, 1 + cot^2x =. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. In this section, we will understand the cot^2x identity in trigonometry. To find the second solution, subtract the reference angle from π π to find.. Cot 2 X Csc X 5.
From www.gauthmath.com
Solved Find dy/dx . y=5(csc x+cot x)(csc xcot x) dy/dx = [Calculus] Cot 2 X Csc X 5 To find the second solution, subtract the reference angle from π π to find. In this section, we will understand the cot^2x identity in trigonometry. For example, 1 + cot^2x =. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. The cosecant function is positive. Cot 2 X Csc X 5.
From www.numerade.com
SOLVED For the following exercises, simplify the first trigonometric Cot 2 X Csc X 5 To find the second solution, subtract the reference angle from π π to find. We can also divide the other way. For example, 1 + cot^2x =. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. In this section, we will understand the cot^2x identity in trigonometry. The cosecant function is. Cot 2 X Csc X 5.
From aapkatutorclass11and12.blogspot.com
find the possible value of cos x if cot x + cosec x =5 Cot 2 X Csc X 5 To find the second solution, subtract the reference angle from π π to find. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We can also divide the other way. In this section, we will understand the cot^2x identity in trigonometry. For example, 1 +. Cot 2 X Csc X 5.
From www.coursehero.com
[Solved] Question 11 (5 points) Simplify cot x csc x cos X. O cot X Cot 2 X Csc X 5 In this section, we will understand the cot^2x identity in trigonometry. For example, 1 + cot^2x =. The cosecant function is positive in the first and second quadrants. We have different formulas and identities in trigonometry that involve cot^2x. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We can also divide the other way. Tan (θ) = sin (θ) cos (θ) that is. Cot 2 X Csc X 5.
From www.toppr.com
mathbf { i } mathbf { } ) ) cosec ( x d x = log csc x cot x + C Cot 2 X Csc X 5 To find the second solution, subtract the reference angle from π π to find. We can also divide the other way. The cosecant function is positive in the first and second quadrants. We have different formulas and identities in trigonometry that involve cot^2x. In this section, we will understand the cot^2x identity in trigonometry. For example, 1 + cot^2x =.. Cot 2 X Csc X 5.
From www.epsilonify.com
Prove that 1 + cot^2(x) = csc^2(x) Epsilonify Cot 2 X Csc X 5 For example, 1 + cot^2x =. We have different formulas and identities in trigonometry that involve cot^2x. In this section, we will understand the cot^2x identity in trigonometry. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the reference angle from π π to find. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity.. Cot 2 X Csc X 5.
From www.youtube.com
Verifying a Trigonometric Identity cot(x)/csc(x) = cos(x) YouTube Cot 2 X Csc X 5 To find the second solution, subtract the reference angle from π π to find. The cosecant function is positive in the first and second quadrants. We can also divide the other way. For example, 1 + cot^2x =. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. In this section, we will understand the cot^2x identity in trigonometry. We have different formulas and identities. Cot 2 X Csc X 5.
From www.chegg.com
Solved Express tan x + cot x in terms of sec x and csc Cot 2 X Csc X 5 We can also divide the other way. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. For example, 1 + cot^2x =. The cosecant function is positive in the first and second quadrants. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. In this section, we will understand the. Cot 2 X Csc X 5.
From www.toppr.com
Evaluateint { cfrac { cosec ^{ 2 }{ x } }{ (1cot ^{ 2 }{ x } ) } dx } Cot 2 X Csc X 5 We have different formulas and identities in trigonometry that involve cot^2x. In this section, we will understand the cot^2x identity in trigonometry. The cosecant function is positive in the first and second quadrants. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the reference angle from π π to find. For example, 1 + cot^2x =. Tan (θ). Cot 2 X Csc X 5.
From www.youtube.com
Integration by u Substitution Integral of cot^2(x)csc^2(x) dx YouTube Cot 2 X Csc X 5 The cosecant function is positive in the first and second quadrants. To find the second solution, subtract the reference angle from π π to find. For example, 1 + cot^2x =. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We have different formulas and identities in trigonometry that involve cot^2x. In this section, we will. Cot 2 X Csc X 5.
From derivativeit.com
October 5, 2020 DerivativeIt Cot 2 X Csc X 5 For example, 1 + cot^2x =. In this section, we will understand the cot^2x identity in trigonometry. We can also divide the other way. To find the second solution, subtract the reference angle from π π to find. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first. Cot 2 X Csc X 5.
From brainly.in
(5 cot x + cosec x)/(5 cot X cosec X) = 7/3, what is the value of cos Cot 2 X Csc X 5 Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We can also divide the other way. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. The cosecant function is positive in the first and second quadrants. To find the second solution, subtract the reference angle from π π to find. For example, 1 + cot^2x =. We have different formulas. Cot 2 X Csc X 5.
From www.teachoo.com
Ex 3.4, 4 cosec x = 2, find principal and general solution Cot 2 X Csc X 5 We have different formulas and identities in trigonometry that involve cot^2x. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the reference angle from π π to find. In this section, we will understand the cot^2x identity in trigonometry. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We can also divide the other. Cot 2 X Csc X 5.
From brainly.lat
Sen x + cos x • cot x = csc x Brainly.lat Cot 2 X Csc X 5 The cosecant function is positive in the first and second quadrants. We can also divide the other way. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We have different formulas and identities in trigonometry that involve cot^2x. To find the second solution, subtract the reference angle from π π to find. In this section, we. Cot 2 X Csc X 5.
From www.sarthaks.com
∫ (cosec x)^5 dx = α cosec x cot x (cosec^2 x + 3/2) + β/2 logtan x/2 Cot 2 X Csc X 5 In this section, we will understand the cot^2x identity in trigonometry. We can also divide the other way. To find the second solution, subtract the reference angle from π π to find. The cosecant function is positive in the first and second quadrants. We have different formulas and identities in trigonometry that involve cot^2x. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. Tan. Cot 2 X Csc X 5.
From www.numerade.com
SOLVEDFind each integral. ∫cotx csc^2 x d x Cot 2 X Csc X 5 We have different formulas and identities in trigonometry that involve cot^2x. The cosecant function is positive in the first and second quadrants. To find the second solution, subtract the reference angle from π π to find. We can also divide the other way. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric. Cot 2 X Csc X 5.
From www.numerade.com
SOLVEDEvaluate the integral. ∫cot^3 x csc^2 x d x Cot 2 X Csc X 5 The cosecant function is positive in the first and second quadrants. In this section, we will understand the cot^2x identity in trigonometry. We have different formulas and identities in trigonometry that involve cot^2x. For example, 1 + cot^2x =. We can also divide the other way. To find the second solution, subtract the reference angle from π π to find.. Cot 2 X Csc X 5.
From www.sarthaks.com
frac{1}{\operatorname{cosec} x\cot x}\frac{1}{\sin x}= \) (a) \( \tan Cot 2 X Csc X 5 Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. In this section, we will understand the cot^2x identity in trigonometry. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. For example, 1 + cot^2x =. The cosecant function is positive in the first and second quadrants. To find the second solution, subtract the reference angle from π π to find.. Cot 2 X Csc X 5.
From www.toppr.com
int √( cosec x cot x/cosec x + cot x). sec x/√(1 + 2 sec x) dx Cot 2 X Csc X 5 Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We can also divide the other way. To find the second solution, subtract the reference angle from π π to find. The cosecant function is positive in the first and second quadrants. In this section, we will understand the cot^2x identity in trigonometry. Use the pythagorean identity. Cot 2 X Csc X 5.
From www.toppr.com
Differentiate each of the following w.r.t.xcot^{1}(text cosec x+cot x) Cot 2 X Csc X 5 For example, 1 + cot^2x =. The cosecant function is positive in the first and second quadrants. To find the second solution, subtract the reference angle from π π to find. We can also divide the other way. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. In this section, we will understand the cot^2x identity in trigonometry. We have different formulas and identities. Cot 2 X Csc X 5.
From www.toppr.com
int √( cosec x cot x/cosec x + cot x). sec x/√(1 + 2 sec x) dx Cot 2 X Csc X 5 Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the reference angle from π π to find. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. In this section, we will understand the cot^2x identity in trigonometry. We have different formulas and identities in trigonometry that involve cot^2x. The cosecant function is positive in. Cot 2 X Csc X 5.
From www.teachoo.com
Ex 12.1, 21 Find lim x > 0 (cosec x cot x) Teachoo Cot 2 X Csc X 5 We can also divide the other way. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. For example, 1 + cot^2x =. To find the second solution, subtract the reference angle from π π to find. In this section, we. Cot 2 X Csc X 5.
From byjus.com
Q41.If mcosecx + ncotx =2 and (m^2.cosec^2x) (n^2.cot^2x)=5 then (81/m Cot 2 X Csc X 5 The cosecant function is positive in the first and second quadrants. In this section, we will understand the cot^2x identity in trigonometry. For example, 1 + cot^2x =. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. To find the second solution, subtract the reference angle from π π to find. We have different formulas and. Cot 2 X Csc X 5.
From www.teachoo.com
Question 4 cosec x = 2, find principal and general solution Cot 2 X Csc X 5 To find the second solution, subtract the reference angle from π π to find. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We can also divide the other way. We have different formulas and identities in trigonometry that involve cot^2x. The cosecant function is positive in the first and second quadrants. In this section, we. Cot 2 X Csc X 5.
From socratic.org
How do you verify the identity (cot x) / (csc x +1) = (csc x 1 Cot 2 X Csc X 5 Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. The cosecant function is positive in the first and second quadrants. We can also divide the other way. For example, 1 + cot^2x =. We have different formulas and identities in trigonometry that involve cot^2x. Use the pythagorean identity \displaystyle{{\cot}^{{2}}\theta}+{1}={{\csc}^{{2}}\theta}. To find the second solution, subtract the. Cot 2 X Csc X 5.
From mungfali.com
Sin Cos Tan CSC Cot 2 X Csc X 5 In this section, we will understand the cot^2x identity in trigonometry. We have different formulas and identities in trigonometry that involve cot^2x. Tan (θ) = sin (θ) cos (θ) that is our first trigonometric identity. We can also divide the other way. The cosecant function is positive in the first and second quadrants. For example, 1 + cot^2x =. To. Cot 2 X Csc X 5.