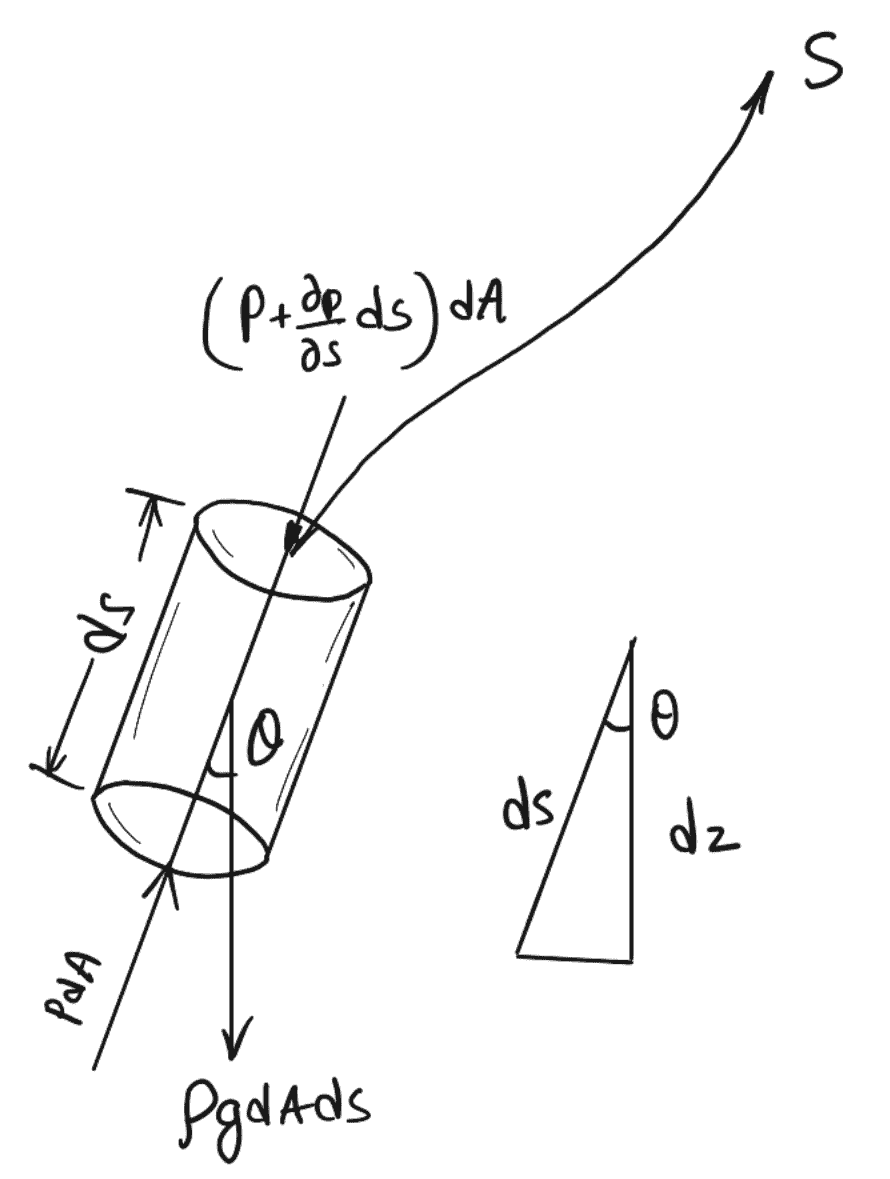
Euler's Equation Of Motion In Cartesian Coordinates at Ebony Butters blog

Euler's Equation Of Motion In Cartesian Coordinates. Using the newton's second law of motion the relationship between the velocity and pressure field for a flow of an inviscid fluid can be derived. They provide several serious challenges to obtaining the general solution for the motion of a three. Euler’s equations are that version of the equations of motion which neglect any tangential surface forces and include only the normal forces, the forces due. These equations are called euler’s equations. The euler equations state that when pressure gradients develop inside a fluid in addition to those relative to the hydrostatic equilibrium, then the. The resulting equation, in its differential form, is known as. Basic trigonometry can be used to show that the cartesian and curvilinear comnponents are related as follows. Euler’s equation in different coordinate systems can be derived either by expanding the acceleration and pressure gradient terms of eq.

Basic trigonometry can be used to show that the cartesian and curvilinear comnponents are related as follows. Euler’s equations are that version of the equations of motion which neglect any tangential surface forces and include only the normal forces, the forces due. These equations are called euler’s equations. Using the newton's second law of motion the relationship between the velocity and pressure field for a flow of an inviscid fluid can be derived. Euler’s equation in different coordinate systems can be derived either by expanding the acceleration and pressure gradient terms of eq. The euler equations state that when pressure gradients develop inside a fluid in addition to those relative to the hydrostatic equilibrium, then the. The resulting equation, in its differential form, is known as. They provide several serious challenges to obtaining the general solution for the motion of a three.

Euler's Equation of Motion in Fluid Dynamics Bernoulli's Equation

Euler's Equation Of Motion In Cartesian Coordinates The euler equations state that when pressure gradients develop inside a fluid in addition to those relative to the hydrostatic equilibrium, then the. Euler’s equations are that version of the equations of motion which neglect any tangential surface forces and include only the normal forces, the forces due. The euler equations state that when pressure gradients develop inside a fluid in addition to those relative to the hydrostatic equilibrium, then the. Using the newton's second law of motion the relationship between the velocity and pressure field for a flow of an inviscid fluid can be derived. Basic trigonometry can be used to show that the cartesian and curvilinear comnponents are related as follows. The resulting equation, in its differential form, is known as. They provide several serious challenges to obtaining the general solution for the motion of a three. These equations are called euler’s equations. Euler’s equation in different coordinate systems can be derived either by expanding the acceleration and pressure gradient terms of eq.