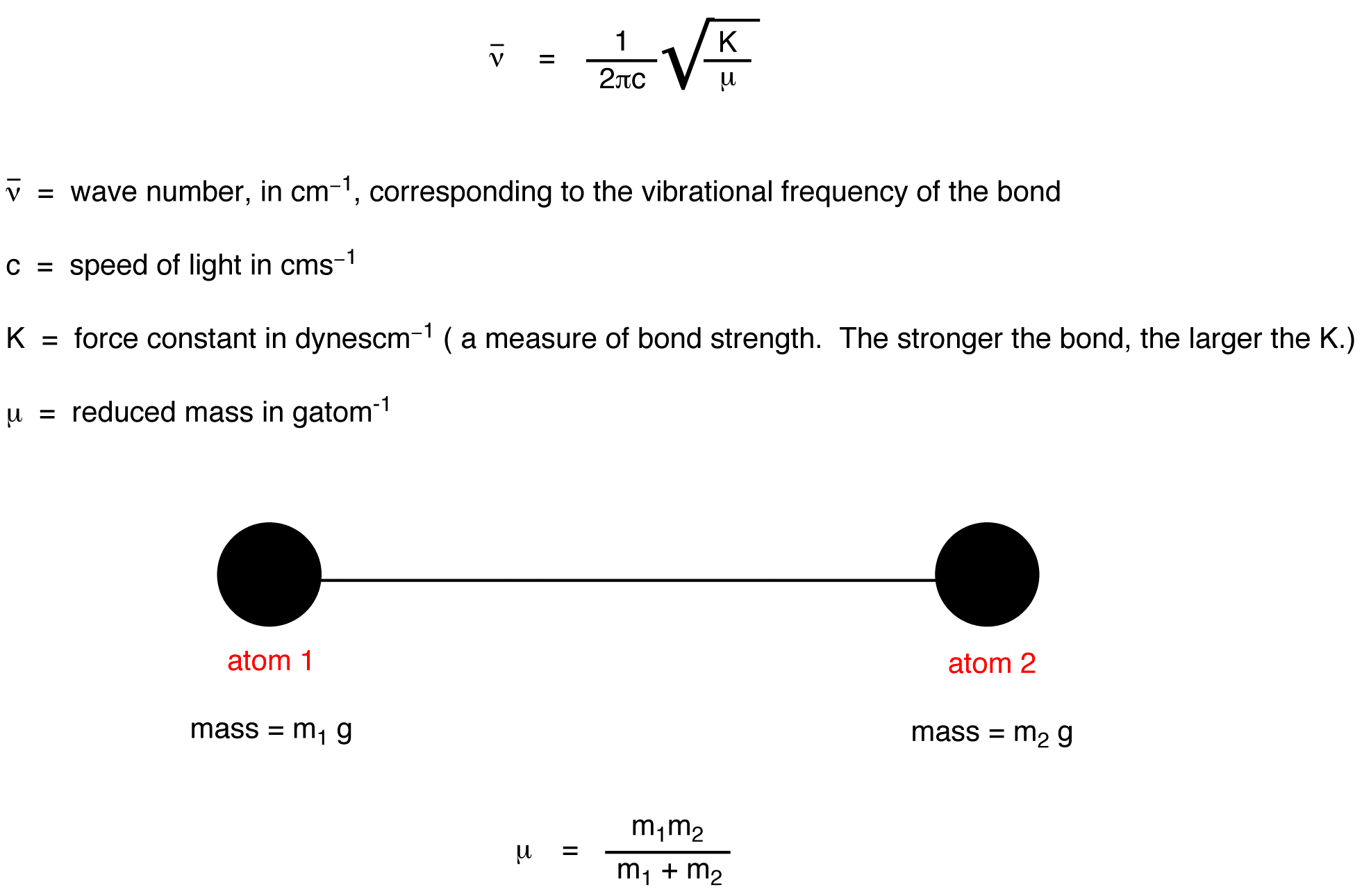Hooke's Law Matrix . Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. In its simplest form, the law defines the spring. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Understand the relation between internal material symmetries.
from chem.libretexts.org
Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. In its simplest form, the law defines the spring. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Understand the relation between internal material symmetries. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can.
Hooke’s Law Chemistry LibreTexts
Hooke's Law Matrix Understand the relation between internal material symmetries. Understand the relation between internal material symmetries. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n.
From www.researchgate.net
Hooke's law. (a) The mechanical properties of a material with defined... Download Scientific Hooke's Law Matrix However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Understand the relation between internal material symmetries. The two elastic constants are. Hooke's Law Matrix.
From www.youtube.com
Hooke's Law and Elastic Potential Energy YouTube Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. In its simplest form, the law defines the spring. Understand the relation between internal material symmetries. The two elastic constants are. Hooke's Law Matrix.
From www.worksheetsplanet.com
Hooke's Law Formula + Definition Worksheets Hooke's Law Matrix However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio. Hooke's Law Matrix.
From extrudesign.com
Hooke’s Law Definition What is Hooke’s Law? ExtruDesign Hooke's Law Matrix However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Understand the relation between internal material symmetries. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6. Hooke's Law Matrix.
From courses.lumenlearning.com
Hooke’s Law Boundless Physics Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus). Hooke's Law Matrix.
From quantumaniac.com
Quantumaniac — Hooke’s Law Known more specifically as Hooke’s... Hooke's Law Matrix However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Understand the relation between internal material symmetries. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Cauchy. Hooke's Law Matrix.
From engineerexcel.com
Hooke's Law A Complete Guide EngineerExcel Hooke's Law Matrix Understand the relation between internal material symmetries. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to. Hooke's Law Matrix.
From www.youtube.com
Concepts in 5 minutes Generalised Hooke's law matrix format isotropic materials YouTube Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Understand the relation. Hooke's Law Matrix.
From www.edrawmax.com
A Guide to Understand Hooke's Law with Diagram EdrawMax Online Hooke's Law Matrix In its simplest form, the law defines the spring. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that. Hooke's Law Matrix.
From www.youtube.com
Ch8 Example of generalized Hooke's law deriving new equation YouTube Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus). Hooke's Law Matrix.
From www.sciencefacts.net
Hooke’s Law Statement, Formula, and Diagram Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. In its simplest form, the law defines the spring. However, the alternative elastic constants k (bulk modulus). Hooke's Law Matrix.
From www.sciencefacts.net
Hooke’s Law Statement, Formula, and Diagram Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. In its simplest form, the law defines the spring. However, the alternative. Hooke's Law Matrix.
From www.slideserve.com
PPT Elastic Potential Energy & Springs PowerPoint Presentation ID3093452 Hooke's Law Matrix In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus). Hooke's Law Matrix.
From www.eigenplus.com
Hooke’s law A StressStrain Relationship Formula & Explanation Hooke's Law Matrix Understand the relation between internal material symmetries. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6. Hooke's Law Matrix.
From engineerexcel.com
Hooke's Law A Complete Guide EngineerExcel Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Understand the relation between internal material symmetries. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. However, the alternative elastic constants. Hooke's Law Matrix.
From www.slideserve.com
PPT Earthquake Seismology The stress tensor Equation of motion Hooke’s law PowerPoint Hooke's Law Matrix The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Understand the relation between internal material symmetries. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. In its simplest form, the law defines the spring. However, the alternative elastic constants. Hooke's Law Matrix.
From www.springsfast.com
Hooke’s Law and the Science Behind Springs WB Jones Hooke's Law Matrix The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus). Hooke's Law Matrix.
From www.askmattrab.com
Hooke's Law Class Eleven Physics Hooke's Law Matrix Understand the relation between internal material symmetries. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are usually expressed as the. Hooke's Law Matrix.
From thescienceandmathszone.com
Hooke's Law The Science and Maths Zone Hooke's Law Matrix However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Understand the relation between internal material symmetries. In. Hooke's Law Matrix.
From slidetodoc.com
Hookes Law Elastic Potential Energy Understandings Hookes Law Hooke's Law Matrix In its simplest form, the law defines the spring. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. Understand the relation between internal material symmetries. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. The two elastic constants are. Hooke's Law Matrix.
From thescienceandmathszone.com
Hooke's Law The Science and Maths Zone Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. In its simplest form, the law defines the spring. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio. Hooke's Law Matrix.
From www.youtube.com
Hooke's Law Strength of Materials 07 YouTube Hooke's Law Matrix The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Understand the relation between internal material symmetries. In its simplest form, the law defines the spring. Cauchy generalized hooke's law to. Hooke's Law Matrix.
From thescienceandmathszone.com
Hooke's Law The Science and Maths Zone Hooke's Law Matrix The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. In its simplest form,. Hooke's Law Matrix.
From www.slideserve.com
PPT Hooke’s Law PowerPoint Presentation, free download ID4793078 Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Understand the relation between internal material symmetries. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. In its simplest form, the. Hooke's Law Matrix.
From chem.libretexts.org
Hooke’s Law Chemistry LibreTexts Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Understand the relation between internal material symmetries. In its simplest form, the law defines the spring. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are. Hooke's Law Matrix.
From www.slideserve.com
PPT Materials Hooke’s Law PowerPoint Presentation, free download ID1414586 Hooke's Law Matrix In its simplest form, the law defines the spring. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to. Hooke's Law Matrix.
From www.youtube.com
Generalized Hooke's Law YouTube Hooke's Law Matrix In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of. Hooke's Law Matrix.
From en.wikipedia.org
Hooke's law Wikipedia Hooke's Law Matrix In its simplest form, the law defines the spring. Understand the relation between internal material symmetries. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6. Hooke's Law Matrix.
From www.bio-meca.com
GloMeca 3 Skin elasticity From Hooke's law to Young's modulusin level BioMeca Hooke's Law Matrix However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. Understand the relation between internal material symmetries. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. The two elastic constants are usually expressed as the young's modulus e and the. Hooke's Law Matrix.
From www.chegg.com
Solved 7. (Anisotropic elasticity3D Hooke's law example, 16 Hooke's Law Matrix Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus). Hooke's Law Matrix.
From calcworkshop.com
Work and Hooke's Law Hooke's Law Matrix The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to. Hooke's Law Matrix.
From albertgrokane.blogspot.com
Definition of Hooke's Law in Physics Hooke's Law Matrix In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. However, the alternative. Hooke's Law Matrix.
From www.youtube.com
(18A) Generalized Hooke's Law, Review of equilibrium and kinematic relations YouTube Hooke's Law Matrix In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the 6 components of strain. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that. Hooke's Law Matrix.
From www.sciencefacts.net
Hooke’s Law Statement, Formula, and Diagram Hooke's Law Matrix In its simplest form, the law defines the spring. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. However, the alternative elastic constants k (bulk modulus) and/or g (shear modulus) can. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to. Hooke's Law Matrix.
From www.eigenplus.com
Hooke’s law A StressStrain Relationship Formula & Explanation Hooke's Law Matrix In its simplest form, the law defines the spring. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that the 6 components of stress are linearly related to the. The two elastic constants are usually expressed as the young's modulus e and the poisson's ratio n. Cauchy generalized hooke's law to three dimensional elastic bodies and stated that. Hooke's Law Matrix.