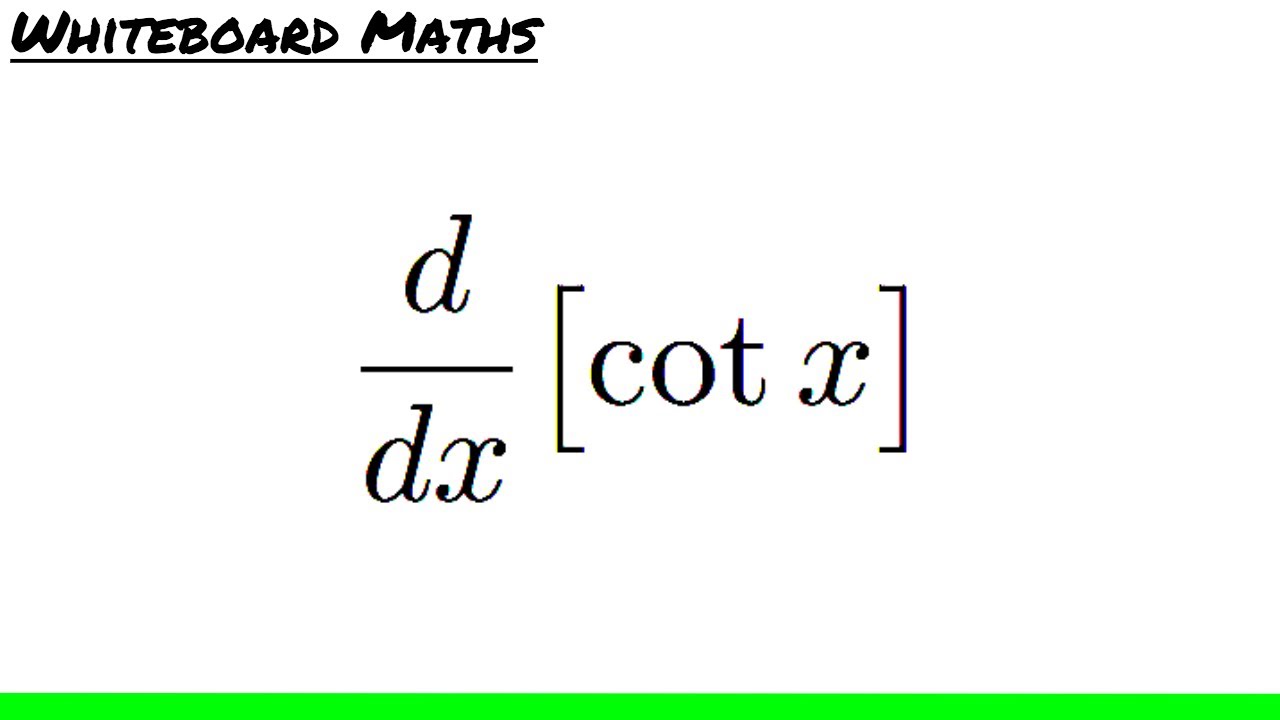Derivative Of Cotangent Proof . This derivative can be proved using limits. From derivative of sine function: From the definition of the cotangent function: In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. Where sin x ≠ 0 sin. We start by defining cot (x) as cos (x) sin (x). X = − 1 sin 2. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. From the definition of the. $\cot x = \dfrac {\cos x} {\sin x}$. X) = − csc 2.
from www.youtube.com
$\cot x = \dfrac {\cos x} {\sin x}$. X = − 1 sin 2. This derivative can be proved using limits. In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. From the definition of the cotangent function: From the definition of the. To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. From derivative of sine function: D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot.
Derivative of cot x YouTube
Derivative Of Cotangent Proof Where sin x ≠ 0 sin. X = − 1 sin 2. This derivative can be proved using limits. From the definition of the. X) = − csc 2. Where sin x ≠ 0 sin. We start by defining cot (x) as cos (x) sin (x). From the definition of the cotangent function: In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. From derivative of sine function: To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. $\cot x = \dfrac {\cos x} {\sin x}$.
From www.youtube.com
Proof The Derivative of Cotangent d/dx[cot(x)] YouTube Derivative Of Cotangent Proof Where sin x ≠ 0 sin. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. From the definition of the. This derivative can be proved using limits. To find the derivative, we use the quotient rule, which states that. Derivative Of Cotangent Proof.
From www.dailymotion.com
Calculus I Derivative of Inverse Hyperbolic Cotangent Function Derivative Of Cotangent Proof This derivative can be proved using limits. In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. X) = − csc 2. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. $\cot x = \dfrac {\cos. Derivative Of Cotangent Proof.
From en.neurochispas.com
Derivative of arccot (Inverse Cotangent) With Proof and Graphs Derivative Of Cotangent Proof To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. Where sin x ≠ 0 sin. From the definition of the cotangent. Derivative Of Cotangent Proof.
From en.neurochispas.com
Derivative of Cotangent Squared, cot^2(x) with Proof and Graphs Derivative Of Cotangent Proof X = − 1 sin 2. We start by defining cot (x) as cos (x) sin (x). From derivative of sine function: Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. D dx(cot x) = −csc2 x = −1. Derivative Of Cotangent Proof.
From www.teachoo.com
Derivative of sec1 x (Sec inverse x) Teachoo [with Video] Derivative Of Cotangent Proof To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. Where sin x ≠ 0 sin. We start. Derivative Of Cotangent Proof.
From www.youtube.com
Calc Formulas Cotangent Derivative A Second Explanation YouTube Derivative Of Cotangent Proof Where sin x ≠ 0 sin. This derivative can be proved using limits. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. $\cot x = \dfrac {\cos x} {\sin x}$. From the definition of the. In the same way. Derivative Of Cotangent Proof.
From www.slideserve.com
PPT Derivatives of Trigonometric Functions PowerPoint Presentation Derivative Of Cotangent Proof This derivative can be proved using limits. From the definition of the. $\cot x = \dfrac {\cos x} {\sin x}$. From the definition of the cotangent function: X = − 1 sin 2. From derivative of sine function: Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as,. Derivative Of Cotangent Proof.
From www.youtube.com
Derivative of Cotangent Function YouTube Derivative Of Cotangent Proof From the definition of the. X) = − csc 2. From the definition of the cotangent function: X = − 1 sin 2. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. $\cot x = \dfrac {\cos x} {\sin x}$. From derivative of sine function: Where sin x ≠ 0 sin. To find the. Derivative Of Cotangent Proof.
From www.dailymotion.com
Calculus I Derivative of Inverse Cotangent Function arccot(x) Proof Derivative Of Cotangent Proof We start by defining cot (x) as cos (x) sin (x). X = − 1 sin 2. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. To find the derivative, we use the quotient rule, which states that the. Derivative Of Cotangent Proof.
From www.youtube.com
Deriving the Tangent and Cotangent Derivatives YouTube Derivative Of Cotangent Proof X = − 1 sin 2. From derivative of sine function: Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. Where sin x ≠ 0 sin. From the definition of the cotangent function: $\cot x = \dfrac {\cos x}. Derivative Of Cotangent Proof.
From www.youtube.com
Derivative of the Inverse Hyperbolic Cotangent of the Secant Function Derivative Of Cotangent Proof In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. From the definition of the. Where sin x ≠ 0 sin. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot.. Derivative Of Cotangent Proof.
From www.teachoo.com
Example 21 Compute derivative of f(x) = cot x Teachoo Derivative Of Cotangent Proof $\cot x = \dfrac {\cos x} {\sin x}$. To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. From the definition of the cotangent function: We start by defining cot (x) as cos (x) sin (x). In. Derivative Of Cotangent Proof.
From www.youtube.com
What is the Derivative of cot^2x Derivative of cot square x YouTube Derivative Of Cotangent Proof We start by defining cot (x) as cos (x) sin (x). From the definition of the. From derivative of sine function: This derivative can be proved using limits. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can. Derivative Of Cotangent Proof.
From www.epsilonify.com
Derivative of ln(x) using First Principle of Derivatives [PROOF] Derivative Of Cotangent Proof In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. This derivative. Derivative Of Cotangent Proof.
From www.youtube.com
Proof of the derivative of tanx A StepbyStep Proof and Explanation Derivative Of Cotangent Proof D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. From the definition of the cotangent function: Where sin x ≠ 0 sin. From the definition of the. X) = − csc 2. X = − 1 sin 2. In this article, we will learn about the derivative of cot x and its formula including. Derivative Of Cotangent Proof.
From www.youtube.com
Derivative of cot(x) Proof YouTube Derivative Of Cotangent Proof Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. $\cot x = \dfrac {\cos x} {\sin x}$. X = − 1 sin 2. We start by defining cot (x) as cos (x) sin (x). D dx(cot x) = −csc2. Derivative Of Cotangent Proof.
From www.teachoo.com
Example 21 Compute derivative (i) f(x) = sin 2x Derivatives by for Derivative Of Cotangent Proof X = − 1 sin 2. X) = − csc 2. In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. From the definition of the cotangent function: From derivative of sine function: This derivative can. Derivative Of Cotangent Proof.
From www.youtube.com
Prove that the derivative of cot^(1) x= 1/(1+ x^2). Derivative of Derivative Of Cotangent Proof From derivative of sine function: Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. From the definition of the cotangent function: Where sin x ≠ 0 sin. $\cot x = \dfrac {\cos x} {\sin x}$. X = − 1. Derivative Of Cotangent Proof.
From www.epsilonify.com
What is the Derivative of cot(x)? [FULL SOLUTION] Derivative Of Cotangent Proof D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. This derivative can be proved using limits. X = − 1 sin 2. In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule. Derivative Of Cotangent Proof.
From epsilonify.com
Derivative of Hyperbolic Cotangent using First Principle of Derivatives Derivative Of Cotangent Proof D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. From the definition of the. We start by defining cot (x) as cos (x) sin (x). To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. From the definition of the cotangent function: In this article, we. Derivative Of Cotangent Proof.
From www.youtube.com
The derivative of the cot(x) YouTube Derivative Of Cotangent Proof In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. We start by defining cot (x) as cos (x) sin (x). Proof of differentiation of cot x by quotient rule to prove the derivative of cotx,. Derivative Of Cotangent Proof.
From www.youtube.com
Derivative of Cotangent Function Calculus Math Video Central YouTube Derivative Of Cotangent Proof $\cot x = \dfrac {\cos x} {\sin x}$. Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. From the definition of the. Where sin x ≠ 0 sin. From the definition of the cotangent function: In this article, we. Derivative Of Cotangent Proof.
From www.slideshare.net
Lesson 16 Inverse Trigonometric Functions Derivative Of Cotangent Proof Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. This derivative. Derivative Of Cotangent Proof.
From www.youtube.com
DERIVATIVE OF INVERSE HYPERBOLIC COTANGENT FUNCTION. YouTube Derivative Of Cotangent Proof This derivative can be proved using limits. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. X) = − csc 2. From the definition of the cotangent function: From the definition of the. We start by defining cot (x) as cos (x) sin (x). Proof of differentiation of cot x by quotient rule to. Derivative Of Cotangent Proof.
From testbook.com
Derivative of cot x Learn definition, formula, examples here Derivative Of Cotangent Proof In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. $\cot x = \dfrac {\cos x} {\sin x}$. Proof of differentiation of cot x by quotient rule. Derivative Of Cotangent Proof.
From www.youtube.com
Proof of inverse Trig Derivatives YouTube Derivative Of Cotangent Proof To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. X) = − csc 2. D dx(cot x). Derivative Of Cotangent Proof.
From buzzar-brandi.blogspot.com
Brandi's Buzzar Blog Proof Derivative cot x = csc^2 x Derivative Of Cotangent Proof This derivative can be proved using limits. In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. From. Derivative Of Cotangent Proof.
From www.youtube.com
Proof of 3 inverse trig derivatives YouTube Derivative Of Cotangent Proof Where sin x ≠ 0 sin. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. From the definition of the. In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. $\cot x = \dfrac {\cos x}. Derivative Of Cotangent Proof.
From www.dailymotion.com
Calculus I Derivative of Hyperbolic Cotangent Function coth(x Derivative Of Cotangent Proof From the definition of the. From derivative of sine function: Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. This derivative can be proved using limits. $\cot x = \dfrac {\cos x} {\sin x}$. X = − 1 sin. Derivative Of Cotangent Proof.
From www.cuemath.com
Differentiation of Trigonometric Functions Trig Derivatives Derivative Of Cotangent Proof X = − 1 sin 2. From derivative of sine function: Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. We start by defining cot (x) as cos (x) sin (x). From the definition of the cotangent function: In. Derivative Of Cotangent Proof.
From www.youtube.com
DERIVATIVE OF COTANGENT FUNCTION. YouTube Derivative Of Cotangent Proof We start by defining cot (x) as cos (x) sin (x). Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. X) = − csc 2. To find the derivative, we use the quotient rule, which states that the derivative. Derivative Of Cotangent Proof.
From www.youtube.com
Prove Derivative of Inverse Cotangent YouTube Derivative Of Cotangent Proof Proof of differentiation of cot x by quotient rule to prove the derivative of cotx, we can start by writing it as, f(x) = cot x = 1/ tan x. To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. In this article, we will learn about the derivative of cot x. Derivative Of Cotangent Proof.
From www.dailymotion.com
Calculus I Derivative of Cotangent Function cot(x) Proof video Derivative Of Cotangent Proof In this article, we will learn about the derivative of cot x and its formula including the proof of the formula using the first principle of derivatives, quotient rule, and chain rule as well. In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas. Derivative Of Cotangent Proof.
From www.youtube.com
Derivative of cot x YouTube Derivative Of Cotangent Proof From the definition of the cotangent function: $\cot x = \dfrac {\cos x} {\sin x}$. This derivative can be proved using limits. From the definition of the. In the same way that we can encapsulate the chain rule in the derivative of \(\ln u\) as \(\dfrac{d}{dx}\big(\ln u\big) = \dfrac{u'}{u}\), we can write formulas for the. To find the derivative, we. Derivative Of Cotangent Proof.
From www.cuemath.com
Derivative of Hyperbolic Functions Formula, Proof, Examples Derivative Of Cotangent Proof From derivative of sine function: X = − 1 sin 2. D dx(cot x) = −csc2 x = −1 sin2 x d d x ( cot. To find the derivative, we use the quotient rule, which states that the derivative of a quotient u. X) = − csc 2. Where sin x ≠ 0 sin. We start by defining cot. Derivative Of Cotangent Proof.