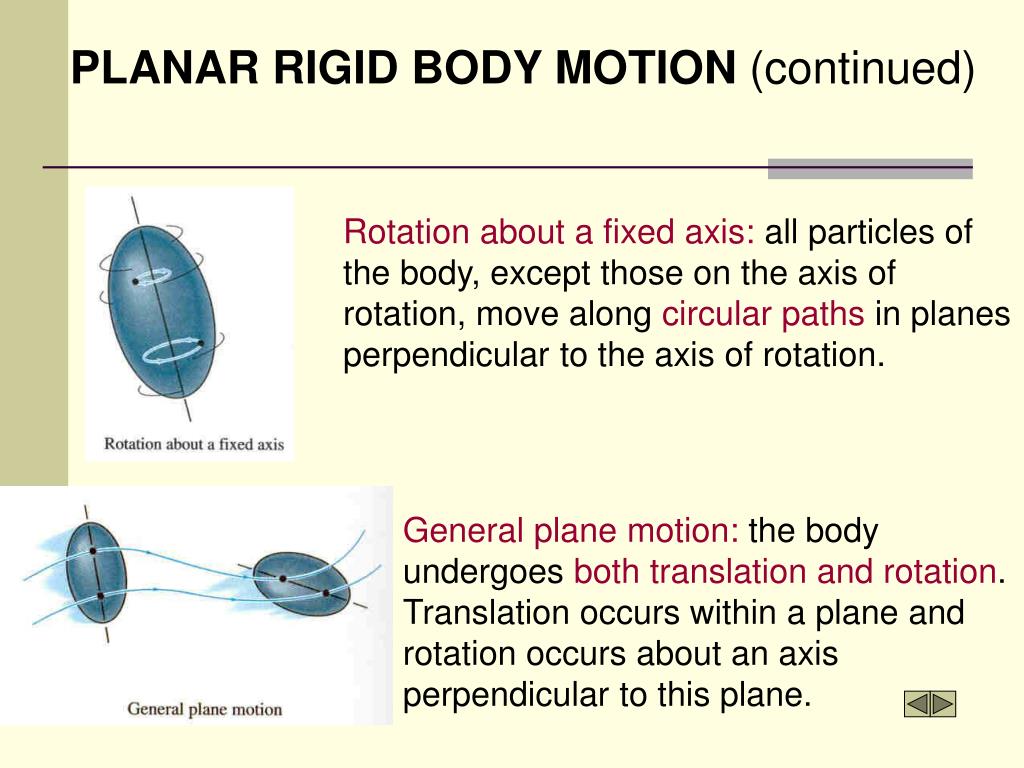
Planar Translation Definition . Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. It involves the study of movement and forces associated. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are.
from www.slideserve.com
Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. It involves the study of movement and forces associated. The prime example of this case. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion).
PPT Objectives To analyze the kinematics of a rigid body undergoing
Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. It involves the study of movement and forces associated. The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion).
From www.slideserve.com
PPT Objectives To analyze the kinematics of a rigid body undergoing Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances. Planar Translation Definition.
From www.slideserve.com
PPT PLANAR RIGID BODY MOTION TRANSLATION & ROTATION PowerPoint Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. The prime example of this case. It involves the study of movement and forces associated. This. Planar Translation Definition.
From www.slideserve.com
PPT Objectives To analyze the kinematics of a rigid body undergoing Planar Translation Definition It involves the study of movement and forces associated. The prime example of this case. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). 4.1.1 planar translations. Planar Translation Definition.
From www.youtube.com
Dynamics Lecture 23 Rigid body planar motion Translation YouTube Planar Translation Definition This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. The prime example of this case. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). 4.1.1 planar translations let the coordinates of. Planar Translation Definition.
From www.youtube.com
3 Types of Transformations *Translations Reflections & Rotations *Math Planar Translation Definition The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and. Planar Translation Definition.
From www.youtube.com
Planar Motion What are Translation, rotation, and general plane motion Planar Translation Definition Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. It involves the study of movement and forces associated. This transformation is also known as 2d rigid body. Planar Translation Definition.
From www.studypool.com
SOLUTION What is Planar Imaging? Definition, Types, Examples Studypool Planar Translation Definition Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving. Planar Translation Definition.
From www.slideserve.com
PPT Objectives To analyze the kinematics of a rigid body undergoing Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. The prime example of this case. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. This transformation is also known as 2d rigid body motion. Planar Translation Definition.
From byjus.com
What is Translation in Math? (Definition, Properties, Examples) BYJUS Planar Translation Definition This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. The prime example of this case. Analysis of a rigid body. Planar Translation Definition.
From www.youtube.com
Transformation Translation Examples (Basic Geometry Concepts) YouTube Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the. Planar Translation Definition.
From www.youtube.com
Video 11 Planar of a Rigid Body EoM Translation Example 1 Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. It involves the study of movement and forces associated. The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. This. Planar Translation Definition.
From thirdspacelearning.com
Translation GCSE Maths Steps, Examples & Worksheet Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate. Planar Translation Definition.
From www.slideserve.com
PPT Chapter 16 Planar Kinematics of a Rigid Body PowerPoint Planar Translation Definition It involves the study of movement and forces associated. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Analysis of. Planar Translation Definition.
From www.youtube.com
Lecture 13 Example 5 Planar Rigid Body Motion Translation and Planar Translation Definition The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. It involves the study of movement and forces associated. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not. Planar Translation Definition.
From www.youtube.com
Rigid Body Planar Translation Two Particles YouTube Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). It involves. Planar Translation Definition.
From www.youtube.com
Planar Translation n t coordinates YouTube Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). It involves. Planar Translation Definition.
From www.slideserve.com
PPT Objectives To analyze the kinematics of a rigid body undergoing Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. It involves the study of movement and forces associated. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the. Planar Translation Definition.
From www.slideserve.com
PPT Chapter 16 Planar Kinematics of a Rigid Body PowerPoint Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. The prime example of this case. Analysis of a rigid body. Planar Translation Definition.
From studylib.net
Sections 16.116.3 Department of Mechanical Engineering Planar Translation Definition Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). The prime example of this case. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. It involves the study of movement and. Planar Translation Definition.
From byjus.com
What is Translation in Math? (Definition, Properties, Examples) BYJUS Planar Translation Definition The prime example of this case. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x =. Planar Translation Definition.
From www.youtube.com
[2015] Dynamics 30 Equations of Motion for Planar Motion. Translation Planar Translation Definition This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. The prime example of this case. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some. Planar Translation Definition.
From www.slideserve.com
PPT Today’s Objectives Students will be able to analyze the Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. It involves the study of movement and forces associated. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. The prime example of this case. Some rigid bodies will translate but not rotate (translational systems), some will. Planar Translation Definition.
From www.researchgate.net
Illustration of the planar translation, Δr, using the centroid of the Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). It involves the study of movement and forces associated. 4.1.1 planar translations let the coordinates of a point. Planar Translation Definition.
From www.slideserve.com
PPT Objectives To analyze the kinematics of a rigid body undergoing Planar Translation Definition This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x =. Planar Translation Definition.
From slidetodoc.com
PLANAR RIGID BODY MOTION TRANSLATION ROTATION Todays Objectives Planar Translation Definition It involves the study of movement and forces associated. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. The prime. Planar Translation Definition.
From byjus.com
What is Translation in Math? (Definition, Properties, Examples) BYJUS Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. It involves the study of movement and forces associated. Analysis of. Planar Translation Definition.
From www.slideserve.com
PPT Today’s Objectives Students will be able to analyze the Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. The prime example of this case. It involves the study of movement and forces associated. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not. Planar Translation Definition.
From www.youtube.com
Planar Equation of Motion Translation (Rectilinear and Planar Translation Definition Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). It involves the study of movement and forces associated. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. This transformation is also known as 2d rigid body. Planar Translation Definition.
From www.slideserve.com
PPT Objectives To analyze the kinematics of a rigid body undergoing Planar Translation Definition The prime example of this case. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. It involves the study of movement and forces associated. Some. Planar Translation Definition.
From www.youtube.com
[2015] Dynamics 23 Rigid Body Planar Motion. Translation [with closed Planar Translation Definition Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. Analysis of. Planar Translation Definition.
From www.slideserve.com
PPT Objectives To analyze the kinematics of a rigid body undergoing Planar Translation Definition Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since. Planar Translation Definition.
From www.slideserve.com
PPT 92 Translations PowerPoint Presentation, free download ID2484325 Planar Translation Definition It involves the study of movement and forces associated. Analysis of a rigid body undergoing general planar motion, incorporating both translation and rotation. Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). This transformation is also known as 2d rigid body. Planar Translation Definition.
From www.youtube.com
Planar Meaning, Definition, and Examples YouTube Planar Translation Definition Some rigid bodies will translate but not rotate (translational systems), some will rotate but not translate (fixed axis rotation), and some will rotate and translate (general planar motion). It involves the study of movement and forces associated. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t. Planar Translation Definition.
From www.researchgate.net
a), the subchain PP generates the 2D group of planar translations {T Planar Translation Definition It involves the study of movement and forces associated. The prime example of this case. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation (since euclidean distances are. 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let. Planar Translation Definition.
From www.youtube.com
Video 12 Planar of a Rigid Body EoM Translation Example 2 Planar Translation Definition 4.1.1 planar translations let the coordinates of a point in the moving body m be denoted by the vector x = (x;y) t , and let the coordinates of the. It involves the study of movement and forces associated. The prime example of this case. This transformation is also known as 2d rigid body motion or the 2d euclidean transformation. Planar Translation Definition.