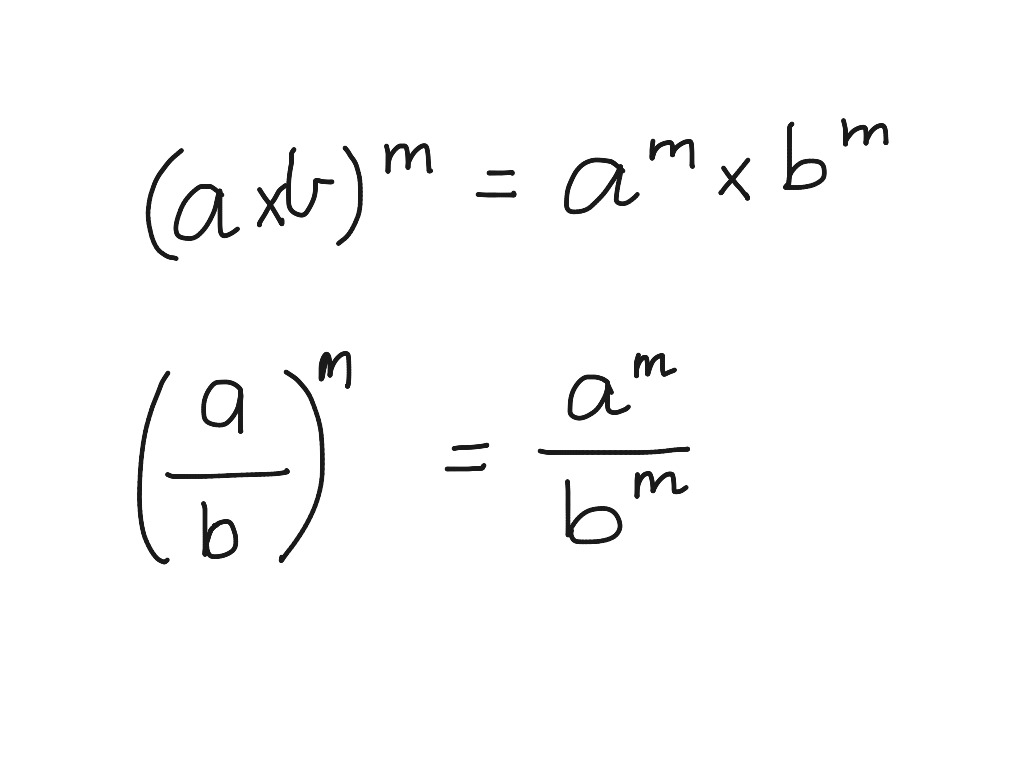Index Law Wiki . Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Understanding the index laws with practical examples and applications.00:00. Let $a^n$ be defined as the power of an element. Index laws for semigroup sum of indices. The index provides data on eight dimensions of the rule of law: Let $\struct {s, \circ}$ be a semigroup. Let $\struct {s, \circ}$ be a semigroup. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f.
from www.showme.com
Let $a^n$ be defined as the power of an element. Index laws for semigroup sum of indices. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Understanding the index laws with practical examples and applications.00:00. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $\struct {s, \circ}$ be a semigroup. Let $\struct {s, \circ}$ be a semigroup. The index provides data on eight dimensions of the rule of law:
Fourth index law Math, indices, fourth index law ShowMe
Index Law Wiki Let $a^n$ be defined as the power of an element. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Understanding the index laws with practical examples and applications.00:00. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Index laws for semigroup sum of indices. The index provides data on eight dimensions of the rule of law: Let $\struct {s, \circ}$ be a semigroup. Let $a^n$ be defined as the power of an element. Let $\struct {s, \circ}$ be a semigroup.
From www.youtube.com
Laws of Indices with solved Examples SHS 2 CORE MATH YouTube Index Law Wiki For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $\struct {s, \circ}$ be a semigroup. Let $\struct {s, \circ}$ be a semigroup. Understanding the index laws with practical examples and applications.00:00. The index provides data on eight dimensions of the rule of law: Let (f, +, ∘) (f, +, ∘) be a field. Index Law Wiki.
From www.youtube.com
The Fourth Index Law (Raising power to another power) YouTube Index Law Wiki For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Understanding the index laws with practical examples and applications.00:00. The index provides data on eight dimensions of the rule of law: Index laws for semigroup. Index Law Wiki.
From www.youtube.com
Third Index Law YouTube Index Law Wiki Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Index laws for semigroup sum of indices. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $a^n$ be defined as the power of an element. Let $\struct. Index Law Wiki.
From www.slideshare.net
Index Notation Index Law Wiki Let $\struct {s, \circ}$ be a semigroup. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Understanding the index laws with practical examples and applications.00:00. Let $a^n$ be defined as the power of an element. Let (f, +, ∘) (f, +, ∘) be. Index Law Wiki.
From www.youtube.com
S2 Ex8A Index Law 5 Bracket with Fraction YouTube Index Law Wiki Let $\struct {s, \circ}$ be a semigroup. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $\struct {s, \circ}$ be a semigroup. Let $a^n$ be defined as the power of an element. Understanding the index laws with practical examples and applications.00:00. The index provides data on eight dimensions. Index Law Wiki.
From mr-mathematics.com
Applying the Rules of Indices in ALevel Mathematics Index Law Wiki Index laws for semigroup sum of indices. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. The index provides data on eight dimensions of the rule of law: Let $\struct {s, \circ}$ be a semigroup. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f. Index Law Wiki.
From www.pinterest.co.kr
Learn the Laws of Indices Index Law Wiki Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $a^n$ be defined as the power of an element. Understanding the index laws with practical examples and applications.00:00. Let $\struct {s, \circ}$ be a semigroup. Let $\struct {s, \circ}$ be a semigroup. The index provides data on eight dimensions. Index Law Wiki.
From www.youtube.com
Index Laws 4&5 With Examples YouTube Index Law Wiki Let $\struct {s, \circ}$ be a semigroup. Index laws for semigroup sum of indices. Let $\struct {s, \circ}$ be a semigroup. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f. Index Law Wiki.
From www.youtube.com
Laws of indices (part 1) YouTube Index Law Wiki Index laws for semigroup sum of indices. Let $a^n$ be defined as the power of an element. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Understanding the index laws with practical examples and applications.00:00. Let $\struct {s, \circ}$ be a semigroup. The index provides data on eight dimensions of the rule of law:. Index Law Wiki.
From www.showme.com
Topic Index Laws ShowMe Online Learning Index Law Wiki Understanding the index laws with practical examples and applications.00:00. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. The index provides data on eight dimensions of the rule. Index Law Wiki.
From www.youtube.com
Index Laws 1, 2 and 3 YouTube Index Law Wiki Index laws for semigroup sum of indices. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Understanding the index laws with practical examples and applications.00:00. Let $\struct {s, \circ}$ be a semigroup. Let $\struct. Index Law Wiki.
From www.youtube.com
Laws of indices Algebra YouTube Index Law Wiki Index laws for semigroup sum of indices. Let $\struct {s, \circ}$ be a semigroup. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Understanding the index laws with practical examples and applications.00:00. Let $\struct. Index Law Wiki.
From www.youtube.com
USING INDEX LAWS TO SOLVE EQUATIONS YouTube Index Law Wiki For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1. Index Law Wiki.
From thirdspacelearning.com
Laws Of Indices GCSE Maths Steps, Examples & Worksheet Index Law Wiki Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let $a^n$ be defined as the power of an element. The index provides data on eight dimensions of the rule of law: Let (f, +, ∘) (f, +, ∘) be a field with zero. Index Law Wiki.
From www.youtube.com
Laws of indices (part 2) YouTube Index Law Wiki Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $\struct {s, \circ}$ be a semigroup. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Understanding the index laws with practical examples and applications.00:00. Let f∗ = f ∖0f f ∗ = f. Index Law Wiki.
From www.youtube.com
First index law YouTube Index Law Wiki For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $\struct {s, \circ}$ be a semigroup. Index laws for semigroup sum of indices. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let $a^n$ be defined as. Index Law Wiki.
From www.slideserve.com
PPT Lesson 2 Laws of Indices PowerPoint Presentation, free download Index Law Wiki Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $a^n$ be defined as the power of an element. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set. Index Law Wiki.
From www.slideserve.com
PPT Indices PowerPoint Presentation, free download ID3466736 Index Law Wiki Let $a^n$ be defined as the power of an element. The index provides data on eight dimensions of the rule of law: Index laws for semigroup sum of indices. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $\struct {s, \circ}$ be a semigroup. For $a \in s$,. Index Law Wiki.
From mungfali.com
Index Laws Explained Index Law Wiki Index laws for semigroup sum of indices. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $\struct {s, \circ}$ be a semigroup. Let $\struct {s, \circ}$ be a semigroup. The index provides data on eight dimensions of the rule of law: Let (f, +, ∘) (f, +, ∘) be a field with zero. Index Law Wiki.
From corbettmaths.com
Laws of Indices Algebra Video Corbettmaths Index Law Wiki Let $a^n$ be defined as the power of an element. Let $\struct {s, \circ}$ be a semigroup. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Understanding the index laws with practical examples and applications.00:00. Let $\struct {s, \circ}$ be a semigroup. For $a \in s$, let $\circ^n a. Index Law Wiki.
From www.youtube.com
Index Law 1 Multiplying Powers YouTube Index Law Wiki The index provides data on eight dimensions of the rule of law: Let $\struct {s, \circ}$ be a semigroup. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power.. Index Law Wiki.
From www.youtube.com
Index Law 3 and the Zero Power Rule With Examples YouTube Index Law Wiki Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let $\struct {s, \circ}$ be a semigroup. The index provides data on eight dimensions of the rule of law: Let $a^n$ be defined as the power of an element. Let $\struct {s, \circ}$ be. Index Law Wiki.
From www.youtube.com
Index Laws Division Law Examples and Practise YouTube Index Law Wiki Understanding the index laws with practical examples and applications.00:00. Let $\struct {s, \circ}$ be a semigroup. The index provides data on eight dimensions of the rule of law: Let $a^n$ be defined as the power of an element. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $\struct {s, \circ}$ be a semigroup.. Index Law Wiki.
From www.youtube.com
Index Law 4 examples YouTube Index Law Wiki Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Index laws for semigroup sum of indices. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $a^n$ be defined as the power of an element. Let $\struct. Index Law Wiki.
From pt.slideshare.net
Index laws ppt Index Law Wiki Index laws for semigroup sum of indices. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $\struct {s, \circ}$ be a semigroup. Let $\struct {s, \circ}$ be a semigroup. Understanding the index laws with practical examples and applications.00:00. The index provides data on eight dimensions of the rule. Index Law Wiki.
From www.youtube.com
The First Index Law and Examples YouTube Index Law Wiki Let $\struct {s, \circ}$ be a semigroup. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Understanding the index laws with practical examples and applications.00:00. Index laws for semigroup sum of indices. For $a \in s$, let $\circ^n a = a^n$ be defined. Index Law Wiki.
From www.youtube.com
4 6th Index Law YouTube Index Law Wiki Let $\struct {s, \circ}$ be a semigroup. Index laws for semigroup sum of indices. Let $a^n$ be defined as the power of an element. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let $\struct {s, \circ}$ be a semigroup. For $a \in. Index Law Wiki.
From www.showme.com
Fourth index law Math, indices, fourth index law ShowMe Index Law Wiki Let $\struct {s, \circ}$ be a semigroup. The index provides data on eight dimensions of the rule of law: Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Understanding the index laws with practical. Index Law Wiki.
From www.mathlobby.com
Math Lobby Secondary Math Laws of Indices Index Law Wiki Let $a^n$ be defined as the power of an element. Understanding the index laws with practical examples and applications.00:00. The index provides data on eight dimensions of the rule of law: Let $\struct {s, \circ}$ be a semigroup. Let $\struct {s, \circ}$ be a semigroup. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f. Index Law Wiki.
From www.youtube.com
Index Law 3 YouTube Index Law Wiki For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $a^n$ be defined as the power of an element. Let $\struct {s, \circ}$ be a semigroup. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Index laws. Index Law Wiki.
From www.youtube.com
Laws of Indices Algebra Revision for Maths GCSE and iGCSE YouTube Index Law Wiki For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $a^n$ be defined as the power of an element. Index laws for semigroup sum of indices. Let $\struct {s, \circ}$ be a semigroup. Understanding. Index Law Wiki.
From www.youtube.com
Sixth Index Law YouTube Index Law Wiki Let $\struct {s, \circ}$ be a semigroup. Index laws for semigroup sum of indices. The index provides data on eight dimensions of the rule of law: Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let $\struct {s, \circ}$ be a semigroup. Let. Index Law Wiki.
From www.youtube.com
Law of indices (all index laws) Math YouTube Index Law Wiki Let $a^n$ be defined as the power of an element. Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. The index provides data on eight dimensions of the rule of law: Index laws for semigroup sum of indices. For $a \in s$, let. Index Law Wiki.
From www.studocu.com
01 Formula Sheet index laws Common Indices The terms indices (or Index Law Wiki The index provides data on eight dimensions of the rule of law: Let $a^n$ be defined as the power of an element. Let $\struct {s, \circ}$ be a semigroup. For $a \in s$, let $\circ^n a = a^n$ be defined as the $n$th power. Let $\struct {s, \circ}$ be a semigroup. Index laws for semigroup sum of indices. Understanding the. Index Law Wiki.
From www.youtube.com
Introduction to Index Laws 2 YouTube Index Law Wiki Let f∗ = f ∖0f f ∗ = f ∖ 0 f denote the set of elements of f f without the zero 0f 0 f. Let $\struct {s, \circ}$ be a semigroup. Let (f, +, ∘) (f, +, ∘) be a field with zero 0f 0 f and unity 1f 1 f. Let $\struct {s, \circ}$ be a semigroup.. Index Law Wiki.