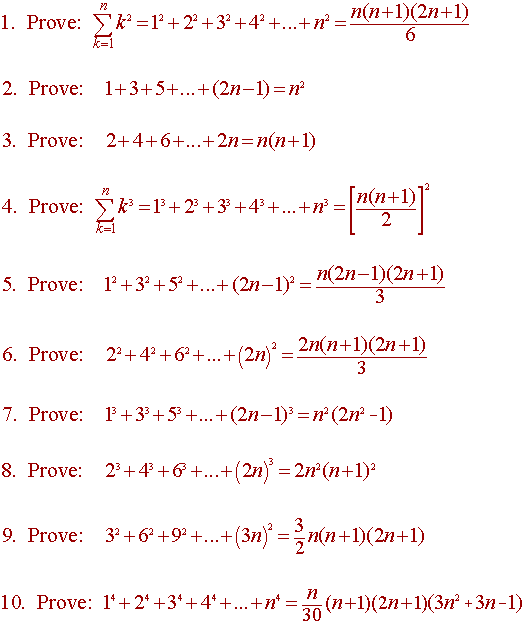Induction Math Proof Examples . The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Let’s look at a few examples of proof by induction. It has only 2 steps: Here is a typical example of such an identity: Show it is true for the first one. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Show that if any one is true then the next one is true. Solved examples on mathematical induction. Mathematical induction is a special way of proving things. In these examples, we will structure our proofs explicitly to label the base case, inductive. In order to prove a mathematical statement involving integers, we may use the following template: 1 + 2 + 3 + ⋯. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6.
from www.pleacher.com
In these examples, we will structure our proofs explicitly to label the base case, inductive. For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Show it is true for the first one. It has only 2 steps: Let’s look at a few examples of proof by induction. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Here is a typical example of such an identity: Show that if any one is true then the next one is true. Solved examples on mathematical induction.
Proof By Induction
Induction Math Proof Examples Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. 1 + 2 + 3 + ⋯. Let’s look at a few examples of proof by induction. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. In these examples, we will structure our proofs explicitly to label the base case, inductive. Show that if any one is true then the next one is true. Here is a typical example of such an identity: Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. It has only 2 steps: Show it is true for the first one. Solved examples on mathematical induction. Mathematical induction is a special way of proving things. In order to prove a mathematical statement involving integers, we may use the following template: For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6.
From www.slideserve.com
PPT Chapter 4 Sequences and Mathematical Induction PowerPoint Induction Math Proof Examples Here is a typical example of such an identity: The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. In these examples, we will structure our proofs explicitly to label the base case, inductive. 1 + 2 + 3 + ⋯. Suppose. Induction Math Proof Examples.
From calcworkshop.com
Principle of Mathematical Induction (5 Amazing Examples!) Induction Math Proof Examples Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Solved examples on mathematical induction. Show that if any one is true then the next one is true. Proof by induction. Induction Math Proof Examples.
From www.youtube.com
Proof by Induction Sum of series Example ExamSolutions YouTube Induction Math Proof Examples In these examples, we will structure our proofs explicitly to label the base case, inductive. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Let’s look at a few examples of proof by induction. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Mathematical induction. Induction Math Proof Examples.
From www.slideshare.net
mathematical induction Induction Math Proof Examples Here is a typical example of such an identity: For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. It has only. Induction Math Proof Examples.
From www.slideserve.com
PPT Proof by mathematical induction PowerPoint Presentation, free Induction Math Proof Examples In these examples, we will structure our proofs explicitly to label the base case, inductive. Show it is true for the first one. Mathematical induction is a special way of proving things. 1 + 2 + 3 + ⋯. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. In order to prove a mathematical statement involving integers, we. Induction Math Proof Examples.
From www.chegg.com
Solved a. Use mathematical induction to prove that for any n Induction Math Proof Examples It has only 2 steps: For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Show it is true for the first one. Let’s look at a few examples of proof by induction. In order to prove a mathematical statement involving integers, we may. Induction Math Proof Examples.
From www.slideserve.com
PPT Proof by Induction PowerPoint Presentation, free download ID Induction Math Proof Examples It has only 2 steps: Solved examples on mathematical induction. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Here is a typical example of such an identity: Mathematical induction is a special way of proving things. In these examples, we. Induction Math Proof Examples.
From www.youtube.com
Proof by Induction Example 1 YouTube Induction Math Proof Examples Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Solved examples on mathematical induction. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof,. Induction Math Proof Examples.
From www.pleacher.com
Proof By Induction Induction Math Proof Examples Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. It has only 2 steps: Let’s look at a few examples of proof by induction. 1 + 2 + 3 + ⋯. Mathematical induction is a special way of proving things. In these examples, we will structure our proofs explicitly to label the base case, inductive. Show that if. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. 1 + 2 + 3 + ⋯. Show that if any one. Induction Math Proof Examples.
From mathsathome.com
How to do Proof by Induction with Matrices Induction Math Proof Examples For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Mathematical induction is a special way of proving things. The proof by. Induction Math Proof Examples.
From www.slideserve.com
PPT Principle of Strong Mathematical Induction PowerPoint Induction Math Proof Examples Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. 1 + 2 + 3 + ⋯. In order. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples Let’s look at a few examples of proof by induction. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Here is a typical example of such an identity: Solved examples on mathematical induction. In order to prove a mathematical statement involving integers, we may use the following template: Proof by induction — a method to prove statements by. Induction Math Proof Examples.
From www.youtube.com
How to Write a Mathematical Induction Proof with a Summation YouTube Induction Math Proof Examples Show that if any one is true then the next one is true. Show it is true for the first one. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. In order to prove a mathematical statement involving integers, we may. Induction Math Proof Examples.
From www.youtube.com
Proof by Mathematical Induction How to do a Mathematical Induction Induction Math Proof Examples Show that if any one is true then the next one is true. Solved examples on mathematical induction. Here is a typical example of such an identity: The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. In order to prove a. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. 1 + 2 + 3 + ⋯. Show it is true for the first one. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first. Induction Math Proof Examples.
From www.pleacher.com
Proof By Induction Induction Math Proof Examples Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Show it is true for the first one. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. Mathematical induction is a special way of proving things. In order to prove a mathematical statement involving integers, we may use the following. Induction Math Proof Examples.
From www.youtube.com
Mathematical Induction Examples Solutions YouTube Induction Math Proof Examples Show that if any one is true then the next one is true. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Let’s look at a few examples of proof by induction. 1 + 2 + 3 + ⋯. Mathematical induction. Induction Math Proof Examples.
From mathsathome.com
How to do Proof by Induction with Matrices Induction Math Proof Examples For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Solved examples on mathematical induction. Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples In these examples, we will structure our proofs explicitly to label the base case, inductive. It has only 2 steps: Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Solved examples on mathematical induction. 1 + 2 + 3 + ⋯. For all n ≥ 1, prove. Induction Math Proof Examples.
From www.alevelh2maths.com
5 Steps Mathematical Induction Template Summary ALevel H2 Maths Induction Math Proof Examples Mathematical induction is a special way of proving things. Solved examples on mathematical induction. Show that if any one is true then the next one is true. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Let’s look at a few. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. Mathematical induction is a special way of proving things. For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Show that if any one is true. Induction Math Proof Examples.
From www.youtube.com
Induction proof for a summation identity YouTube Induction Math Proof Examples In order to prove a mathematical statement involving integers, we may use the following template: The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. It has only 2 steps: Show that if any one is true then the next one is. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples Solved examples on mathematical induction. Let’s look at a few examples of proof by induction. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. The proof by mathematical induction. Induction Math Proof Examples.
From mathsathome.com
How to do Proof by Mathematical Induction for Divisibility Induction Math Proof Examples The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Show it is true for the first one. Show that if any one is true then the next one is true. Proof by induction — a method to prove statements by showing. Induction Math Proof Examples.
From www.slideserve.com
PPT Proof by mathematical induction PowerPoint Presentation, free Induction Math Proof Examples Suppose p(n), ∀n ≥ n0, n, n0 ∈ z + be. Show that if any one is true then the next one is true. Show it is true for the first one. Mathematical induction is a special way of proving things. In these examples, we will structure our proofs explicitly to label the base case, inductive. Here is a typical. Induction Math Proof Examples.
From www.studypool.com
SOLUTION Strong induction Studypool Induction Math Proof Examples Show that if any one is true then the next one is true. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. For all n ≥ 1, prove that, 1 2 + 2 2 + 3 2 +….+n 2 = {n(n + 1) (2n + 1)} / 6. Mathematical induction is. Induction Math Proof Examples.
From www.youtube.com
Proof by Mathematical Induction How to do a Mathematical Induction Induction Math Proof Examples Let’s look at a few examples of proof by induction. In these examples, we will structure our proofs explicitly to label the base case, inductive. In order to prove a mathematical statement involving integers, we may use the following template: Mathematical induction is a special way of proving things. Mathematical induction can be used to prove that an identity is. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. Let’s look at a few examples of proof by induction. Show it is true for the first one. Here is a typical example of such an identity: Solved examples on mathematical induction. Mathematical induction is a special way of proving things. Suppose. Induction Math Proof Examples.
From www.slideserve.com
PPT Proof by mathematical induction PowerPoint Presentation, free Induction Math Proof Examples The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Solved examples on mathematical induction. Let’s look at a few examples of proof by induction. Show that if any one is true then the next one is true. In order to prove. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples 1 + 2 + 3 + ⋯. Solved examples on mathematical induction. It has only 2 steps: Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Mathematical induction is a special way of proving things. Let’s look at a few examples of proof by induction. In these. Induction Math Proof Examples.
From mathsathome.com
How to do Proof by Mathematical Induction for Divisibility Induction Math Proof Examples In order to prove a mathematical statement involving integers, we may use the following template: Here is a typical example of such an identity: The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition, and proof by. Let’s look at a few examples of proof. Induction Math Proof Examples.
From www.slideserve.com
PPT Mathematical Induction PowerPoint Presentation, free download Induction Math Proof Examples Let’s look at a few examples of proof by induction. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. 1 + 2 + 3 + ⋯. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as the direct proof, proof by contraposition,. Induction Math Proof Examples.
From www.youtube.com
Mathematical Induction Proof with Recursively Defined Function YouTube Induction Math Proof Examples It has only 2 steps: Show that if any one is true then the next one is true. Solved examples on mathematical induction. Mathematical induction can be used to prove that an identity is valid for all integers n ≥ 1. The proof by mathematical induction (simply known as induction) is a fundamental proof technique that is as important as. Induction Math Proof Examples.
From www.linquip.com
Mathematical Induction Calculator A Comprehensive Guide on How It Induction Math Proof Examples Let’s look at a few examples of proof by induction. Here is a typical example of such an identity: Proof by induction — a method to prove statements by showing a logical progression of justifiable steps by first asserting a hypothesis. Show that if any one is true then the next one is true. Solved examples on mathematical induction. The. Induction Math Proof Examples.