Math Partition Refinement at Rita Ware blog

Math Partition Refinement. Upper and lower sums of different partitions¶ if we take any two partitions of $[a,b]$, say $p_1$ and $p_2$, then we can combine their numbers to make a partition that is a refinement of both. We say that $q(y, s)$ is a refinement. Another partition q of the given interval [a, b] is defined as a refinement of the partitionp, if q contains all the points of p. Given any finite (positive) number of partitions \({\mathcal p}_1,\ldots,{\mathcal p}_n\), of \(r\), there is a grid partition \(\mathcal g\) of \(r\) which is a refinement of. Every point of p *is a point of p , then p * is said. Suppose that two partitions $p(x, t)$ and $q(y, s)$ are both partitions of the interval $[a, b]$. Let $p$, $p'$ be partitions at $[a,b]$. A refinement of the partition p is another partition p' that contains all the points from p and some additional points, again sorted by order of magnitude. Ø refinement of a partition let p and p * be two partitions of an interval [ ab , ] such that pp ì * i.e. We say that $p'$ is a refinement of $p$ if $p'$ $\supseteq$ $p$.

Another partition q of the given interval [a, b] is defined as a refinement of the partitionp, if q contains all the points of p. Given any finite (positive) number of partitions \({\mathcal p}_1,\ldots,{\mathcal p}_n\), of \(r\), there is a grid partition \(\mathcal g\) of \(r\) which is a refinement of. Every point of p *is a point of p , then p * is said. Suppose that two partitions $p(x, t)$ and $q(y, s)$ are both partitions of the interval $[a, b]$. Upper and lower sums of different partitions¶ if we take any two partitions of $[a,b]$, say $p_1$ and $p_2$, then we can combine their numbers to make a partition that is a refinement of both. We say that $p'$ is a refinement of $p$ if $p'$ $\supseteq$ $p$. Ø refinement of a partition let p and p * be two partitions of an interval [ ab , ] such that pp ì * i.e. We say that $q(y, s)$ is a refinement. A refinement of the partition p is another partition p' that contains all the points from p and some additional points, again sorted by order of magnitude. Let $p$, $p'$ be partitions at $[a,b]$.

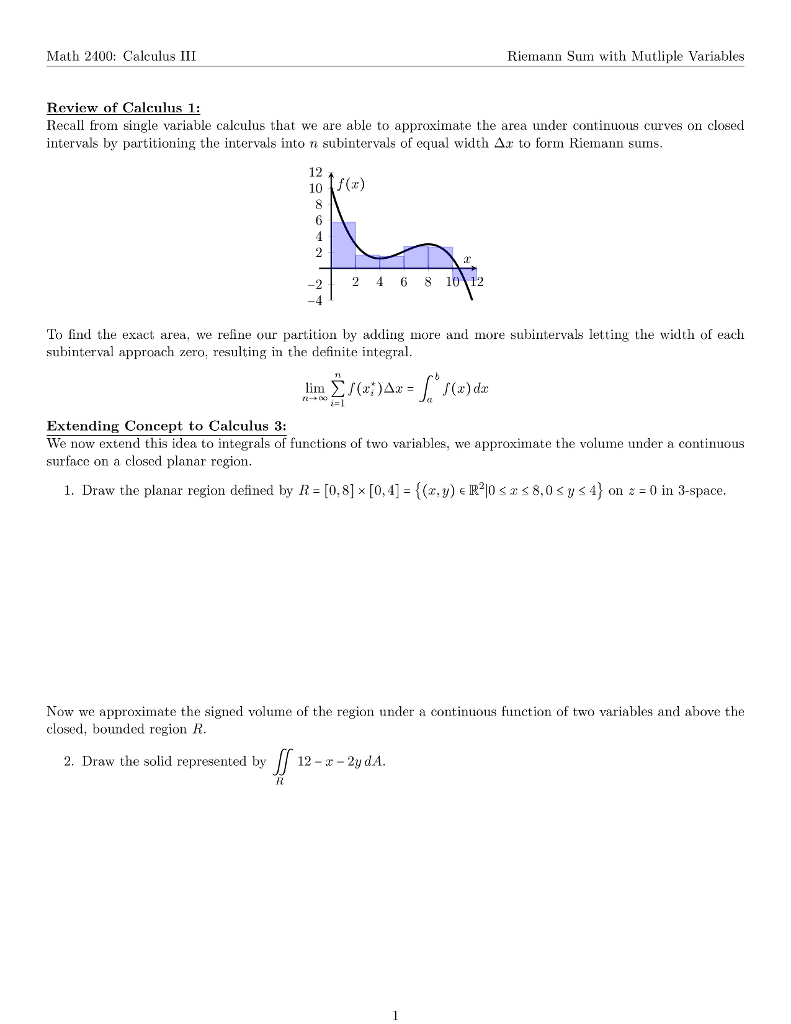
Solved Math 2100 Calculus III Riemann Sum with Mutliple Va

Math Partition Refinement We say that $p'$ is a refinement of $p$ if $p'$ $\supseteq$ $p$. We say that $q(y, s)$ is a refinement. Every point of p *is a point of p , then p * is said. Another partition q of the given interval [a, b] is defined as a refinement of the partitionp, if q contains all the points of p. Given any finite (positive) number of partitions \({\mathcal p}_1,\ldots,{\mathcal p}_n\), of \(r\), there is a grid partition \(\mathcal g\) of \(r\) which is a refinement of. We say that $p'$ is a refinement of $p$ if $p'$ $\supseteq$ $p$. Ø refinement of a partition let p and p * be two partitions of an interval [ ab , ] such that pp ì * i.e. A refinement of the partition p is another partition p' that contains all the points from p and some additional points, again sorted by order of magnitude. Let $p$, $p'$ be partitions at $[a,b]$. Suppose that two partitions $p(x, t)$ and $q(y, s)$ are both partitions of the interval $[a, b]$. Upper and lower sums of different partitions¶ if we take any two partitions of $[a,b]$, say $p_1$ and $p_2$, then we can combine their numbers to make a partition that is a refinement of both.