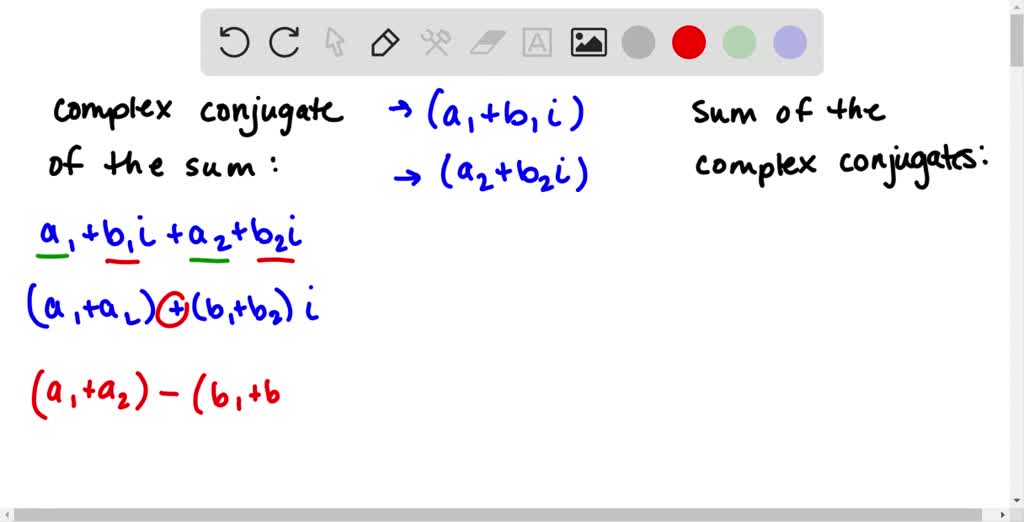
Is The Set Of Complex Numbers A Field . We will now verify that the set of complex numbers is also a. The field of complex numbers. The set of complex numbers is a field. C c is the set of all complex numbers. I have found out that the additive identity is. Recall that the set of real numbers is a field. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. Consider the algebraic structure (c, +, ×) (c, +, ×), where: + + is the operation of complex. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$.
from www.numerade.com
Consider the algebraic structure (c, +, ×) (c, +, ×), where: We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? C c is the set of all complex numbers. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. The set of complex numbers is a field. + + is the operation of complex. The field of complex numbers. I have found out that the additive identity is. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$.
SOLVED Draw the following sets of complex numbers in the complex plane
Is The Set Of Complex Numbers A Field I have found out that the additive identity is. + + is the operation of complex. C c is the set of all complex numbers. The field of complex numbers. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. I have found out that the additive identity is. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. The set of complex numbers is a field. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. Consider the algebraic structure (c, +, ×) (c, +, ×), where: Recall that the set of real numbers is a field. We will now verify that the set of complex numbers is also a.
From www.slideserve.com
PPT Introduction to Complex Numbers PowerPoint Presentation, free Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers is also a. Recall that the set of real numbers is a field. We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. + + is the operation of complex. I have found out that the additive identity is. Consider the. Is The Set Of Complex Numbers A Field.
From www.pinterest.com
Creating a Number Set Venn Diagram Poster Venn diagram, Math methods Is The Set Of Complex Numbers A Field I have found out that the additive identity is. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? We will now verify that the set of complex numbers is also a. + + is the operation of complex. We will now verify that the set. Is The Set Of Complex Numbers A Field.
From www.ck12.org
Imaginary and Complex Numbers CK12 Foundation Is The Set Of Complex Numbers A Field Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? Consider the algebraic structure (c, +, ×) (c, +, ×), where: The field of complex numbers. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$.. Is The Set Of Complex Numbers A Field.
From www.youtube.com
2.5 Complex Numbers and Roots YouTube Is The Set Of Complex Numbers A Field C c is the set of all complex numbers. + + is the operation of complex. We will now verify that the set of complex numbers is also a. Consider the algebraic structure (c, +, ×) (c, +, ×), where: The set of complex numbers is a field. I have found out that the additive identity is. Recall that the. Is The Set Of Complex Numbers A Field.
From owlcation.com
Math How to Use Complex Numbers and the Complex Plane Owlcation Is The Set Of Complex Numbers A Field I have found out that the additive identity is. The field of complex numbers. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? We will. Is The Set Of Complex Numbers A Field.
From quizlet.com
Plot each set of complex numbers in a complex plane. A = 4 Quizlet Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. + + is the operation of complex. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? I have found out that the additive identity is. The. Is The Set Of Complex Numbers A Field.
From www.youtube.com
Complex numbers Solving Equations (with example) YouTube Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers is also a. The field of complex numbers. Consider the algebraic structure (c, +, ×) (c, +, ×), where: I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. Do the field of complex numbers arise necessarily and uniquely as. Is The Set Of Complex Numbers A Field.
From www.slideserve.com
PPT Complex Numbers PowerPoint Presentation, free download ID478903 Is The Set Of Complex Numbers A Field + + is the operation of complex. We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. We will now verify that the set of complex numbers is also a. I. Is The Set Of Complex Numbers A Field.
From www.chegg.com
Solved Let C be the field of complex numbers and R the Is The Set Of Complex Numbers A Field C c is the set of all complex numbers. We will now verify that the set of complex numbers is also a. Recall that the set of real numbers is a field. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. We will now verify that the set of. Is The Set Of Complex Numbers A Field.
From www.radfordmathematics.com
Complex Numbers Radford Mathematics Is The Set Of Complex Numbers A Field The field of complex numbers. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? The set of complex numbers is a field. We will now verify that the set of complex numbers is also a. + + is the operation of complex. I have found. Is The Set Of Complex Numbers A Field.
From www.numerade.com
SOLVED Draw the following sets of complex numbers in the complex plane Is The Set Of Complex Numbers A Field C c is the set of all complex numbers. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. Recall that the set of real numbers is a field. I have found out that the additive identity is. Do the field of complex numbers arise necessarily and uniquely as the. Is The Set Of Complex Numbers A Field.
From www.youtube.com
Learn the Number Sets to better understand math jensenmath.ca YouTube Is The Set Of Complex Numbers A Field Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? The field of complex numbers. Recall that the set of real numbers is a field. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and. Is The Set Of Complex Numbers A Field.
From www.slideshare.net
Complex numbers 1 Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. Recall that the set of real numbers is a field. C c is the set of all complex numbers. The set of complex numbers is a field. Consider the algebraic structure (c, +, ×) (c, +, ×), where: The field of. Is The Set Of Complex Numbers A Field.
From www.youtube.com
Complex Numbers Definition and Vector Form YouTube Is The Set Of Complex Numbers A Field I have found out that the additive identity is. Recall that the set of real numbers is a field. We will now verify that the set of complex numbers is also a. C c is the set of all complex numbers. The field of complex numbers. The set of complex numbers is a field. + + is the operation of. Is The Set Of Complex Numbers A Field.
From www.ck12.org
Defining Complex Numbers ( Read ) Trigonometry CK12 Foundation Is The Set Of Complex Numbers A Field I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. C c is the set of all complex numbers. Consider the algebraic structure (c, +, ×) (c, +, ×), where: I have found out that the additive identity is. + + is the operation of complex. Recall that the set. Is The Set Of Complex Numbers A Field.
From thinkzone.wlonk.com
Number Sets Is The Set Of Complex Numbers A Field The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. We will now verify that the set of complex numbers is also a. C c is the set of. Is The Set Of Complex Numbers A Field.
From www.cuemath.com
Complex Number Formula Learn Formulas for Complex Number Is The Set Of Complex Numbers A Field The field of complex numbers. We will now verify that the set of complex numbers is also a. Recall that the set of real numbers is a field. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. I would like to know how to prove that $\mathbb. Is The Set Of Complex Numbers A Field.
From mrtolaralgebra2.blogspot.com
Algebra 2 2.3a Complex Numbers Is The Set Of Complex Numbers A Field C c is the set of all complex numbers. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. We will now verify that the set of complex numbers is also a. The set of complex numbers is a field. I would like to know how to prove. Is The Set Of Complex Numbers A Field.
From saylordotorg.github.io
Complex Numbers and Their Operations Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. The field of complex numbers. Consider the algebraic structure (c, +, ×) (c, +, ×), where: We will now. Is The Set Of Complex Numbers A Field.
From www.youtube.com
Lesson 5 Factoring Over the Complex Numbers YouTube Is The Set Of Complex Numbers A Field The field of complex numbers. Recall that the set of real numbers is a field. The set of complex numbers is a field. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. I would like to know how to prove that $\mathbb c$ is a field, $. Is The Set Of Complex Numbers A Field.
From mathsathome.com
How to Use De Moivre’s Theorem to Find Powers of Complex Numbers Is The Set Of Complex Numbers A Field C c is the set of all complex numbers. The set of complex numbers is a field. + + is the operation of complex. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. Consider the algebraic structure (c, +, ×) (c, +, ×), where: I would like. Is The Set Of Complex Numbers A Field.
From www.studypool.com
SOLUTION Complex numbers handwritten notes Studypool Is The Set Of Complex Numbers A Field C c is the set of all complex numbers. + + is the operation of complex. Consider the algebraic structure (c, +, ×) (c, +, ×), where: I have found out that the additive identity is. Recall that the set of real numbers is a field. Do the field of complex numbers arise necessarily and uniquely as the only field. Is The Set Of Complex Numbers A Field.
From www.aplustopper.com
Complex Numbers A Plus Topper Is The Set Of Complex Numbers A Field C c is the set of all complex numbers. We will now verify that the set of complex numbers is also a. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. Consider the algebraic structure (c, +, ×) (c, +, ×), where: + + is the operation of complex.. Is The Set Of Complex Numbers A Field.
From quickmath.com
Basics of complex number StepbyStep Math Problem Solver Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers is also a. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. The set of complex numbers is a field. The field of complex numbers. I have found out that the additive identity is. The field of complex numbers. Is The Set Of Complex Numbers A Field.
From ncvm4.books.nba.co.za
Complex Numbers Working with complex numbers National Curriculum Is The Set Of Complex Numbers A Field Recall that the set of real numbers is a field. We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. C c is the set of all complex numbers. Consider the algebraic structure (c, +, ×) (c, +, ×), where: The field of complex numbers (c, +, ×) is the set. Is The Set Of Complex Numbers A Field.
From mathsathome.com
How to Find the Modulus and Argument of a Complex Number Is The Set Of Complex Numbers A Field + + is the operation of complex. I have found out that the additive identity is. The set of complex numbers is a field. We will now verify that the set of complex numbers is also a. The field of complex numbers. We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of. Is The Set Of Complex Numbers A Field.
From www.aakash.ac.in
Complex Numbers Definition, Properties & Geometrical Representation AESL Is The Set Of Complex Numbers A Field The set of complex numbers is a field. The field of complex numbers. C c is the set of all complex numbers. Consider the algebraic structure (c, +, ×) (c, +, ×), where: I have found out that the additive identity is. We will now verify that the set of complex numbers is also a. + + is the operation. Is The Set Of Complex Numbers A Field.
From www.youtube.com
Introduction to Complex Numbers YouTube Is The Set Of Complex Numbers A Field The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered. Is The Set Of Complex Numbers A Field.
From www.youtube.com
Ordered Pair form of Complex Numbers YouTube Is The Set Of Complex Numbers A Field Consider the algebraic structure (c, +, ×) (c, +, ×), where: I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. I have found out that the additive identity is. C c is the set of all complex numbers. The field of complex numbers. Do the field of complex numbers. Is The Set Of Complex Numbers A Field.
From www.wizeprep.com
Basics of Complex Numbers Wize University Linear Algebra Textbook Is The Set Of Complex Numbers A Field Do the field of complex numbers arise necessarily and uniquely as the only field of pairs of ordered real numbers retaining some desired proprieties? The field of complex numbers. + + is the operation of complex. I have found out that the additive identity is. The field of complex numbers (c, +, ×) is the set of complex numbers under. Is The Set Of Complex Numbers A Field.
From antapex.org
Albert van der Sel Complex numbers. Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. The field of complex numbers. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. Consider the algebraic structure (c, +, ×) (c, +, ×), where: + + is. Is The Set Of Complex Numbers A Field.
From www.nagwa.com
Question Video Solving Quadratic Equations over the Set of Complex Is The Set Of Complex Numbers A Field The field of complex numbers. I have found out that the additive identity is. Recall that the set of real numbers is a field. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb c, +, \times)$. + + is the operation of complex. We will now verify that the set of complex. Is The Set Of Complex Numbers A Field.
From chalkdustmagazine.com
Complex numbers and algebra Chalkdust Is The Set Of Complex Numbers A Field We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. + + is the operation of complex. C c is the set of all complex numbers. The set of complex numbers is a field. I would like to know how to prove that $\mathbb c$ is a field, $ ( \mathbb. Is The Set Of Complex Numbers A Field.
From www.youtube.com
05 The Field of Complex Numbers YouTube Is The Set Of Complex Numbers A Field Consider the algebraic structure (c, +, ×) (c, +, ×), where: We will now verify that the set of complex numbers is also a. The field of complex numbers (c, +, ×) is the set of complex numbers under the two operations of addition and multiplication. Do the field of complex numbers arise necessarily and uniquely as the only field. Is The Set Of Complex Numbers A Field.
From www.youtube.com
Complex numbers with examples Introduction YouTube Is The Set Of Complex Numbers A Field The field of complex numbers. C c is the set of all complex numbers. We will now verify that the set of complex numbers $\mathbb{c}$ forms a field under the operations of addition. Consider the algebraic structure (c, +, ×) (c, +, ×), where: The field of complex numbers (c, +, ×) is the set of complex numbers under the. Is The Set Of Complex Numbers A Field.