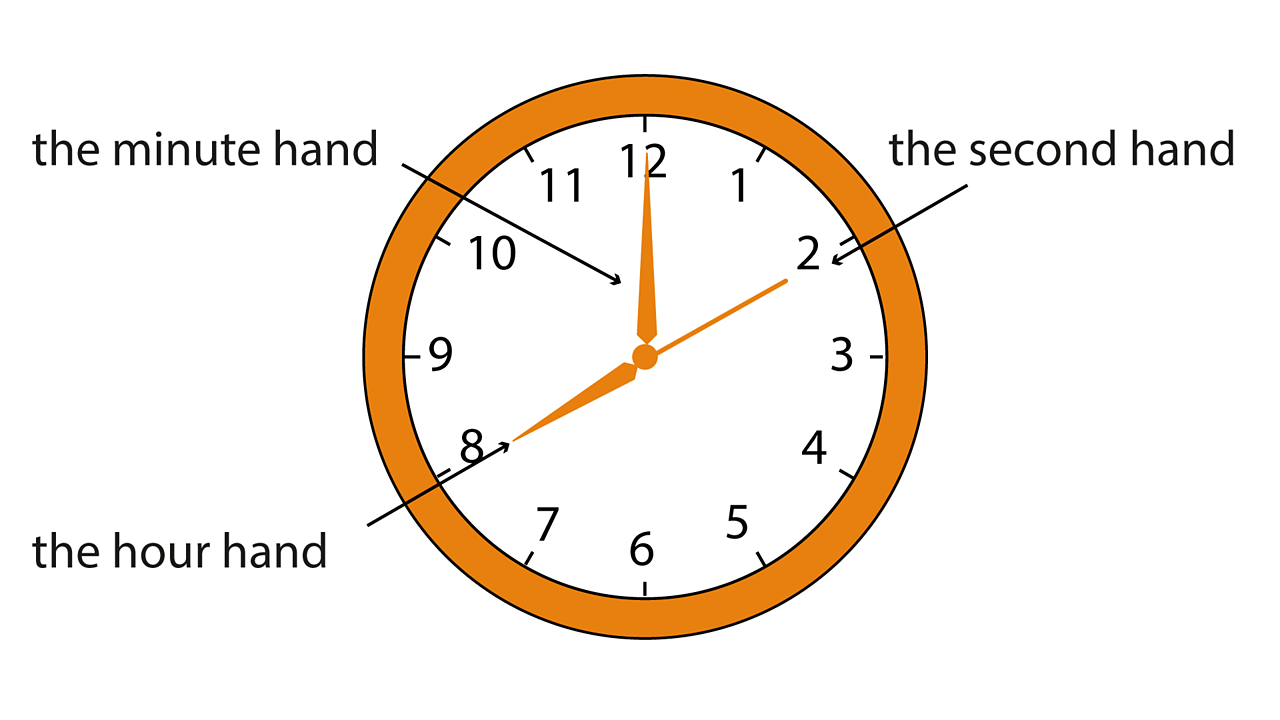
How Many Times Does A Clock's Hands Overlap In 24 Hours . This may seem surprising, as one might expect the hands to overlap 24 times since. 22 times a day if you only count the minute and hour hands overlapping. the second, minute and hour hands are all parallel four times in 24 hours: so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. The hands only then overlap at. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times.
from www.bbc.co.uk
the second, minute and hour hands are all parallel four times in 24 hours: so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. 22 times a day if you only count the minute and hour hands overlapping. The hands only then overlap at. This may seem surprising, as one might expect the hands to overlap 24 times since. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at.
Hours and days Maths Learning with BBC Bitesize BBC Bitesize
How Many Times Does A Clock's Hands Overlap In 24 Hours so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. the second, minute and hour hands are all parallel four times in 24 hours: so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. 22 times a day if you only count the minute and hour hands overlapping. This may seem surprising, as one might expect the hands to overlap 24 times since. The hands only then overlap at.
From quizandriddles.com
How many times do the hands of a clock overlap in a day? Daily Quiz How Many Times Does A Clock's Hands Overlap In 24 Hours Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. the second, minute and hour hands are all parallel four times in 24 hours: as the minute hand approaches the hour hand, the hour hand advances to the. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From interestingengineering.com
Have You Ever Wondered How Many Times a Clock's Hands Overlap in a Day? How Many Times Does A Clock's Hands Overlap In 24 Hours as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. This may seem surprising, as one might expect the hands to overlap 24 times since. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From finwise.edu.vn
Top 94+ Pictures How Many Times Do Clock Hands Overlap Updated How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From infinitesimallysmall.com
When Do A Clock’s Hands Overlap? The Other Side Of Mathematics How Many Times Does A Clock's Hands Overlap In 24 Hours This may seem surprising, as one might expect the hands to overlap 24 times since. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. 22 times a day if you only count the minute and hour hands overlapping. as the minute hand approaches. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Does A Clock's Hands Overlap In 24 Hours Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. The hands only then overlap at. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. as the minute hand approaches the hour hand,. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.livecareer.com
Times Clock Hands Overlap? Interview Questions LiveCareer How Many Times Does A Clock's Hands Overlap In 24 Hours the second, minute and hour hands are all parallel four times in 24 hours: Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. so the hands match up every $65 \frac 5{11} $ minutes and this occurs. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From militaryalphabet.net
Military Time How to convert 24 hour clock How Many Times Does A Clock's Hands Overlap In 24 Hours Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. 22 times a day if you only count the minute and hour hands overlapping. the second, minute and hour hands are all parallel four times in 24 hours: . How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.youtube.com
How Many Times Are A Clock's Hands Opposite During a 24 Hour Day Step How Many Times Does A Clock's Hands Overlap In 24 Hours so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. 22 times a day if you only count the minute and hour hands overlapping. The hands only then overlap at. as the minute hand approaches the hour hand, the hour hand advances to the. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.youtube.com
How Many Times do a Clock's Hands Make a 30 Degree Angle During a 24 How Many Times Does A Clock's Hands Overlap In 24 Hours as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. 22 times a day if you only count the minute and hour hands overlapping. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. Once when they. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.youtube.com
How Many Times are the Clock's Hands at Right Angles During a 24 Hour How Many Times Does A Clock's Hands Overlap In 24 Hours This may seem surprising, as one might expect the hands to overlap 24 times since. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. Time overlap occurs at 24:00:00 (since we count starting as one of. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.toppr.com
The number of times the minute and hour hands of a clock overlap in 24 How Many Times Does A Clock's Hands Overlap In 24 Hours The hands only then overlap at. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. 22 times a day if you only count the minute and hour hands overlapping. This may seem surprising, as one might. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.youtube.com
Interview puzzles with answersHow many times do all hands of clock How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. This may seem surprising, as one might expect the hands to overlap 24 times since. The hands only then overlap at. the second, minute and hour hands are all parallel four times in 24 hours: Time overlap occurs at 24:00:00 (since we count starting as. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From pickedwatch.com
How to Read a Clock with Hands The Most Simple Guide How Many Times Does A Clock's Hands Overlap In 24 Hours Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. This may seem surprising, as one might expect the hands to overlap 24 times since. Time overlap occurs at 24:00:00. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From exowiedny.blob.core.windows.net
How Many Hands In Clock at Bruce Perry blog How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. the second, minute and hour hands are all parallel four times in 24 hours: Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. . How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.youtube.com
How Many Times do a Clock's Hands Make a 45 Degree Angle During a 24 How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. This may seem surprising, as one might expect the hands to overlap 24 times since. the second, minute and hour hands are all parallel four times in 24 hours: so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From et.mathigon.org
Overlapping Hands of a Clock Mathigon How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. The hands only then overlap at. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. as the minute hand approaches the hour hand, the hour hand advances to the. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.bbc.co.uk
Hours and days Maths Learning with BBC Bitesize BBC Bitesize How Many Times Does A Clock's Hands Overlap In 24 Hours so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. This may seem surprising, as one might expect the hands to overlap 24 times since. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. The hands. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.geeksforgeeks.org
Distance between end points of Hour and minute hand at given time How Many Times Does A Clock's Hands Overlap In 24 Hours This may seem surprising, as one might expect the hands to overlap 24 times since. the second, minute and hour hands are all parallel four times in 24 hours: 22 times a day if you only count the minute and hour hands overlapping. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From finwise.edu.vn
Top 94+ Pictures How Many Times Do Clock Hands Overlap Updated How Many Times Does A Clock's Hands Overlap In 24 Hours Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. This may seem surprising, as one might expect the hands to overlap 24 times since. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. 22 times a day if you only count the minute and hour. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From karakais.blogspot.com
Kais's blog How many times do a clock's hands overlap in a day How Many Times Does A Clock's Hands Overlap In 24 Hours as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. 22 times a day if you only count the minute and hour hands overlapping. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. The hands only then overlap at. the second, minute and hour hands. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From brainly.com
At noon, the minute and the hour hands of a clock overlap. In how long How Many Times Does A Clock's Hands Overlap In 24 Hours as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. The hands only then overlap at. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. the second, minute and hour. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From finwise.edu.vn
Top 94+ Pictures How Many Times Do Clock Hands Overlap Updated How Many Times Does A Clock's Hands Overlap In 24 Hours the second, minute and hour hands are all parallel four times in 24 hours: Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. The hands only then overlap. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.youtube.com
How Many Times do hands of clock coincide in a dayMaths trick for How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. This may seem surprising, as one might expect the hands to overlap 24 times since. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps,. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Does A Clock's Hands Overlap In 24 Hours so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. The hands only then overlap. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. the second, minute and hour hands are all parallel four times in 24 hours: This may seem surprising, as one might expect the hands to overlap 24 times since. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. The. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From math.stackexchange.com
geometry How many times are the hands of a clock at 90 degrees How Many Times Does A Clock's Hands Overlap In 24 Hours as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. the second, minute and hour hands are all parallel four times in 24 hours: so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. 22 times. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.splashlearn.com
What is Time? Definition, Uses, Conversion, Measurement, Example How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. This may seem surprising, as one might expect the hands to overlap 24 times since. The hands only then overlap at. the second, minute and hour hands. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From laughingsquid.com
How Many Times the Hands of an Analogue Clock Overlap With Each Other How Many Times Does A Clock's Hands Overlap In 24 Hours so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. The hands only then overlap. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From twitter.com
🇺🇦Evan Kirstel B2B TechFluencer on Twitter "🤔 ⏰ How many times a day How Many Times Does A Clock's Hands Overlap In 24 Hours Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. as the minute hand approaches the hour hand, the hour hand advances to the. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From exowiedny.blob.core.windows.net
How Many Hands In Clock at Bruce Perry blog How Many Times Does A Clock's Hands Overlap In 24 Hours Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. so the hands match up every $65 \frac 5{11} $ minutes and this occurs. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From watchrevealer.com
How Many Times a Day Minute And Hour Hand Overlap? Watch Revealer How Many Times Does A Clock's Hands Overlap In 24 Hours 22 times a day if you only count the minute and hour hands overlapping. the second, minute and hour hands are all parallel four times in 24 hours: The hands only then overlap at. This may seem surprising, as one might expect the hands to overlap 24 times since. as the minute hand approaches the hour hand, the. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From cecmvtuj.blob.core.windows.net
What Is 333 Minutes In Hours at Lawrence Maskell blog How Many Times Does A Clock's Hands Overlap In 24 Hours This may seem surprising, as one might expect the hands to overlap 24 times since. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. as the minute hand approaches the hour hand, the hour hand advances to the. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From exosnwhyu.blob.core.windows.net
How Many Times Do A Clock S Hands Overlap Each Day at Jill Baker blog How Many Times Does A Clock's Hands Overlap In 24 Hours so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. 22 times a day if you only count the minute and hour hands overlapping. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From www.youtube.com
HOW MANY TIMES IN A DAY,ARE THE HANDS OF A CLOCK IN STRAIGHT LINE BUT How Many Times Does A Clock's Hands Overlap In 24 Hours Once when they are aligned at midnight, twice at 06:00 and 12:00:00, and once at. Time overlap occurs at 24:00:00 (since we count starting as one of overlaps, this might be excluded) as a result, if you count the last case, there are 23 times. The hands only then overlap at. 22 times a day if you only count the. How Many Times Does A Clock's Hands Overlap In 24 Hours.
From finwise.edu.vn
Top 94+ Pictures How Many Times Do Clock Hands Overlap Updated How Many Times Does A Clock's Hands Overlap In 24 Hours as the minute hand approaches the hour hand, the hour hand advances to the 12 hour mark. 22 times a day if you only count the minute and hour hands overlapping. so the hands match up every $65 \frac 5{11} $ minutes and this occurs $12$ times is a $12$ hour period if you consider. Once when they. How Many Times Does A Clock's Hands Overlap In 24 Hours.