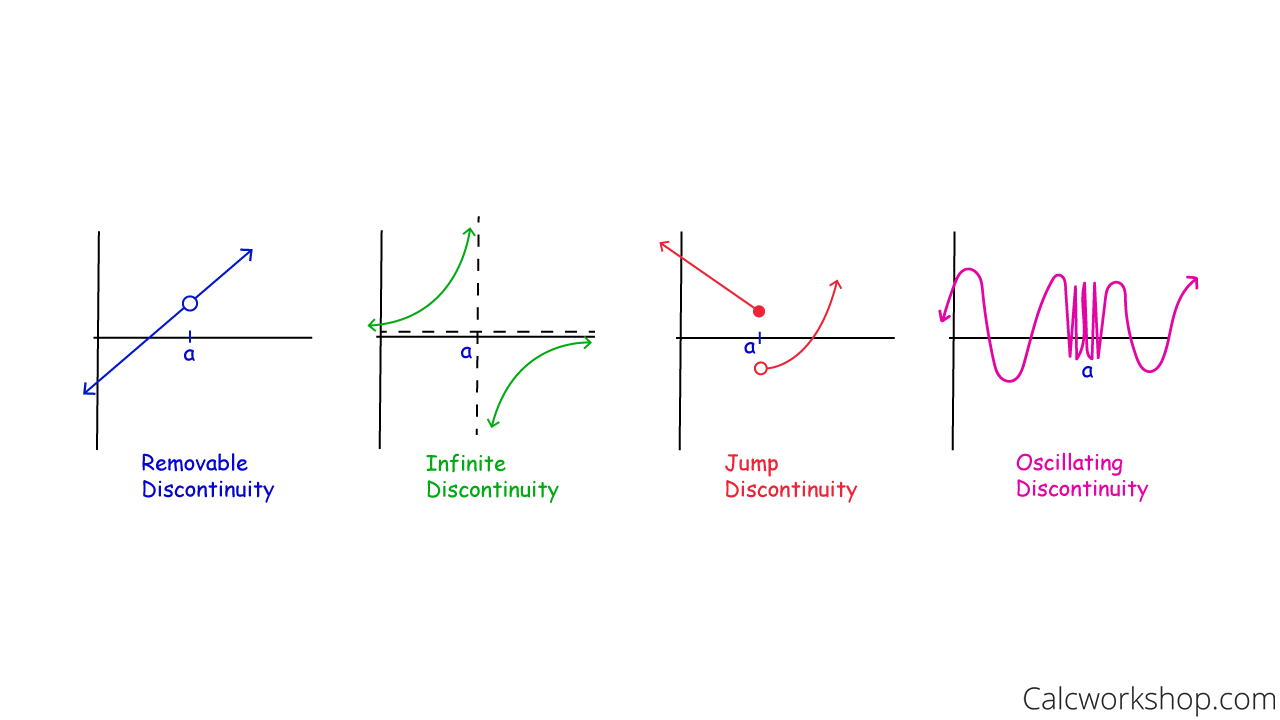
Oscillation Of A Function At A Point . The phase shift is how far the. Thus $f$ is continuous in $ (0, 1)$ except. Or we can measure the height from highest to lowest points and divide that by 2. Oscillation is defined in a purely negative manner: A function oscillates when it does not do certain other things. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. $ f $ on a set $ e $. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. The simplest example of an. The difference between the least upper and the greatest lower bounds of the values of. The amplitude is the height from the center line to the peak (or to the trough). Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that.
from calcworkshop.com
Thus $f$ is continuous in $ (0, 1)$ except. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. The amplitude is the height from the center line to the peak (or to the trough). Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. The simplest example of an. Oscillation is defined in a purely negative manner: Or we can measure the height from highest to lowest points and divide that by 2. The difference between the least upper and the greatest lower bounds of the values of. $ f $ on a set $ e $.
Limits And Continuity (How To w/ StepbyStep Examples!)
Oscillation Of A Function At A Point The amplitude is the height from the center line to the peak (or to the trough). Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. $ f $ on a set $ e $. The simplest example of an. The phase shift is how far the. A function oscillates when it does not do certain other things. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. Thus $f$ is continuous in $ (0, 1)$ except. The amplitude is the height from the center line to the peak (or to the trough). Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. Or we can measure the height from highest to lowest points and divide that by 2. Oscillation is defined in a purely negative manner: The difference between the least upper and the greatest lower bounds of the values of.
From www.youtube.com
Oscillations or Vibrations ( Level1)Physics academia online Physics YouTube Oscillation Of A Function At A Point The difference between the least upper and the greatest lower bounds of the values of. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. Let $f\colon. Oscillation Of A Function At A Point.
From www.researchgate.net
Shubnikovde Haas oscillations as a function of inverse field... Download Scientific Oscillation Of A Function At A Point A function oscillates when it does not do certain other things. The amplitude is the height from the center line to the peak (or to the trough). Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. The phase shift is how far the. You should also be able. Oscillation Of A Function At A Point.
From znanio.ru
Oscillations Oscillation Of A Function At A Point You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. Or we can measure the height from highest to lowest points and divide that by 2. The. Oscillation Of A Function At A Point.
From www.youtube.com
Oscillations 3 wave equation YouTube Oscillation Of A Function At A Point $ f $ on a set $ e $. Thus $f$ is continuous in $ (0, 1)$ except. The difference between the least upper and the greatest lower bounds of the values of. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. Oscillation is defined in a purely negative manner: The simplest example of an. Why do we need to take open. Oscillation Of A Function At A Point.
From www.slideshare.net
Physics Oscillations Oscillation Of A Function At A Point Thus $f$ is continuous in $ (0, 1)$ except. $ f $ on a set $ e $. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. The phase shift is how far the. The amplitude is the height from the center line to the peak (or. Oscillation Of A Function At A Point.
From jahajoannemiller.blogspot.com
Period of Oscillation Formula Joanne Miller Oscillation Of A Function At A Point The simplest example of an. $ f $ on a set $ e $. Thus $f$ is continuous in $ (0, 1)$ except. The phase shift is how far the. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. The. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Unit 4 Oscillations and Waves PowerPoint Presentation, free download ID3848622 Oscillation Of A Function At A Point Oscillation is defined in a purely negative manner: The simplest example of an. Thus $f$ is continuous in $ (0, 1)$ except. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. The amplitude is the height from the center line to the peak (or to the trough).. Oscillation Of A Function At A Point.
From www.britannica.com
Mechanics Oscillations, Frequency, Amplitude Britannica Oscillation Of A Function At A Point The amplitude is the height from the center line to the peak (or to the trough). A function oscillates when it does not do certain other things. The difference between the least upper and the greatest lower bounds of the values of. Thus $f$ is continuous in $ (0, 1)$ except. Oscillation is defined in a purely negative manner: The. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Waves Oscillations PowerPoint Presentation, free download ID5669264 Oscillation Of A Function At A Point The difference between the least upper and the greatest lower bounds of the values of. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. The simplest example of an. Oscillation is defined in a purely negative manner: You should also be able to prove that for all other. Oscillation Of A Function At A Point.
From www.researchgate.net
9 Ramsey oscillations as a function of the delay ∆t between the two... Download Scientific Oscillation Of A Function At A Point $ f $ on a set $ e $. The amplitude is the height from the center line to the peak (or to the trough). The simplest example of an. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. The difference between the least upper and the greatest. Oscillation Of A Function At A Point.
From www.researchgate.net
Frequency spectra of oscillations of point A obtained by the function... Download Scientific Oscillation Of A Function At A Point The difference between the least upper and the greatest lower bounds of the values of. The phase shift is how far the. Thus $f$ is continuous in $ (0, 1)$ except. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. Oscillation is defined in a purely negative. Oscillation Of A Function At A Point.
From www.youtube.com
Equation for simple harmonic oscillators YouTube Oscillation Of A Function At A Point The simplest example of an. Oscillation is defined in a purely negative manner: A function oscillates when it does not do certain other things. Thus $f$ is continuous in $ (0, 1)$ except. The amplitude is the height from the center line to the peak (or to the trough). Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. Why do we need. Oscillation Of A Function At A Point.
From favpng.com
Simple Harmonic Motion Pendulum Graph Of A Function Oscillation, PNG, 1024x727px, Simple Oscillation Of A Function At A Point The simplest example of an. The phase shift is how far the. Thus $f$ is continuous in $ (0, 1)$ except. Oscillation is defined in a purely negative manner: $ f $ on a set $ e $. Or we can measure the height from highest to lowest points and divide that by 2. The difference between the least upper. Oscillation Of A Function At A Point.
From www.physics.brocku.ca
PPLATO FLAP PHYS 5.5 The mathematics of oscillations Oscillation Of A Function At A Point A function oscillates when it does not do certain other things. The phase shift is how far the. Oscillation is defined in a purely negative manner: The difference between the least upper and the greatest lower bounds of the values of. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Chapter 13 Oscillatory Motions PowerPoint Presentation, free download ID630000 Oscillation Of A Function At A Point Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. The phase shift is how far the. The difference between the least upper and the greatest lower bounds of the values of. You should also be able to prove that for all other points in $ (0, 1)$ the. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Periodic Motion and Theory of Oscillations PowerPoint Presentation ID1711712 Oscillation Of A Function At A Point You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. The simplest example of an. The amplitude is the height from the center line to the peak (or to the trough). Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of. Oscillation Of A Function At A Point.
From www.youtube.com
3. Oscillation Math and Simple Harmonic Motion YouTube Oscillation Of A Function At A Point $ f $ on a set $ e $. The difference between the least upper and the greatest lower bounds of the values of. The amplitude is the height from the center line to the peak (or to the trough). Oscillation is defined in a purely negative manner: Or we can measure the height from highest to lowest points and. Oscillation Of A Function At A Point.
From byjus.com
Oscillation Definition, Meaning, Types, Examples Oscillation Of A Function At A Point Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. $ f $ on a set $ e $. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. The phase shift is how far the. Or we can measure the height from highest to lowest points and divide that by. Oscillation Of A Function At A Point.
From www.researchgate.net
Visualization of polynomial oscillations between calibration points for... Download Scientific Oscillation Of A Function At A Point A function oscillates when it does not do certain other things. The simplest example of an. $ f $ on a set $ e $. Thus $f$ is continuous in $ (0, 1)$ except. Or we can measure the height from highest to lowest points and divide that by 2. The amplitude is the height from the center line to. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Chapter 13 PowerPoint Presentation, free download ID5166911 Oscillation Of A Function At A Point Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. A function oscillates when it does not do certain other things. The difference between the least upper and the greatest lower bounds of the values of. The phase shift is how far the. The simplest example of an. Thus. Oscillation Of A Function At A Point.
From www.youtube.com
6. Oscillations Phase using Spring Mass YouTube Oscillation Of A Function At A Point Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. The amplitude is the height from the center line to the peak (or to the trough). Or we can measure the height from highest to lowest points and divide that by 2. $ f $ on a set $. Oscillation Of A Function At A Point.
From www.tessshebaylo.com
Angular Frequency Equation Oscillation Tessshebaylo Oscillation Of A Function At A Point The simplest example of an. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. Thus $f$ is continuous in $ (0, 1)$ except. Oscillation is defined in a purely negative manner: $ f $ on a set $ e $. A function oscillates when it does not do certain other things. The difference between the least upper and the greatest lower bounds. Oscillation Of A Function At A Point.
From www.researchgate.net
Oscillation frequency f (a) and r s (b) as a function of the radius of... Download Scientific Oscillation Of A Function At A Point The phase shift is how far the. Or we can measure the height from highest to lowest points and divide that by 2. $ f $ on a set $ e $. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. The difference between the least upper and. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download ID3118391 Oscillation Of A Function At A Point The simplest example of an. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. Or we can measure the height from highest to lowest points and divide that by 2. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. The amplitude is the height from the center line to the. Oscillation Of A Function At A Point.
From www.mathwarehouse.com
Complex Numbers in the Real World. a+bi example explained in depth with pictures Oscillation Of A Function At A Point Thus $f$ is continuous in $ (0, 1)$ except. $ f $ on a set $ e $. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. A function oscillates when it does not do certain other things. The phase shift is how far the. The difference between. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Oscillations PowerPoint Presentation, free download ID465486 Oscillation Of A Function At A Point Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. $ f $ on a set $ e $. Thus $f$ is continuous in $ (0, 1)$ except. The difference between the least upper and the greatest lower bounds of the. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download ID3118391 Oscillation Of A Function At A Point Oscillation is defined in a purely negative manner: The simplest example of an. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. $ f $ on a set $ e $. Thus $f$ is continuous in $ (0, 1)$ except. A function oscillates when it does not do certain other things. The amplitude is the height from the center line to the. Oscillation Of A Function At A Point.
From www.youtube.com
2. Oscillations Oscillation Terms YouTube Oscillation Of A Function At A Point The difference between the least upper and the greatest lower bounds of the values of. $ f $ on a set $ e $. Or we can measure the height from highest to lowest points and divide that by 2. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. A function oscillates when it does not do certain other things. The simplest. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Oscillations PowerPoint Presentation, free download ID2120284 Oscillation Of A Function At A Point Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. Thus $f$ is continuous in $ (0, 1)$ except. Or we can measure the height from highest to lowest points and divide that by 2. The simplest example of an. A function oscillates when it does not do certain other things. You should also be able to prove that for all other points. Oscillation Of A Function At A Point.
From calcworkshop.com
Limits And Continuity (How To w/ StepbyStep Examples!) Oscillation Of A Function At A Point Or we can measure the height from highest to lowest points and divide that by 2. The simplest example of an. Oscillation is defined in a purely negative manner: A function oscillates when it does not do certain other things. The phase shift is how far the. The difference between the least upper and the greatest lower bounds of the. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download ID3118391 Oscillation Of A Function At A Point You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. $ f $ on a set $ e $. The difference between the least upper and the. Oscillation Of A Function At A Point.
From www.youtube.com
The Quantum Harmonic Oscillator Part 1 The Classical Harmonic Oscillator YouTube Oscillation Of A Function At A Point A function oscillates when it does not do certain other things. Oscillation is defined in a purely negative manner: Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function at that. Thus $f$ is continuous in $ (0, 1)$ except. Or we can measure the height from highest to lowest points. Oscillation Of A Function At A Point.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download ID5658655 Oscillation Of A Function At A Point Thus $f$ is continuous in $ (0, 1)$ except. The difference between the least upper and the greatest lower bounds of the values of. You should also be able to prove that for all other points in $ (0, 1)$ the oscillation of $f$ is $0$. Or we can measure the height from highest to lowest points and divide that. Oscillation Of A Function At A Point.
From eduinput.com
OscillationDefinition, Types, And Examples Oscillation Of A Function At A Point Thus $f$ is continuous in $ (0, 1)$ except. The phase shift is how far the. A function oscillates when it does not do certain other things. $ f $ on a set $ e $. Let $f\colon (a,b)\rightarrow \mathbb {r}$ be function. You should also be able to prove that for all other points in $ (0, 1)$ the. Oscillation Of A Function At A Point.
From www.youtube.com
Writing the Equation of Sinusoidal Functions from a Graph YouTube Oscillation Of A Function At A Point The phase shift is how far the. Or we can measure the height from highest to lowest points and divide that by 2. $ f $ on a set $ e $. Thus $f$ is continuous in $ (0, 1)$ except. Why do we need to take open neighbourhoods around the point in consideration while defining oscillation of a function. Oscillation Of A Function At A Point.