How Many Ways Can 15 Students Be Divided Into Three Groups . This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. If the students are lined up then the order of the. In how many ways can. I think the answer should be $\frac{12!}{(4!)^3}$ but the. In general, n distinct objects can be arranged in \displaystyle {n}! How many ways $12$ persons may be divided into three groups of $4$ persons each? Therefore, the number of ways to arrange students in 3 equal groups is: 5!}$$ but, the labeling of the groups also does not matter. We were asked to figure out how many ways the students can be lined up. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$?
from www.chegg.com
In general, n distinct objects can be arranged in \displaystyle {n}! We were asked to figure out how many ways the students can be lined up. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? I think the answer should be $\frac{12!}{(4!)^3}$ but the. How many ways $12$ persons may be divided into three groups of $4$ persons each? In how many ways can. If the students are lined up then the order of the. This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. Therefore, the number of ways to arrange students in 3 equal groups is: 5!}$$ but, the labeling of the groups also does not matter.
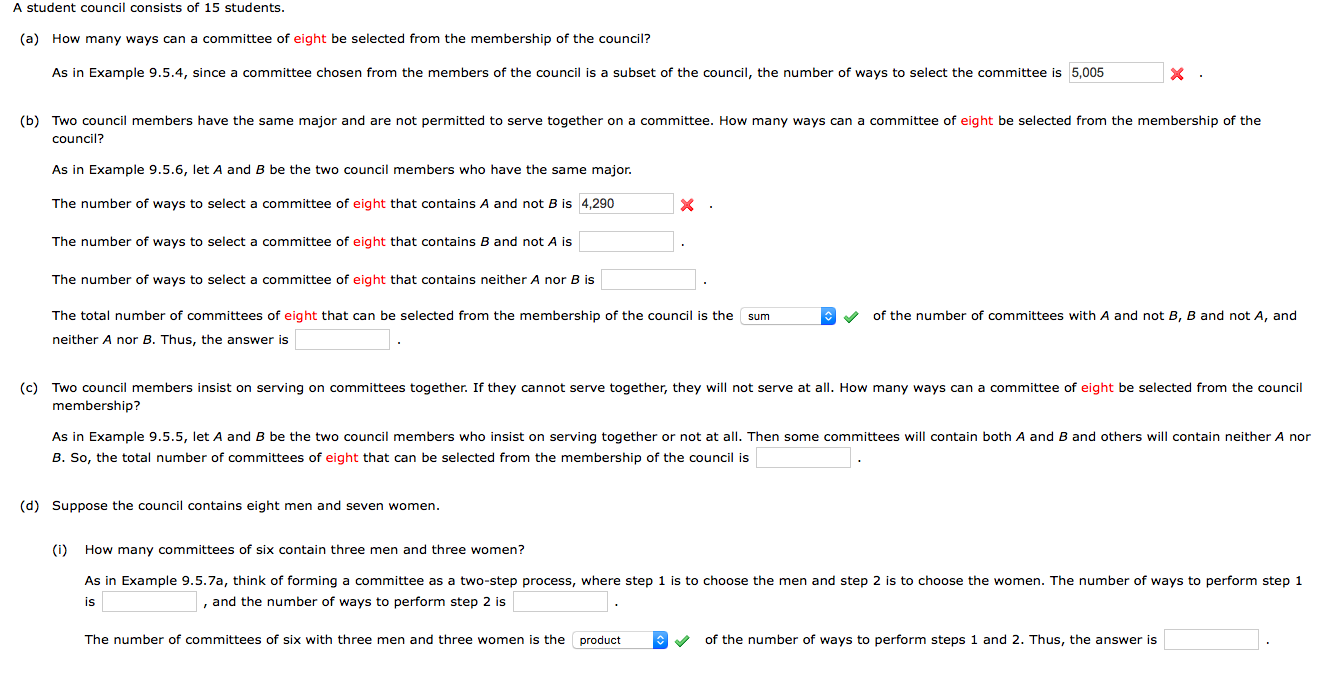
Solved A student council consists of 15 students. (a) How
How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can. In general, n distinct objects can be arranged in \displaystyle {n}! This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. I think the answer should be $\frac{12!}{(4!)^3}$ but the. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? 5!}$$ but, the labeling of the groups also does not matter. If the students are lined up then the order of the. We were asked to figure out how many ways the students can be lined up. Therefore, the number of ways to arrange students in 3 equal groups is: In how many ways can. How many ways $12$ persons may be divided into three groups of $4$ persons each?
From www.slideserve.com
PPT Teaching Strategies and Learning Styles CRAW Feb 23 How Many Ways Can 15 Students Be Divided Into Three Groups Therefore, the number of ways to arrange students in 3 equal groups is: In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? In how many ways can. In general, n distinct objects can be arranged in \displaystyle {n}! We were asked to figure out how many ways. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.slideserve.com
PPT Assignment All students who registered this course will be How Many Ways Can 15 Students Be Divided Into Three Groups I think the answer should be $\frac{12!}{(4!)^3}$ but the. If the students are lined up then the order of the. Therefore, the number of ways to arrange students in 3 equal groups is: In general, n distinct objects can be arranged in \displaystyle {n}! This combination calculator (n choose k calculator) is a tool that helps you not only determine. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.scribd.com
Irregular Verbs Divided Into Groups How Many Ways Can 15 Students Be Divided Into Three Groups I think the answer should be $\frac{12!}{(4!)^3}$ but the. If the students are lined up then the order of the. This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. How many ways $12$ persons may be divided into three groups of $4$ persons each? 5!}$$ but, the. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.nagwa.com
Question Video Interpreting Division as the Number of Items in Each How Many Ways Can 15 Students Be Divided Into Three Groups In general, n distinct objects can be arranged in \displaystyle {n}! I think the answer should be $\frac{12!}{(4!)^3}$ but the. In how many ways can. Therefore, the number of ways to arrange students in 3 equal groups is: If the students are lined up then the order of the. We were asked to figure out how many ways the students. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.scribd.com
Roster of students divided into three groups based on their family How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can. How many ways $12$ persons may be divided into three groups of $4$ persons each? In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? 5!}$$ but, the labeling of the groups also does not matter. If the students are lined up then. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.numerade.com
SOLVED Find how many ways 15 children can be divided into three groups How Many Ways Can 15 Students Be Divided Into Three Groups This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. In how many ways can. I think the answer should be $\frac{12!}{(4!)^3}$ but the. 5!}$$ but, the labeling of the groups also does not matter. Therefore, the number of ways to arrange students in 3 equal groups is:. How Many Ways Can 15 Students Be Divided Into Three Groups.
From stock.adobe.com
Interested preteen pupils divided into small groups, discussing How Many Ways Can 15 Students Be Divided Into Three Groups In general, n distinct objects can be arranged in \displaystyle {n}! Therefore, the number of ways to arrange students in 3 equal groups is: This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. I think the answer should be $\frac{12!}{(4!)^3}$ but the. In how many ways can. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.teachercreated.com
Division Tables Chart TCR7578 Teacher Created Resources How Many Ways Can 15 Students Be Divided Into Three Groups I think the answer should be $\frac{12!}{(4!)^3}$ but the. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? If the students are lined up then the order of the. How many ways $12$ persons may be divided into three groups of $4$ persons each? 5!}$$ but, the. How Many Ways Can 15 Students Be Divided Into Three Groups.
From askfilo.com
In how many ways can 15 students be divided into 3 groups of 5 students e.. How Many Ways Can 15 Students Be Divided Into Three Groups This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. Therefore, the number of ways to arrange students in 3 equal groups is: I think the answer should be $\frac{12!}{(4!)^3}$ but the. In how many ways can. How many ways $12$ persons may be divided into three groups. How Many Ways Can 15 Students Be Divided Into Three Groups.
From klayxajah.blob.core.windows.net
In How Many Ways Can 20 Students Be Grouped Into 3 Groups at Louis Dow blog How Many Ways Can 15 Students Be Divided Into Three Groups I think the answer should be $\frac{12!}{(4!)^3}$ but the. In general, n distinct objects can be arranged in \displaystyle {n}! We were asked to figure out how many ways the students can be lined up. In how many ways can. How many ways $12$ persons may be divided into three groups of $4$ persons each? In how many ways can. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.activesuperstars.co.uk
activesuperstars.co.uk Ways to Divide Groups into a Team How Many Ways Can 15 Students Be Divided Into Three Groups We were asked to figure out how many ways the students can be lined up. 5!}$$ but, the labeling of the groups also does not matter. In how many ways can. If the students are lined up then the order of the. In how many ways can a group of $15$ people be divided into three groups of $3$ and. How Many Ways Can 15 Students Be Divided Into Three Groups.
From klayxajah.blob.core.windows.net
In How Many Ways Can 20 Students Be Grouped Into 3 Groups at Louis Dow blog How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can. If the students are lined up then the order of the. I think the answer should be $\frac{12!}{(4!)^3}$ but the. Therefore, the number of ways to arrange students in 3 equal groups is: We were asked to figure out how many ways the students can be lined up. In general, n distinct objects can be. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.dreamstime.com
Teenage Students Discussing Learning Material in Groups in Classroom How Many Ways Can 15 Students Be Divided Into Three Groups We were asked to figure out how many ways the students can be lined up. 5!}$$ but, the labeling of the groups also does not matter. I think the answer should be $\frac{12!}{(4!)^3}$ but the. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? This combination calculator. How Many Ways Can 15 Students Be Divided Into Three Groups.
From gbu-taganskij.ru
Video Unit Fractions Halves, Thirds And Quarters Nagwa, 48 OFF How Many Ways Can 15 Students Be Divided Into Three Groups I think the answer should be $\frac{12!}{(4!)^3}$ but the. How many ways $12$ persons may be divided into three groups of $4$ persons each? If the students are lined up then the order of the. In general, n distinct objects can be arranged in \displaystyle {n}! In how many ways can a group of $15$ people be divided into three. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.nagwa.com
Lesson Video Dividing into Equal Groups Nagwa How Many Ways Can 15 Students Be Divided Into Three Groups We were asked to figure out how many ways the students can be lined up. In general, n distinct objects can be arranged in \displaystyle {n}! I think the answer should be $\frac{12!}{(4!)^3}$ but the. If the students are lined up then the order of the. How many ways $12$ persons may be divided into three groups of $4$ persons. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.facebook.com
Our group divided into three groups and had amazing experiences How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. How many ways $12$ persons may be divided into three groups of $4$ persons each? In. How Many Ways Can 15 Students Be Divided Into Three Groups.
From printabletemplate.concejomunicipaldechinu.gov.co
Free Printable Division Chart How Many Ways Can 15 Students Be Divided Into Three Groups How many ways $12$ persons may be divided into three groups of $4$ persons each? In general, n distinct objects can be arranged in \displaystyle {n}! If the students are lined up then the order of the. I think the answer should be $\frac{12!}{(4!)^3}$ but the. Therefore, the number of ways to arrange students in 3 equal groups is: We. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.numerade.com
SOLVEDIn how many ways can 12 people be divided into three groups of 4 How Many Ways Can 15 Students Be Divided Into Three Groups Therefore, the number of ways to arrange students in 3 equal groups is: We were asked to figure out how many ways the students can be lined up. In general, n distinct objects can be arranged in \displaystyle {n}! If the students are lined up then the order of the. 5!}$$ but, the labeling of the groups also does not. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.vedantu.com
Division for Grade 2 Definition, Facts & Examples How Many Ways Can 15 Students Be Divided Into Three Groups In general, n distinct objects can be arranged in \displaystyle {n}! If the students are lined up then the order of the. Therefore, the number of ways to arrange students in 3 equal groups is: How many ways $12$ persons may be divided into three groups of $4$ persons each? 5!}$$ but, the labeling of the groups also does not. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.teachoo.com
Example 21 A group consists of 4 girls and 7 boys. In how many How Many Ways Can 15 Students Be Divided Into Three Groups In general, n distinct objects can be arranged in \displaystyle {n}! I think the answer should be $\frac{12!}{(4!)^3}$ but the. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? In how many ways can. 5!}$$ but, the labeling of the groups also does not matter. This combination. How Many Ways Can 15 Students Be Divided Into Three Groups.
From teachablemath.com
Division Remainder and Regrouping TeachableMath How Many Ways Can 15 Students Be Divided Into Three Groups 5!}$$ but, the labeling of the groups also does not matter. Therefore, the number of ways to arrange students in 3 equal groups is: In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? In general, n distinct objects can be arranged in \displaystyle {n}! If the students. How Many Ways Can 15 Students Be Divided Into Three Groups.
From brainly.in
Q 68. In how many ways 12 things can be divided into three groups of 3 How Many Ways Can 15 Students Be Divided Into Three Groups 5!}$$ but, the labeling of the groups also does not matter. We were asked to figure out how many ways the students can be lined up. In how many ways can. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? In general, n distinct objects can be. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.chegg.com
Solved A student council consists of 15 students. (a) How How Many Ways Can 15 Students Be Divided Into Three Groups How many ways $12$ persons may be divided into three groups of $4$ persons each? Therefore, the number of ways to arrange students in 3 equal groups is: 5!}$$ but, the labeling of the groups also does not matter. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.numerade.com
SOLVED In how many ways can 18 different pizza toppings be chosen from How Many Ways Can 15 Students Be Divided Into Three Groups 5!}$$ but, the labeling of the groups also does not matter. I think the answer should be $\frac{12!}{(4!)^3}$ but the. In general, n distinct objects can be arranged in \displaystyle {n}! We were asked to figure out how many ways the students can be lined up. Therefore, the number of ways to arrange students in 3 equal groups is: How. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.chegg.com
Solved A student council consists of 15 students. (a) How How Many Ways Can 15 Students Be Divided Into Three Groups 5!}$$ but, the labeling of the groups also does not matter. I think the answer should be $\frac{12!}{(4!)^3}$ but the. If the students are lined up then the order of the. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? This combination calculator (n choose k calculator). How Many Ways Can 15 Students Be Divided Into Three Groups.
From literacymathideas.blogspot.com
Literacy & Math Ideas Three Ways to Divide Fractions How Many Ways Can 15 Students Be Divided Into Three Groups How many ways $12$ persons may be divided into three groups of $4$ persons each? Therefore, the number of ways to arrange students in 3 equal groups is: This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. In how many ways can a group of $15$ people. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.youtube.com
A club consists of 15 members. In how many ways can the three officers How Many Ways Can 15 Students Be Divided Into Three Groups In general, n distinct objects can be arranged in \displaystyle {n}! In how many ways can. 5!}$$ but, the labeling of the groups also does not matter. Therefore, the number of ways to arrange students in 3 equal groups is: This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.onlinemathlearning.com
Division & Equal Groups Worksheets (Printable, Online) How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. I think the answer should be $\frac{12!}{(4!)^3}$ but the. Therefore, the number of ways to arrange. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.numerade.com
SOLVED In how many ways can 8 people be divided into two groups, one How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? I think the answer should be $\frac{12!}{(4!)^3}$ but the. 5!}$$ but, the labeling of the groups also does not matter. Therefore, the number of ways to arrange students in 3 equal groups is: In how many ways can.. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.youtube.com
A Fun Way To Divide Large Groups Into Teams YouTube How Many Ways Can 15 Students Be Divided Into Three Groups Therefore, the number of ways to arrange students in 3 equal groups is: If the students are lined up then the order of the. In how many ways can. 5!}$$ but, the labeling of the groups also does not matter. This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.chegg.com
Solved A student council consists of 15 students. (a) In how How Many Ways Can 15 Students Be Divided Into Three Groups Therefore, the number of ways to arrange students in 3 equal groups is: In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? 5!}$$ but, the labeling of the groups also does not matter. How many ways $12$ persons may be divided into three groups of $4$ persons. How Many Ways Can 15 Students Be Divided Into Three Groups.
From printablelibmulheim.z21.web.core.windows.net
Division As Equal Grouping How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can. We were asked to figure out how many ways the students can be lined up. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? How many ways $12$ persons may be divided into three groups of $4$ persons each? I think the. How Many Ways Can 15 Students Be Divided Into Three Groups.
From mathisvisual.com
Visualizing Whole Number Quotative Division and Partitive Division How Many Ways Can 15 Students Be Divided Into Three Groups How many ways $12$ persons may be divided into three groups of $4$ persons each? In how many ways can. I think the answer should be $\frac{12!}{(4!)^3}$ but the. This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a. If the students are lined up then the order. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.learningprintable.com
division table for kids Learning Printable How Many Ways Can 15 Students Be Divided Into Three Groups In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? 5!}$$ but, the labeling of the groups also does not matter. In how many ways can. Therefore, the number of ways to arrange students in 3 equal groups is: How many ways $12$ persons may be divided into. How Many Ways Can 15 Students Be Divided Into Three Groups.
From www.learningprintable.com
Division Table 112 Learning Printable How Many Ways Can 15 Students Be Divided Into Three Groups In general, n distinct objects can be arranged in \displaystyle {n}! We were asked to figure out how many ways the students can be lined up. In how many ways can a group of $15$ people be divided into three groups of $3$ and three groups of $2$? Therefore, the number of ways to arrange students in 3 equal groups. How Many Ways Can 15 Students Be Divided Into Three Groups.