Expected Number Of Trials Until Success . This puzzle can be easily solved if we know following interesting result in probability and expectation. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. Hopefully you know that the expected number of trials until success (i.e. The expectation of a geometric distribution) is 1 p 1 p. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. If probability of success is p in.
from www.chegg.com
This puzzle can be easily solved if we know following interesting result in probability and expectation. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. The expectation of a geometric distribution) is 1 p 1 p. Hopefully you know that the expected number of trials until success (i.e. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. If probability of success is p in.
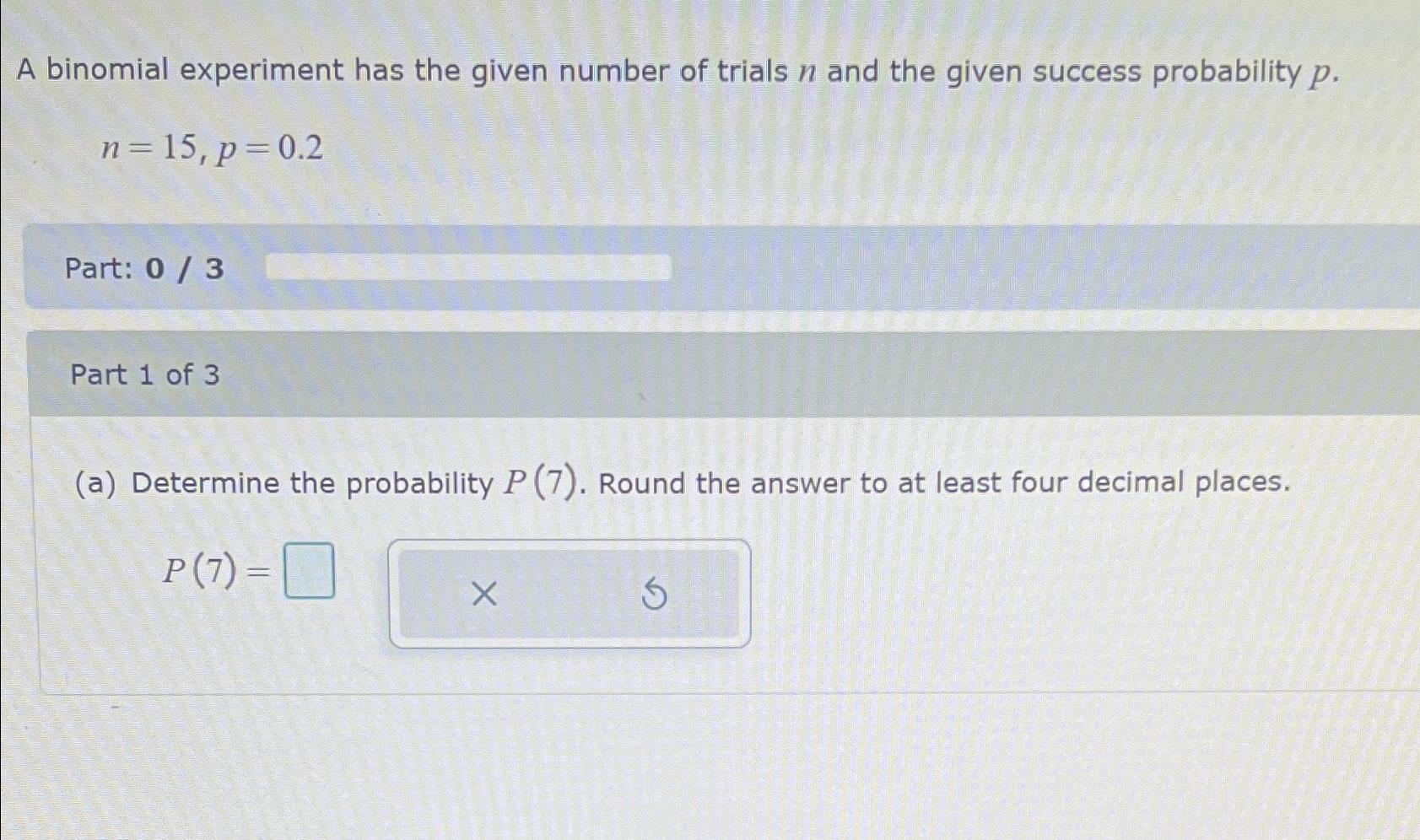
Solved A binomial experiment has the given number of trials
Expected Number Of Trials Until Success In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. The expectation of a geometric distribution) is 1 p 1 p. This puzzle can be easily solved if we know following interesting result in probability and expectation. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. If probability of success is p in. Hopefully you know that the expected number of trials until success (i.e.
From www.researchgate.net
Descriptive statistics for the total number of trials until errorfree Expected Number Of Trials Until Success Hopefully you know that the expected number of trials until success (i.e. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. If. Expected Number Of Trials Until Success.
From www.slideserve.com
PPT Probability Models PowerPoint Presentation, free download ID Expected Number Of Trials Until Success Hopefully you know that the expected number of trials until success (i.e. If probability of success is p in. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. The expectation of a geometric distribution) is 1 p 1 p. This puzzle can be easily solved if we. Expected Number Of Trials Until Success.
From www.numerade.com
SOLVED 22. In the expression ,which value represents the number of Expected Number Of Trials Until Success In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. If probability of success is p in. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. This puzzle can be easily solved if we know following interesting result. Expected Number Of Trials Until Success.
From www.researchgate.net
A. Expected completion dates of trials in 2020; B. Expected completion Expected Number Of Trials Until Success The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. The expectation of a geometric distribution) is 1 p 1 p. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. If. Expected Number Of Trials Until Success.
From censparm.blob.core.windows.net
Expected Number Of Trials Until N Successes at Gerald Mahon blog Expected Number Of Trials Until Success In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. The expectation of a geometric distribution) is 1 p 1 p. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. If probability of success is p. Expected Number Of Trials Until Success.
From www.slideteam.net
Clinical Trial Phases Graph Indicating Clinical Trial Phases Expected Number Of Trials Until Success The expectation of a geometric distribution) is 1 p 1 p. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. This. Expected Number Of Trials Until Success.
From www.chegg.com
Solved Consider a sequence of independent Bernoulli trials Expected Number Of Trials Until Success The expectation of a geometric distribution) is 1 p 1 p. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. Hopefully you know that the expected number of. Expected Number Of Trials Until Success.
From www.youtube.com
Finding the number of trials in a binomial distribution for a given Expected Number Of Trials Until Success In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. If probability of success is p in. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. Hopefully you know that the expected number of trials until success (i.e.. Expected Number Of Trials Until Success.
From censparm.blob.core.windows.net
Expected Number Of Trials Until N Successes at Gerald Mahon blog Expected Number Of Trials Until Success However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. Hopefully you know that the expected number of trials until success (i.e. If probability of success is p in. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x). Expected Number Of Trials Until Success.
From www.researchgate.net
Density plots for the number of trials until testing by preference Expected Number Of Trials Until Success The expectation of a geometric distribution) is 1 p 1 p. If probability of success is p in. Hopefully you know that the expected number of trials until success (i.e. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Geometric distribution can. Expected Number Of Trials Until Success.
From www.researchgate.net
Mean (± SE) detourreaching performance (number of trials until Expected Number Of Trials Until Success The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Hopefully you know that the expected number of trials until success (i.e. This puzzle can be easily solved if we know following interesting result in probability and expectation. However, the answer is slightly. Expected Number Of Trials Until Success.
From www.researchgate.net
Mean number of trials until participants were able to correctly Expected Number Of Trials Until Success This puzzle can be easily solved if we know following interesting result in probability and expectation. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. The expectation of a geometric distribution) is 1 p 1 p. In repeated independent trials with the same probability of success, as the number. Expected Number Of Trials Until Success.
From www.numerade.com
SOLVED What is the formula for the expected number of successes in a Expected Number Of Trials Until Success Hopefully you know that the expected number of trials until success (i.e. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. This. Expected Number Of Trials Until Success.
From censparm.blob.core.windows.net
Expected Number Of Trials Until N Successes at Gerald Mahon blog Expected Number Of Trials Until Success If probability of success is p in. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. This puzzle can be easily. Expected Number Of Trials Until Success.
From www.numerade.com
SOLVED Assume the random variable X has a binomial distribution with Expected Number Of Trials Until Success Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. The expectation of a geometric distribution) is 1 p 1 p. Hopefully you know that the expected number of trials until success (i.e. This puzzle can be easily solved if we know following interesting result in probability and expectation. The. Expected Number Of Trials Until Success.
From www.youtube.com
What is the expected number of trials until x successes? (3 Solutions Expected Number Of Trials Until Success This puzzle can be easily solved if we know following interesting result in probability and expectation. If probability of success is p in. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Geometric distribution can be defined as a discrete probability distribution. Expected Number Of Trials Until Success.
From www.slideteam.net
Graph Indicating Clinical Trial Phases Probability Of Success Clinical Expected Number Of Trials Until Success The expectation of a geometric distribution) is 1 p 1 p. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. Hopefully you know that the expected number of. Expected Number Of Trials Until Success.
From www.chegg.com
Solved 6. (Sampling until a fixed number of successes.) Expected Number Of Trials Until Success Hopefully you know that the expected number of trials until success (i.e. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. However, the answer is slightly different if. Expected Number Of Trials Until Success.
From www.slideserve.com
PPT AP Statistics Review PowerPoint Presentation, free download ID Expected Number Of Trials Until Success Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. If probability of success is p in. The expectation of a geometric distribution) is 1 p 1 p.. Expected Number Of Trials Until Success.
From kunduz.com
[ANSWERED] Find the probability of exactly two successes in six trials Expected Number Of Trials Until Success If probability of success is p in. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Geometric distribution can be. Expected Number Of Trials Until Success.
From www.researchgate.net
Predicted probability of success across age (left) and trial number Expected Number Of Trials Until Success The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. The expectation of a geometric distribution) is 1 p 1 p. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the.. Expected Number Of Trials Until Success.
From www.researchgate.net
Number of trials to learn each rule (reach the criterion of success for Expected Number Of Trials Until Success The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. This puzzle can be easily solved if we know following interesting result in probability and expectation. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want. Expected Number Of Trials Until Success.
From censparm.blob.core.windows.net
Expected Number Of Trials Until N Successes at Gerald Mahon blog Expected Number Of Trials Until Success In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. Hopefully you know that the expected number of trials until success (i.e. If probability of success is p in. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what. Expected Number Of Trials Until Success.
From www.numerade.com
SOLVED Consider a sequence of independent Bernoulli trials with p=0.2 Expected Number Of Trials Until Success The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. This puzzle can be easily solved if we know following interesting result in. Expected Number Of Trials Until Success.
From www.researchgate.net
NUMBER OF TRIALS AVERAGED FOR EACH PARTICIPANT Download Scientific Expected Number Of Trials Until Success However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Hopefully you know that the expected number of trials until success. Expected Number Of Trials Until Success.
From slideplayer.com
Chapter 16 Probability Models ppt download Expected Number Of Trials Until Success If probability of success is p in. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. This puzzle can be easily solved if we know following interesting result in probability and expectation. The expectation of a geometric distribution) is 1 p 1 p. However, the answer is slightly. Expected Number Of Trials Until Success.
From www.coursehero.com
[Solved] Shown below are the number of trials and success probability Expected Number Of Trials Until Success If probability of success is p in. This puzzle can be easily solved if we know following interesting result in probability and expectation. Hopefully you know that the expected number of trials until success (i.e. The expectation of a geometric distribution) is 1 p 1 p. However, the answer is slightly different if you are considering, say, conducting n trials. Expected Number Of Trials Until Success.
From www.numerade.com
SOLVED Basic Probability Let us consider a sequence of Bernoulli Expected Number Of Trials Until Success The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. In repeated independent trials with the same probability of success, as the number. Expected Number Of Trials Until Success.
From www.numerade.com
SOLVED Independent trials, each resulting in a success with Expected Number Of Trials Until Success If probability of success is p in. Hopefully you know that the expected number of trials until success (i.e. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. This puzzle can be easily solved if we know following interesting result in probability and expectation. In repeated independent trials with. Expected Number Of Trials Until Success.
From stats.stackexchange.com
random variable Expected number of trials when after each failed Expected Number Of Trials Until Success If probability of success is p in. The expectation of a geometric distribution) is 1 p 1 p. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1}. Expected Number Of Trials Until Success.
From www.numerade.com
SOLVED The probability histogram of _ Binomial distribution is shown Expected Number Of Trials Until Success If probability of success is p in. Hopefully you know that the expected number of trials until success (i.e. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after.. Expected Number Of Trials Until Success.
From www.chegg.com
Solved A binomial experiment has the given number of trials Expected Number Of Trials Until Success Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes is. If probability of success is p in. The expected number of trials until the first success in a geometric. Expected Number Of Trials Until Success.
From www.chegg.com
Solved 3. Consider a sequence of independent Bernoulli Expected Number Of Trials Until Success The expected number of trials until the first success in a geometric distribution is calculated as $$ e (x) = \frac {1} {p} $$, showing how it. Hopefully you know that the expected number of trials until success (i.e. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. The. Expected Number Of Trials Until Success.
From seekingalpha.com
Investor's Guide To Clinical Trials Phase Success Rates For Expected Number Of Trials Until Success However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. Geometric distribution can be defined as a discrete probability distribution that represents the probability of getting the first success after. If probability of success is p in. In repeated independent trials with the same probability of success, as. Expected Number Of Trials Until Success.
From www.slideteam.net
Graph Indicating Clinical Trial Phases Probability Of Success New Drug Expected Number Of Trials Until Success If probability of success is p in. However, the answer is slightly different if you are considering, say, conducting n trials simultaneously, and want to know what is the. The expectation of a geometric distribution) is 1 p 1 p. In repeated independent trials with the same probability of success, as the number of trials increases, the fraction of successes. Expected Number Of Trials Until Success.