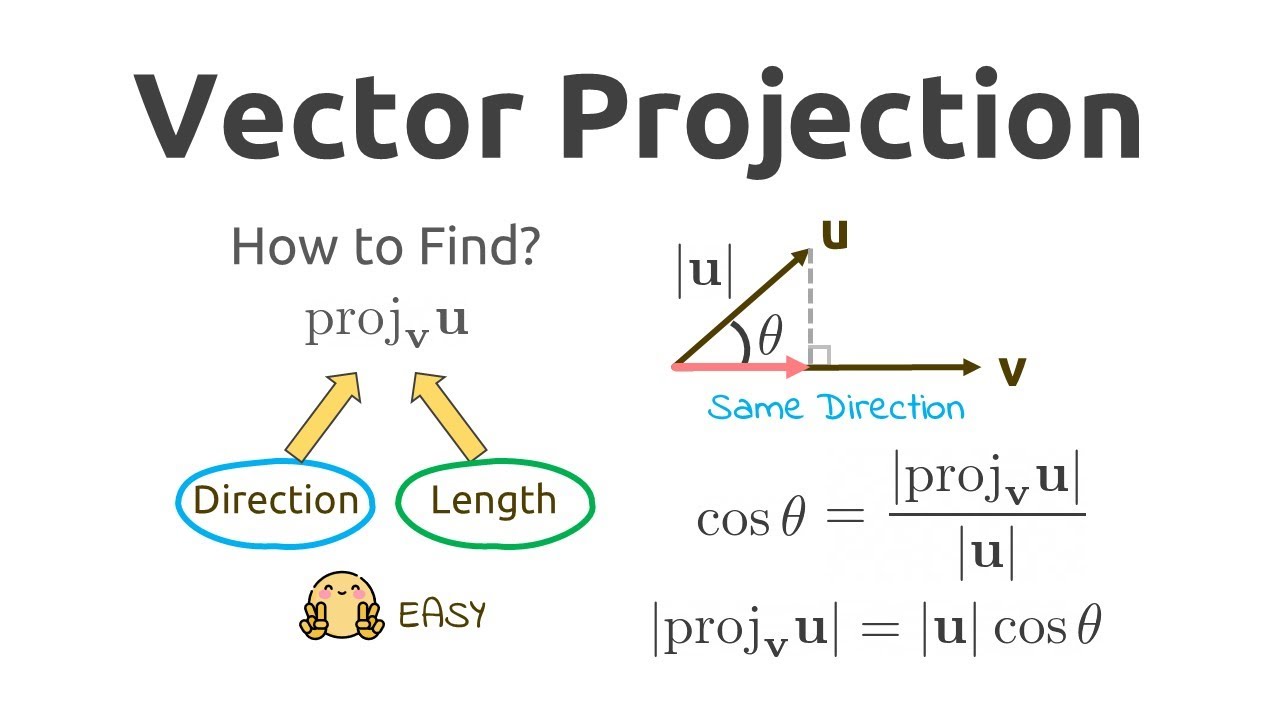
What Is The Purpose Of A Vector Projection . Let us take an example of work done. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. Vector projection is the shadow of a vector over another vector. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. Vector projections are used for determining the component of a vector along a direction. It allows you to determine how one vector influences another in a specific direction. It is obtained by multiplying the magnitude of the given vectors. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is.
from www.youtube.com
It allows you to determine how one vector influences another in a specific direction. It is obtained by multiplying the magnitude of the given vectors. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. Vector projections are used for determining the component of a vector along a direction. Vector projection is the shadow of a vector over another vector. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. Let us take an example of work done. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector.
Vector Projection and Dot Products YouTube
What Is The Purpose Of A Vector Projection Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Let us take an example of work done. It allows you to determine how one vector influences another in a specific direction. Vector projections are used for determining the component of a vector along a direction. It is obtained by multiplying the magnitude of the given vectors. Vector projection is the shadow of a vector over another vector. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is.
From www.youtube.com
Math21a. Vector Projection Equations YouTube What Is The Purpose Of A Vector Projection Let us take an example of work done. It allows you to determine how one vector influences another in a specific direction. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. Vector projection is. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vector Projection YouTube What Is The Purpose Of A Vector Projection Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. It is obtained by multiplying the magnitude of the given vectors. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is. What Is The Purpose Of A Vector Projection.
From www.geeksforgeeks.org
Vector Projection Formula, Definition, Derivation, and Examples What Is The Purpose Of A Vector Projection It is obtained by multiplying the magnitude of the given vectors. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. It allows you to determine how one vector influences another in a specific direction. Learn how to calculate the projection. What Is The Purpose Of A Vector Projection.
From www.slideserve.com
PPT Unit Vectors PowerPoint Presentation, free download ID3011813 What Is The Purpose Of A Vector Projection It allows you to determine how one vector influences another in a specific direction. Let us take an example of work done. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. The vector projection of one vector over another vector. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vector Projection and Dot Products YouTube What Is The Purpose Of A Vector Projection Let us take an example of work done. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Vector projection is the shadow of a vector over another vector. It is obtained by multiplying the magnitude of the given vectors. Learn how to calculate the projection of a. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vector Projection of u in Direction of v and Orthogonal Component YouTube What Is The Purpose Of A Vector Projection It allows you to determine how one vector influences another in a specific direction. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. Let us take an example of work done. It is obtained by multiplying the magnitude of the given vectors. Vector projection is the shadow of. What Is The Purpose Of A Vector Projection.
From www.slideserve.com
PPT Machine Learning Math Essentials Part 2 PowerPoint Presentation What Is The Purpose Of A Vector Projection It is obtained by multiplying the magnitude of the given vectors. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Let us take an example of work done. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude. What Is The Purpose Of A Vector Projection.
From us.europedias.com
Vector Projection Formula Explained Ideas of Europedias What Is The Purpose Of A Vector Projection Let us take an example of work done. It allows you to determine how one vector influences another in a specific direction. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. Learn how to calculate the projection of a vector. What Is The Purpose Of A Vector Projection.
From www.researchgate.net
Schematic illustration of the projection of a vector... Download What Is The Purpose Of A Vector Projection Vector projections are used for determining the component of a vector along a direction. Vector projection is the shadow of a vector over another vector. Let us take an example of work done. It is obtained by multiplying the magnitude of the given vectors. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. Learn how to. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vector Projections Data Science Basics YouTube What Is The Purpose Of A Vector Projection Let us take an example of work done. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. The vector projection is the vector produced when one vector is resolved into two component vectors, one. What Is The Purpose Of A Vector Projection.
From www.slideserve.com
PPT Vector Refresher Part 3 PowerPoint Presentation, free download What Is The Purpose Of A Vector Projection Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. It is obtained by multiplying the magnitude of the given vectors. It allows you to determine how one vector influences another in a specific direction. Vector projection is the shadow of a vector over another vector. Let us take an example of work done. Vector projections are. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Geometric Representation of Projection of Vectors YouTube What Is The Purpose Of A Vector Projection It allows you to determine how one vector influences another in a specific direction. Vector projection is the shadow of a vector over another vector. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Learn how to calculate the projection of a vector onto another vector using. What Is The Purpose Of A Vector Projection.
From medium.com
LINEAR ALGEBRA FOR DATA SCIENCE AND MACHINE LEARNING by Swastik Nayak What Is The Purpose Of A Vector Projection Vector projections are used for determining the component of a vector along a direction. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. Vector projection is the shadow of a vector over another vector. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the. What Is The Purpose Of A Vector Projection.
From www2.seas.gwu.edu
Linear Algebra What Is The Purpose Of A Vector Projection Vector projections are used for determining the component of a vector along a direction. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. Let us take an example of work done. It allows you to determine how one vector influences another in a specific direction. Vector projection is the shadow of a vector over another vector.. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vector Projection on Coordinate Plane Q2 YouTube What Is The Purpose Of A Vector Projection Vector projection is the shadow of a vector over another vector. Vector projections are used for determining the component of a vector along a direction. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. The vector projection is the vector produced when one vector is resolved into. What Is The Purpose Of A Vector Projection.
From www.teachoo.com
Find the projection of the vector a = 2i + 3j + 2k on vector b=i+2j+k What Is The Purpose Of A Vector Projection It allows you to determine how one vector influences another in a specific direction. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. The vector projection. What Is The Purpose Of A Vector Projection.
From www.cuemath.com
Vector Projection Formula Learn to Find the Vector Projection What Is The Purpose Of A Vector Projection Let us take an example of work done. It is obtained by multiplying the magnitude of the given vectors. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. The vector projection of one vector over another vector is the length of the shadow of the given vector over. What Is The Purpose Of A Vector Projection.
From vectorified.com
Vector Projection at Collection of Vector Projection What Is The Purpose Of A Vector Projection Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. It is obtained by multiplying the magnitude of the given vectors. The vector projection is the vector produced when one vector is resolved into two. What Is The Purpose Of A Vector Projection.
From www.teachoo.com
Example 16 Find projection of vector a = 2i + 3j + 2k on b What Is The Purpose Of A Vector Projection Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. It allows you to determine how one vector influences another in a specific direction. Projection in \(\mathbb{r}^3\). What Is The Purpose Of A Vector Projection.
From www.youtube.com
Calculus 3 Vector Projections & Orthogonal Components YouTube What Is The Purpose Of A Vector Projection Let us take an example of work done. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Vector projection is the shadow of a vector over another vector. It allows you to determine how one vector influences another in a specific direction. The vector projection is the. What Is The Purpose Of A Vector Projection.
From www.slideserve.com
PPT PROJECTION PowerPoint Presentation, free download ID433878 What Is The Purpose Of A Vector Projection Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. The vector projection is the vector produced when one vector is resolved into two component vectors, one. What Is The Purpose Of A Vector Projection.
From www.slideserve.com
PPT Vectors MM1 module 4 PowerPoint Presentation, free download ID What Is The Purpose Of A Vector Projection The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Let us take an example of work done. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. It is obtained by multiplying the magnitude of the given vectors. The vector projection is the vector. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Understanding Vector Projections YouTube What Is The Purpose Of A Vector Projection Let us take an example of work done. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Vector projection is the shadow of a vector over another vector. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. It allows you to determine how. What Is The Purpose Of A Vector Projection.
From bitdrivencircuits.com
Vector Math/Formulas (2D and 3D) What Is The Purpose Of A Vector Projection Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. Let us take an example of work done. It is obtained by multiplying the magnitude of the given vectors. The vector projection of one vector over another vector is the length of the shadow of the given vector over. What Is The Purpose Of A Vector Projection.
From ilc.upd.edu.ph
Vectors and their Projections Interactive Learning Center Diliman What Is The Purpose Of A Vector Projection It is obtained by multiplying the magnitude of the given vectors. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. It allows you to determine how one vector influences another in a specific direction. Vector projections are used for determining the component of a vector along a direction. Learn how to calculate the projection of a. What Is The Purpose Of A Vector Projection.
From www.teachertube.com
Proving the Vector Projection Formula What Is The Purpose Of A Vector Projection The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. It is obtained by multiplying the magnitude of the given vectors. It allows you to determine how one vector influences another in a specific direction. The vector projection of one vector. What Is The Purpose Of A Vector Projection.
From calconcalculator.com
Vector Projection Calculator Solution with Steps 2D, 3D What Is The Purpose Of A Vector Projection It is obtained by multiplying the magnitude of the given vectors. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. Let us take an example of work done. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vector Projection VS Vector Component YouTube What Is The Purpose Of A Vector Projection The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. It allows you to determine how one vector influences. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Orthogonal projection of a vector onto a plane. YouTube What Is The Purpose Of A Vector Projection Vector projections are used for determining the component of a vector along a direction. Vector projection is the shadow of a vector over another vector. Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. It allows you to determine how one vector influences another in a specific direction.. What Is The Purpose Of A Vector Projection.
From www.youtube.com
The Dot Product Vector and Scalar Projections YouTube What Is The Purpose Of A Vector Projection Vector projections are used for determining the component of a vector along a direction. It allows you to determine how one vector influences another in a specific direction. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. Learn how to calculate the projection of a vector onto. What Is The Purpose Of A Vector Projection.
From www.youtube.com
How to find Projection of one Vector on other Vector class 12 What Is The Purpose Of A Vector Projection Learn how to calculate the projection of a vector onto another vector using the dot product and the magnitude of the. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in. What Is The Purpose Of A Vector Projection.
From mathsathome.com
How to Calculate Scalar and Vector Projections What Is The Purpose Of A Vector Projection Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. The vector projection of one vector over another vector is the length of the shadow of the given vector over another vector. It is obtained by multiplying the magnitude of the given vectors. Learn how to calculate the projection of a vector onto another vector using the. What Is The Purpose Of A Vector Projection.
From zief0002.github.io
Chapter 5 Vector Geometry Angles, Projection, and What Is The Purpose Of A Vector Projection The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. Learn how to calculate the projection of a vector onto another vector using the dot product and the. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vectors Projection Vector YouTube What Is The Purpose Of A Vector Projection Let us take an example of work done. Vector projection is the shadow of a vector over another vector. Projection in \(\mathbb{r}^3\) 011946 the vector \(\mathbf{u}_{1} = \longvect{qp}_{1}\) in figure [fig:011945] is. It allows you to determine how one vector influences another in a specific direction. Vector projections are used for determining the component of a vector along a direction.. What Is The Purpose Of A Vector Projection.
From www.youtube.com
Vector Projection, Multivariable Calculus YouTube What Is The Purpose Of A Vector Projection Vector projections are used for determining the component of a vector along a direction. The vector projection is the vector produced when one vector is resolved into two component vectors, one that is parallel to the second vector and one that is perpendicular. The vector projection of one vector over another vector is the length of the shadow of the. What Is The Purpose Of A Vector Projection.