Axes Of A Triangle . The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. It is the radical line of the coaxal system consisting of. In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: What is the length, in units, of vector hi? If you were asked if this graph is symmetric about either axis, you would say, yes;. Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. The integration techniques demonstrated can be used to find the moment of inertia of any two. Find the moment of inertia (2nd moment of area) of a triangle about any axis:
from geocities.ws
If you were asked if this graph is symmetric about either axis, you would say, yes;. Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. It is the radical line of the coaxal system consisting of. In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. What is the length, in units, of vector hi? Find the moment of inertia (2nd moment of area) of a triangle about any axis: The integration techniques demonstrated can be used to find the moment of inertia of any two.
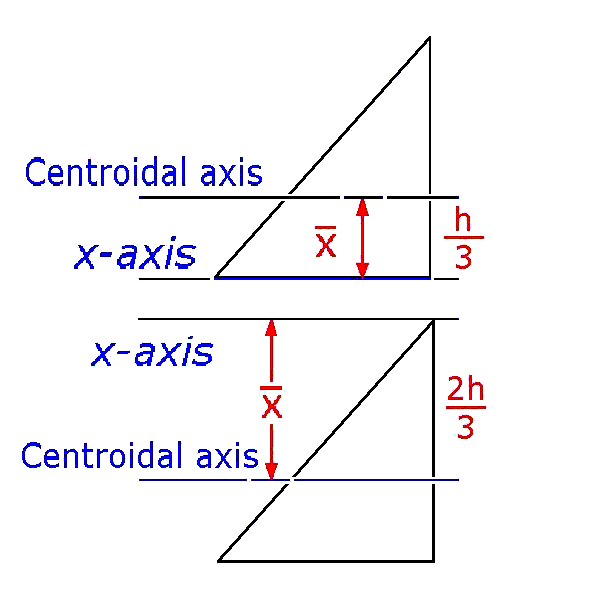
Moment of Area Formulas Circles, Triangles, and Rectangles
Axes Of A Triangle The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: Find the moment of inertia (2nd moment of area) of a triangle about any axis: What is the length, in units, of vector hi? The integration techniques demonstrated can be used to find the moment of inertia of any two. If you were asked if this graph is symmetric about either axis, you would say, yes;. Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. It is the radical line of the coaxal system consisting of.
From byjus.com
If 3x 4y + 12 = 0 and 3x + 2y 6 = 0, then area of triangle formed Axes Of A Triangle It is the radical line of the coaxal system consisting of. If you were asked if this graph is symmetric about either axis, you would say, yes;. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. The integration techniques demonstrated can be used to find. Axes Of A Triangle.
From www.nagwa.com
Question Video Finding the Equation of a Plane Cutting the Coordinate Axes Of A Triangle If you were asked if this graph is symmetric about either axis, you would say, yes;. It is the radical line of the coaxal system consisting of. In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: What is the length, in units, of vector hi?. Axes Of A Triangle.
From undergroundmathematics.org
Solution A line cuts the axes to make a triangle; can we find its Axes Of A Triangle The integration techniques demonstrated can be used to find the moment of inertia of any two. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. If you were asked if this graph is symmetric about either axis, you would say, yes;. It is the radical. Axes Of A Triangle.
From solvedlib.com
Triangles ABC and RST are graphed on the set e of axe… SolvedLib Axes Of A Triangle The integration techniques demonstrated can be used to find the moment of inertia of any two. What is the length, in units, of vector hi? If you were asked if this graph is symmetric about either axis, you would say, yes;. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the. Axes Of A Triangle.
From byjus.com
A triangle has two of its sides along the axes , its third side touches Axes Of A Triangle If you were asked if this graph is symmetric about either axis, you would say, yes;. Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. What is the. Axes Of A Triangle.
From www.youtube.com
The incentre of the triangle formed by axes and the line x/a+y/b=1is Axes Of A Triangle If you were asked if this graph is symmetric about either axis, you would say, yes;. It is the radical line of the coaxal system consisting of. Find the moment of inertia (2nd moment of area) of a triangle about any axis: The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition). Axes Of A Triangle.
From vtuupdates.com
Derive an expression for moment of inertia of a triangle from first Axes Of A Triangle What is the length, in units, of vector hi? In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in. Axes Of A Triangle.
From www.geogebra.org
Rotating a Triangle Around a Coordinate Axis GeoGebra Axes Of A Triangle It is the radical line of the coaxal system consisting of. Find the moment of inertia (2nd moment of area) of a triangle about any axis: In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: The orthic axis is the perspectrix of the medial triangle. Axes Of A Triangle.
From www.geogebra.org
Reflecting a triangle across the xaxis and the yaxis GeoGebra Axes Of A Triangle In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: The integration techniques demonstrated can be used to find the moment of inertia of any two. What is the length, in units, of vector hi? The orthic axis is the perspectrix of the medial triangle and. Axes Of A Triangle.
From www.britannica.com
Trigonometry Polar Coordinates Britannica Axes Of A Triangle In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: The integration techniques demonstrated can be used to find the moment of inertia of any two. If you were asked if this graph is symmetric about either axis, you would say, yes;. The orthic axis is. Axes Of A Triangle.
From mungfali.com
Triangle Reflection Across Y Axis Axes Of A Triangle Find the moment of inertia (2nd moment of area) of a triangle about any axis: If you were asked if this graph is symmetric about either axis, you would say, yes;. The integration techniques demonstrated can be used to find the moment of inertia of any two. It is the radical line of the coaxal system consisting of. The orthic. Axes Of A Triangle.
From gogeometry.com
Math, Geometry Problem 1233 Triangle, Euler Line, Orthic Axis Axes Of A Triangle The integration techniques demonstrated can be used to find the moment of inertia of any two. Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. Find the moment. Axes Of A Triangle.
From fatima-jolpblogmccormick.blogspot.com
Different Axis in Figures How to Explain Axes Of A Triangle Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the. Axes Of A Triangle.
From www.teachoo.com
Line of Symmetry of Isoceles Triangle [Explained] Teachoo Axes Of A Triangle It is the radical line of the coaxal system consisting of. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\). Axes Of A Triangle.
From www.youtube.com
Coordinate Geometry Area of triangle formed by x,y axes and line Axes Of A Triangle It is the radical line of the coaxal system consisting of. Find the moment of inertia (2nd moment of area) of a triangle about any axis: Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive. Axes Of A Triangle.
From www.teachoo.com
Ex 10.1, 2 Base of an equilateral triangle with side 2a Axes Of A Triangle The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. If you were asked if this graph is symmetric about either axis, you would say, yes;. It is the radical line of the coaxal system consisting of. The integration techniques demonstrated can be used to find. Axes Of A Triangle.
From www.mashupmath.com
Reflection Over The X and Y Axis The Complete Guide — Mashup Math Axes Of A Triangle Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the. Axes Of A Triangle.
From www.cuemath.com
How many lines of symmetry does an equilateral triangle have? [Solved] Axes Of A Triangle If you were asked if this graph is symmetric about either axis, you would say, yes;. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. What is the length, in units, of vector hi? The integration techniques demonstrated can be used to find the moment. Axes Of A Triangle.
From www.mometrix.com
Axis of Symmetry Overview (Sample Questions) Axes Of A Triangle What is the length, in units, of vector hi? If you were asked if this graph is symmetric about either axis, you would say, yes;. The integration techniques demonstrated can be used to find the moment of inertia of any two. In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of. Axes Of A Triangle.
From vtuupdates.com
Derive an expression for moment of inertia of a triangle from first Axes Of A Triangle Find the moment of inertia (2nd moment of area) of a triangle about any axis: What is the length, in units, of vector hi? It is the radical line of the coaxal system consisting of. The integration techniques demonstrated can be used to find the moment of inertia of any two. Given points \ (a (x_1, y_1)\) and \ (b. Axes Of A Triangle.
From www.youtube.com
Moment of Inertia of a Triangle About Its Centroidal Axes YouTube Axes Of A Triangle The integration techniques demonstrated can be used to find the moment of inertia of any two. Find the moment of inertia (2nd moment of area) of a triangle about any axis: Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio. Axes Of A Triangle.
From www.topperlearning.com
Draw the graphs of the pair of linear equations xy=2=0 & 4xy4=0 Axes Of A Triangle If you were asked if this graph is symmetric about either axis, you would say, yes;. What is the length, in units, of vector hi? The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. It is the radical line of the coaxal system consisting of.. Axes Of A Triangle.
From www.numerade.com
GEOMETRY A right triangle is formed in the first quadrant by the x and Axes Of A Triangle Find the moment of inertia (2nd moment of area) of a triangle about any axis: The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of. Axes Of A Triangle.
From www.chegg.com
Solved For the triangle shown to the right, determine (a) Axes Of A Triangle Find the moment of inertia (2nd moment of area) of a triangle about any axis: In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: It is the radical line of the coaxal system consisting of. Given points \ (a (x_1, y_1)\) and \ (b (x_2,. Axes Of A Triangle.
From www.teachoo.com
Line of Symmetry of Isoceles Triangle [Explained] Teachoo Axes Of A Triangle What is the length, in units, of vector hi? In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: If you were asked if this graph is symmetric about either axis, you would say, yes;. Find the moment of inertia (2nd moment of area) of a. Axes Of A Triangle.
From geocities.ws
Moment of Area Formulas Circles, Triangles, and Rectangles Axes Of A Triangle What is the length, in units, of vector hi? If you were asked if this graph is symmetric about either axis, you would say, yes;. Find the moment of inertia (2nd moment of area) of a triangle about any axis: Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides. Axes Of A Triangle.
From www.calcresource.com
Moment of Inertia of a Triangle calcresource Axes Of A Triangle What is the length, in units, of vector hi? The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. Find the moment of inertia (2nd moment of area) of a triangle about any axis: The integration techniques demonstrated can be used to find the moment of. Axes Of A Triangle.
From www.toppr.com
Find the moment of inertia of a plate cut in shape of a right angled Axes Of A Triangle What is the length, in units, of vector hi? It is the radical line of the coaxal system consisting of. If you were asked if this graph is symmetric about either axis, you would say, yes;. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle.. Axes Of A Triangle.
From math.stackexchange.com
calculus The sides of a right triangle are on the coordinate axes and Axes Of A Triangle The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. What is the length, in units, of vector hi? Find the moment of inertia (2nd moment of area) of a triangle about any axis: In following sections we will use the integral definitions of moment of. Axes Of A Triangle.
From www.geogebra.org
Axes de symétrie d'un triangle isocèleequilatéral GeoGebra Axes Of A Triangle In following sections we will use the integral definitions of moment of inertia (10.1.3) to find the moments of inertia of five common shapes: Find the moment of inertia (2nd moment of area) of a triangle about any axis: If you were asked if this graph is symmetric about either axis, you would say, yes;. Given points \ (a (x_1,. Axes Of A Triangle.
From www.toppr.com
The area of the triangle formed by the tangent drawn at the point Axes Of A Triangle Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. What is the length, in units, of vector hi? The integration techniques demonstrated can be used to find the. Axes Of A Triangle.
From www.kristakingmath.com
Reflecting figures in coordinate space — Krista King Math Online math Axes Of A Triangle What is the length, in units, of vector hi? Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that divides the line segment \ (ab\) internally in the ratio \ (m:n\), we can derive the coordinates of point \ (p\) using. The integration techniques demonstrated can be used to find the. Axes Of A Triangle.
From mungfali.com
The Formula Of A Triangle Axes Of A Triangle It is the radical line of the coaxal system consisting of. If you were asked if this graph is symmetric about either axis, you would say, yes;. The integration techniques demonstrated can be used to find the moment of inertia of any two. Find the moment of inertia (2nd moment of area) of a triangle about any axis: What is. Axes Of A Triangle.
From engineerexcel.com
Parallel Axis Theorem for Area Moment of Inertia EngineerExcel Axes Of A Triangle If you were asked if this graph is symmetric about either axis, you would say, yes;. The orthic axis is the perspectrix of the medial triangle and tangential triangle, as well as (by definition) the orthic triangle and reference triangle. What is the length, in units, of vector hi? The integration techniques demonstrated can be used to find the moment. Axes Of A Triangle.
From www.geogebra.org
Rotating a triangle around the y axis GeoGebra Axes Of A Triangle What is the length, in units, of vector hi? If you were asked if this graph is symmetric about either axis, you would say, yes;. The integration techniques demonstrated can be used to find the moment of inertia of any two. Given points \ (a (x_1, y_1)\) and \ (b (x_2, y_2)\) and a point \ (p (x, y)\) that. Axes Of A Triangle.