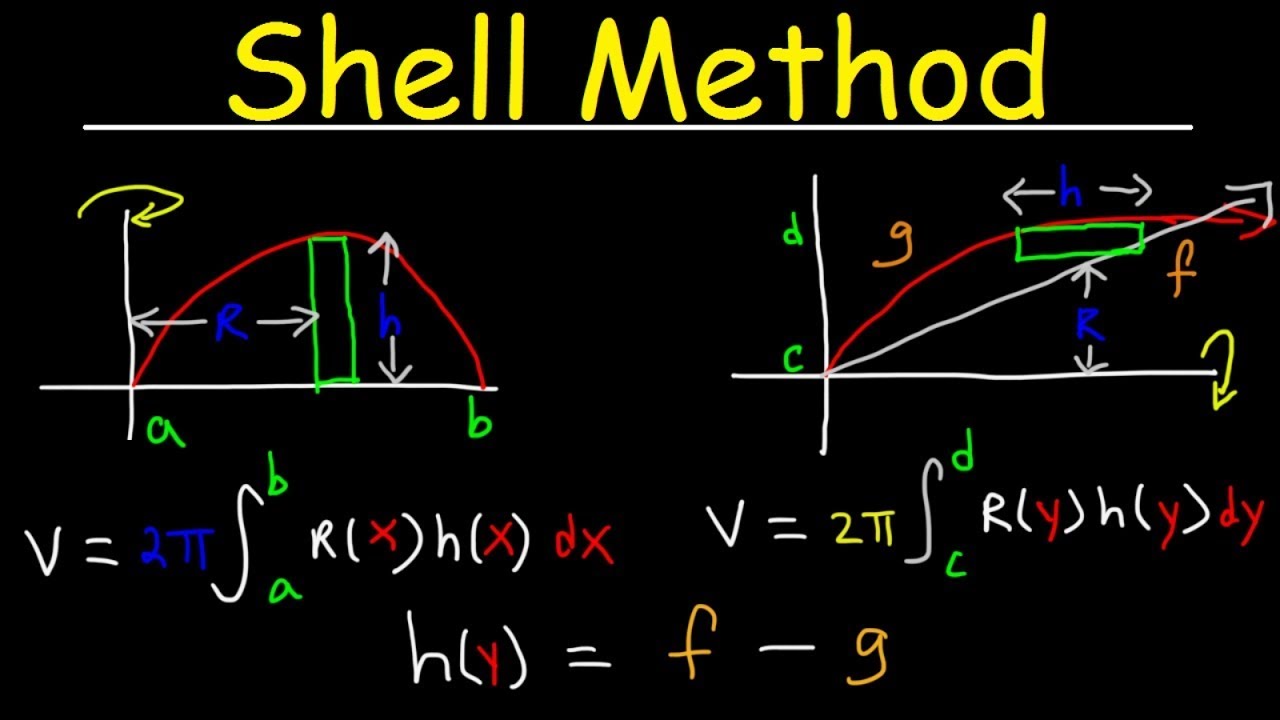
Cylindrical Shell Method With Two Functions at Douglas Jacobson blog

Cylindrical Shell Method With Two Functions. Stepping it up a notch, our solid is now defined in terms of two separate functions. However, with the disk and washer methods, we integrate along the coordinate axis parallel to the axis of revolution. A typical cylindrical shell (in green) is also shown and can be In this section, we examine the method of cylindrical shells, the final method for finding the volume of a solid of revolution. The following steps outline how to employ the shell method. Let's look at an example: You can eneter your own functions (g(x) must be less than f(x) for all x in the interval [a,b] !). We can use this method on the same kinds of solids as the disk method or the washer method; Construct an arbitrary cylindrical shell parallel to the axis of rotation.

You can eneter your own functions (g(x) must be less than f(x) for all x in the interval [a,b] !). We can use this method on the same kinds of solids as the disk method or the washer method; Construct an arbitrary cylindrical shell parallel to the axis of rotation. In this section, we examine the method of cylindrical shells, the final method for finding the volume of a solid of revolution. A typical cylindrical shell (in green) is also shown and can be However, with the disk and washer methods, we integrate along the coordinate axis parallel to the axis of revolution. Stepping it up a notch, our solid is now defined in terms of two separate functions. Let's look at an example: The following steps outline how to employ the shell method.

√ Shell Method Formula About Y Axis What S The Difference Between

Cylindrical Shell Method With Two Functions Construct an arbitrary cylindrical shell parallel to the axis of rotation. You can eneter your own functions (g(x) must be less than f(x) for all x in the interval [a,b] !). Let's look at an example: Construct an arbitrary cylindrical shell parallel to the axis of rotation. We can use this method on the same kinds of solids as the disk method or the washer method; Stepping it up a notch, our solid is now defined in terms of two separate functions. A typical cylindrical shell (in green) is also shown and can be However, with the disk and washer methods, we integrate along the coordinate axis parallel to the axis of revolution. In this section, we examine the method of cylindrical shells, the final method for finding the volume of a solid of revolution. The following steps outline how to employ the shell method.

throw with arm holes - nutcracker original choreography - cat key hook amazon - mushrooms coffee table book - premier league cup u21 final - how to make sofas out of pallets - zebra print cushions grey - long vest name - weight loss shot that starts with s - why is my electric water heater overheating - houses for sale rhosili road cefn hengoed - terrine legumes macedoine - powershell get windows patches installed - grapefruit peel face mask - are brake pads universal - tarot cards for each zodiac sign - antirock sway bar universal - what are chocolate pillow - workout girl cartoon - cake the whip smart hair mask reviews - are pioneer woman pots dishwasher safe - led rope lights marine - what goes with colby cheese - vw beetle headliner replacement cost - where are potato chips made - silver 925 jewellery price in india