What Is The Cardinality Of Set C at Kurt Chitty blog

What Is The Cardinality Of Set C. Let a = {1, 2, 3, 4, 5, 6} and b. The cardinal of a set is the number of different elements it contains. Cardinality of a set can be defined as the number of elements present in the set. If a contains exactly n elements, where n ≥ 0, then we say that the set a is finite and its cardinality is equal to the. The cardinality of a set is the total number of elements present in the set. The cardinality of a set is defined as the number of elements in a mathematical set. The cardinality of the set a is often notated as | a | or n (a) example 12. Cardinality of a finite set refers to the number of elements in the set. The cardinal of a set a is represented by |a| or card (a). If a set s is finite, its cardinality is simply the count of. It can be countable or uncountable, finite or infinite. The number of elements in a set is the cardinality of that set. It can be finite or infinite. For example, the cardinality of the set a = {1, 2, 3, 4, 5, 6} is equal to 6 because. Cardinality refers to the concept of the “size” or “count” of a set.

It can be countable or uncountable, finite or infinite. The cardinal of a set is the number of different elements it contains. The cardinal of a set a is represented by |a| or card (a). The cardinality of the set a is often notated as | a | or n (a) example 12. The cardinality of a set is the total number of elements present in the set. It can be finite or infinite. Cardinality refers to the concept of the “size” or “count” of a set. The number of elements in a set is the cardinality of that set. Let a = {1, 2, 3, 4, 5, 6} and b. Cardinality of a set can be defined as the number of elements present in the set.

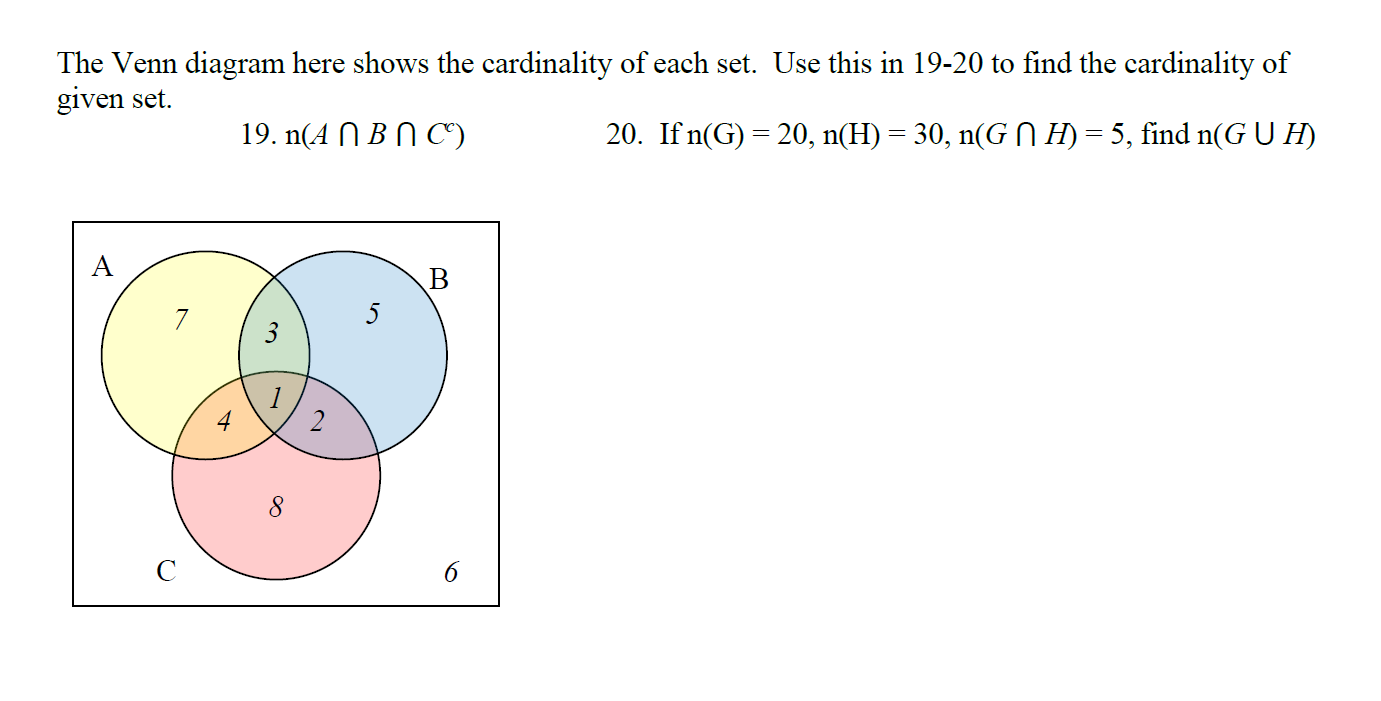
Solved The Venn diagram here shows the cardinality of each

What Is The Cardinality Of Set C It can be countable or uncountable, finite or infinite. Cardinality of a set can be defined as the number of elements present in the set. For example, the cardinality of the set a = {1, 2, 3, 4, 5, 6} is equal to 6 because. The cardinality of a set is the total number of elements present in the set. Let a = {1, 2, 3, 4, 5, 6} and b. The number of elements in a set is the cardinality of that set. If a contains exactly n elements, where n ≥ 0, then we say that the set a is finite and its cardinality is equal to the. The cardinal of a set a is represented by |a| or card (a). If a set s is finite, its cardinality is simply the count of. Cardinality refers to the concept of the “size” or “count” of a set. The cardinality of the set a is often notated as | a | or n (a) example 12. It can be countable or uncountable, finite or infinite. It can be finite or infinite. The cardinal of a set is the number of different elements it contains. Cardinality of a finite set refers to the number of elements in the set. The cardinality of a set is defined as the number of elements in a mathematical set.