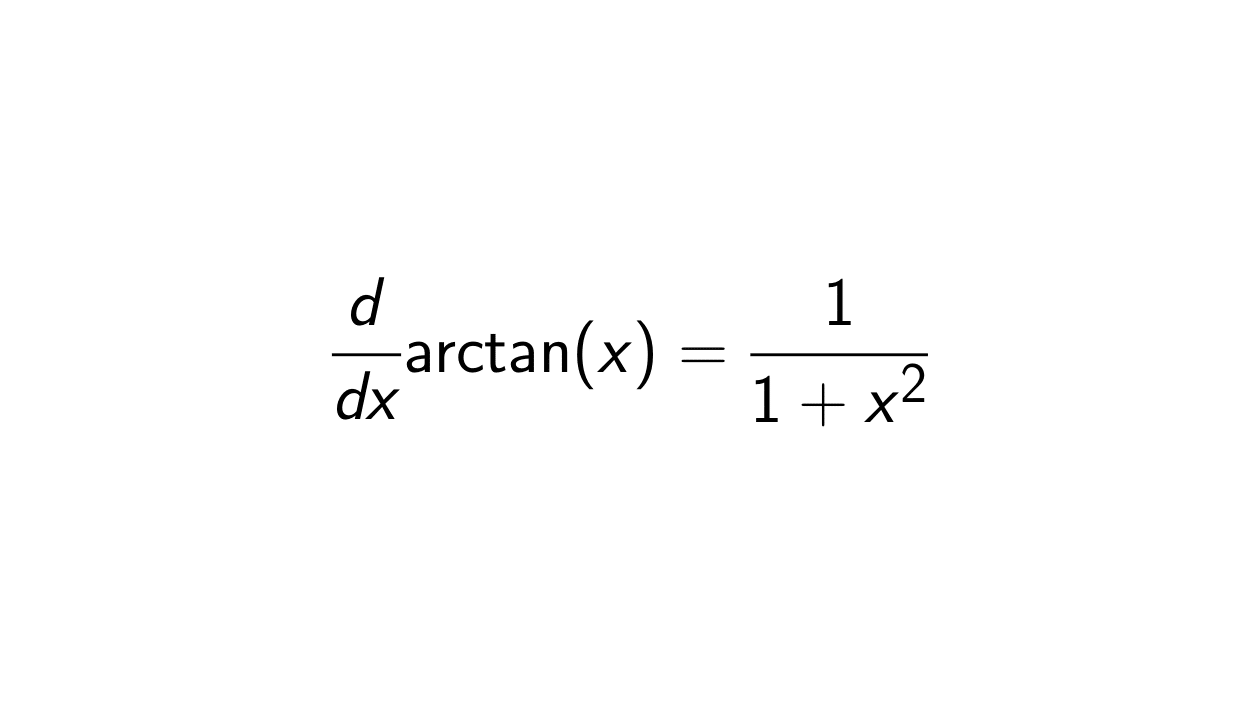Arc Tan Examples . Given arctan() = θ, we can find that tan(θ) =. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below. Tan (π / 3) = √3 ⇒. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. In the right triangle, the base is 23 m and the height is. Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. Let’s look at some examples to understand it more clearly. In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. Given below are some examples that can help us understand how the arctan function works: Also, we will learn the formulas, derivative, and integral of tan inverse x along.
from www.epsilonify.com
Given below are some examples that can help us understand how the arctan function works: Given arctan() = θ, we can find that tan(θ) =. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. Tan (π / 3) = √3 ⇒. Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Let’s look at some examples to understand it more clearly. Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. In the right triangle, the base is 23 m and the height is.
What is the Derivative of arctan(x)? Epsilonify
Arc Tan Examples Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. Also, we will learn the formulas, derivative, and integral of tan inverse x along. Given below are some examples that can help us understand how the arctan function works: Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. In the right triangle, the base is 23 m and the height is. Tan (π / 3) = √3 ⇒. Given arctan() = θ, we can find that tan(θ) =. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. Let’s look at some examples to understand it more clearly. Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below.
From www.flickr.com
arctan example related one Flickr Arc Tan Examples Given arctan() = θ, we can find that tan(θ) =. Given below are some examples that can help us understand how the arctan function works: In the right triangle, the base is 23 m and the height is. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted. Arc Tan Examples.
From www.analyzemath.com
Graph, Domain and Range of Arctan(x) function Arc Tan Examples Given arctan() = θ, we can find that tan(θ) =. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos. Arc Tan Examples.
From animalia-life.club
Arctan Graph With Points Arc Tan Examples Given below are some examples that can help us understand how the arctan function works: Given arctan() = θ, we can find that tan(θ) =. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. Tan (π / 3) = √3 ⇒. Tan (π / 2) =. Arc Tan Examples.
From educationspike.com
Derivative of Arctan Formula & Examples Education Spike Arc Tan Examples Tan (π / 3) = √3 ⇒. Let’s look at some examples to understand it more clearly. In the right triangle, the base is 23 m and the height is. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Given arctan() = θ, we can. Arc Tan Examples.
From www.cuemath.com
Inverse Tan (Inverse Tangent) Formula, Graph Tan Inverse x Arc Tan Examples Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Tan (π / 3) = √3 ⇒. Also, we will learn the formulas, derivative, and integral of tan inverse x along. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos. Arc Tan Examples.
From www.varsitytutors.com
Arcsin, Arccos, Arctan Trigonometry Arc Tan Examples Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below. Given arctan() = θ, we can find that tan(θ) =. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. Tan (π / 3) = √3 ⇒. Here, we will study. Arc Tan Examples.
From studywell.com
Inverse Trigonometric Functions Arcsin, Arccos And Arctan Arc Tan Examples Let’s look at some examples to understand it more clearly. Also, we will learn the formulas, derivative, and integral of tan inverse x along. In the right triangle, the base is 23 m and the height is. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. Since is not. Arc Tan Examples.
From www.youtube.com
How to Write in Algebraic Form csc(arctan(x/sqrt(2)) YouTube Arc Tan Examples Given arctan() = θ, we can find that tan(θ) =. In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. Also, we will learn the formulas, derivative, and integral of tan inverse x along. Since is not one of the ratios for the special angles, we can use a right. Arc Tan Examples.
From www.cuemath.com
Differentiation of Trigonometric Functions Trig Derivatives Arc Tan Examples Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. Tan (π / 3) = √3 ⇒. Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to.. Arc Tan Examples.
From www.youtube.com
Indefinite Integral of 25/(1 + 25x^2) using arctangent YouTube Arc Tan Examples Given below are some examples that can help us understand how the arctan function works: In the right triangle, the base is 23 m and the height is. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. Since is not one of the ratios for the special angles, we. Arc Tan Examples.
From www.youtube.com
Derivative of Inverse Tangent (Arctan) with example YouTube Arc Tan Examples Given arctan() = θ, we can find that tan(θ) =. Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below. In the right triangle, the base is 23 m and the height is. Tan (π / 3) = √3 ⇒. Given below are some examples that can help us understand how. Arc Tan Examples.
From www.cuemath.com
Arctan Formula, Graph, Identities, Domain and Range Arctan x Arc Tan Examples Also, we will learn the formulas, derivative, and integral of tan inverse x along. Given below are some examples that can help us understand how the arctan function works: Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. In the right triangle, the base is 23 m and the. Arc Tan Examples.
From study.com
Arctan Definition, Function & Formula Video & Lesson Transcript Arc Tan Examples Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below. Tan (π / 3) = √3 ⇒. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \. Arc Tan Examples.
From www.geeksforgeeks.org
How to find arctangent with Examples Arc Tan Examples Tan (π / 3) = √3 ⇒. Given below are some examples that can help us understand how the arctan function works: In the right triangle, the base is 23 m and the height is. In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. Let’s look at some examples. Arc Tan Examples.
From r-craft.org
How to Use the Numpy Arctan Function RCraft Arc Tan Examples The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\),. Arc Tan Examples.
From www.cuemath.com
Trigonometric Table Trigonometric Values Understanding Trig Table Arc Tan Examples The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Arctan formula is used in solving various trigonometric problems and the same is. Arc Tan Examples.
From www.profmatt.com
cribsheets — Matthew Handy Maths + Physics tutor in Harrogate Arc Tan Examples The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. Since is not one of the ratios for the special angles, we can use a right triangle. Arc Tan Examples.
From www.voovers.com
Derivative of arctan(x) (Inverse tangent) Detailed Lesson Arc Tan Examples Also, we will learn the formulas, derivative, and integral of tan inverse x along. In the right triangle, the base is 23 m and the height is. Given below are some examples that can help us understand how the arctan function works: Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain,. Arc Tan Examples.
From www.analyzemath.com
Graph, Domain and Range of Arctan(x) function Arc Tan Examples Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. Tan (π / 3) = √3 ⇒. Also, we will learn the formulas, derivative, and integral of tan inverse x along. Given arctan() = θ, we can find that tan(θ) =. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \. Arc Tan Examples.
From www.youtube.com
Differentiation of arctan 1 example YouTube Arc Tan Examples Let’s look at some examples to understand it more clearly. Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. Given below are some examples that can help us understand how the arctan function works: Also, we will learn. Arc Tan Examples.
From lunlun.com
The derivative of arctan (formula and example) Arc Tan Examples Also, we will learn the formulas, derivative, and integral of tan inverse x along. In the right triangle, the base is 23 m and the height is. Let’s look at some examples to understand it more clearly. Given below are some examples that can help us understand how the arctan function works: The arctan function takes an input value, x. Arc Tan Examples.
From lessonlibperforates.z22.web.core.windows.net
How To Get The Tangent In Math Arc Tan Examples Given below are some examples that can help us understand how the arctan function works: Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below. Tan (π / 3) = √3 ⇒. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan. Arc Tan Examples.
From www.youtube.com
Evaluating Inverse Trigonometric Functions (arcsin, arccos, arctan Arc Tan Examples Let’s look at some examples to understand it more clearly. Given below are some examples that can help us understand how the arctan function works: In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos. Arc Tan Examples.
From www.epsilonify.com
What is the Derivative of arctan(x)? Epsilonify Arc Tan Examples Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below. In the right triangle, the base is 23 m and the height is. Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. The arctan function takes an input value, x x, and returns the angle whose tangent is equal. Arc Tan Examples.
From www.storyofmathematics.com
arctan(0) Definition, Applications, and Examples Arc Tan Examples Given arctan() = θ, we can find that tan(θ) =. Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below.. Arc Tan Examples.
From www.inchcalculator.com
Inverse Tangent Calculator Calculate arctan(x) Inch Calculator Arc Tan Examples In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. In the right triangle, the base is 23 m and the height is. Tan (π / 3) = √3 ⇒.. Arc Tan Examples.
From www.youtube.com
Integral of x*arctan(x) (by parts) YouTube Arc Tan Examples In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. Given below are some examples that can help us understand how the arctan function works: Let’s look. Arc Tan Examples.
From www.geeksforgeeks.org
Arctan Formula, Graph, Identities, Domain, Range & FAQs Arc Tan Examples Let’s look at some examples to understand it more clearly. In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Here, we will study in detail. Arc Tan Examples.
From studylib.net
The Useful Arctan Integral Form Arc Tan Examples Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. In the right triangle, the base is 23 m and the height is. Given below are some examples that can help us understand how the arctan function works: The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. The. Arc Tan Examples.
From www.youtube.com
cot^1(x) = tan^1(1/x) arccot x = arctan(1/x) YouTube Arc Tan Examples Tan (π / 3) = √3 ⇒. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x. Also, we will learn the formulas, derivative, and integral of. Arc Tan Examples.
From www.youtube.com
Derivative of arctan x YouTube Arc Tan Examples Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. In the right triangle, the base is 23 m and the height is. Tan (π / 3) = √3 ⇒. Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. Also, we will learn the. Arc Tan Examples.
From www.youtube.com
Integral of arctan(x)/x^2 Integral example YouTube Arc Tan Examples In the right triangle, the base is 23 m and the height is. Tan (π / 3) = √3 ⇒. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. In other words, it helps us find the angle θ θ such that tan(θ) = x tan (θ) = x.. Arc Tan Examples.
From ar.inspiredpencil.com
Arctan Tan Inverse Arc Tan Examples Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. Arctan formula is used in solving various trigonometric problems and the same is explained in the example. Arc Tan Examples.
From en.neurochispas.com
Arctan Calculator (Inverse Tangent) Degrees and Radians Neurochispas Arc Tan Examples Tan (π / 2) = ∞ ⇒ arctan (∞) = π/2. Let’s look at some examples to understand it more clearly. Here, we will study in detail about the inverse tan function (arctan) along with its properties, graph, domain, and range. Arctan formula is used in solving various trigonometric problems and the same is explained in the example added below.. Arc Tan Examples.
From www.cuemath.com
Tangent Function Tan Graph Solved Examples Cuemath Arc Tan Examples Let’s look at some examples to understand it more clearly. The arctan function takes an input value, x x, and returns the angle whose tangent is equal to x x. The inverse trigonometric functions are the inverse functions of the \ (y=\sin x\), \ (y=\cos x\), and \ (y=\tan x\) functions restricted to. Given arctan() = θ, we can find. Arc Tan Examples.