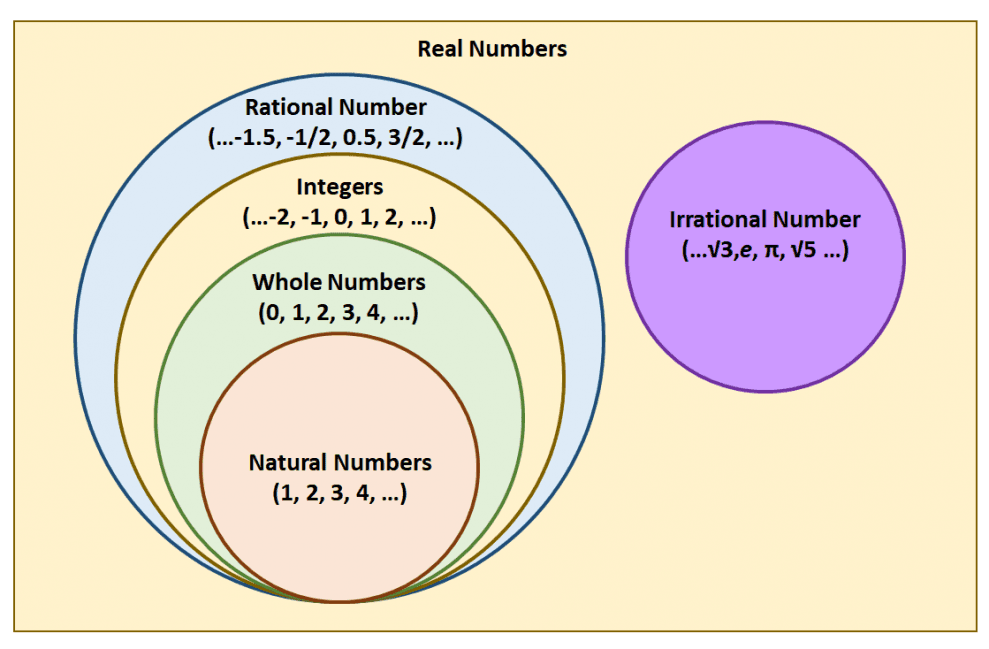
Is The Set Of Complex Numbers Closed Under Division at Edward Varley blog

Is The Set Of Complex Numbers Closed Under Division. $\forall z, w \in \c: The closure of $a$ , denoted $\overline{a}$ , is defined to be the smallest closed set. It does not make sense to ask if a set is closed under an operation when the operation is not defined for all pairs of elements. Apparently we don’t need to. Z + w \in \c$ complex addition is associative. For example, we can say that the integers are closed under multiplication as $$\forall a, b \in \mathbb{z}, \quad ab \in \mathbb{z}$$ while. One definition of the complex numbers is that they are the algebraic closure of the reals. Two complex numbers are equal if and only if their real parts and their imaginary parts are respectively equal. In other words, start with the reals and write down some. Let $a$ be a set of complex numbers. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. The set of complex numbers $\c$ is closed under addition:

$\forall z, w \in \c: One definition of the complex numbers is that they are the algebraic closure of the reals. Apparently we don’t need to. Z + w \in \c$ complex addition is associative. Let $a$ be a set of complex numbers. Two complex numbers are equal if and only if their real parts and their imaginary parts are respectively equal. For example, we can say that the integers are closed under multiplication as $$\forall a, b \in \mathbb{z}, \quad ab \in \mathbb{z}$$ while. The set of complex numbers $\c$ is closed under addition: The closure of $a$ , denoted $\overline{a}$ , is defined to be the smallest closed set. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication.

Closed Under Addition Property, Type of Numbers, and Examples The

Is The Set Of Complex Numbers Closed Under Division One definition of the complex numbers is that they are the algebraic closure of the reals. For example, we can say that the integers are closed under multiplication as $$\forall a, b \in \mathbb{z}, \quad ab \in \mathbb{z}$$ while. It does not make sense to ask if a set is closed under an operation when the operation is not defined for all pairs of elements. Z + w \in \c$ complex addition is associative. One definition of the complex numbers is that they are the algebraic closure of the reals. Apparently we don’t need to. The closure of $a$ , denoted $\overline{a}$ , is defined to be the smallest closed set. Two complex numbers are equal if and only if their real parts and their imaginary parts are respectively equal. Let $a$ be a set of complex numbers. Since the sum and product of complex numbers are complex numbers, we say that the complex numbers are closed under addition and multiplication. In other words, start with the reals and write down some. $\forall z, w \in \c: The set of complex numbers $\c$ is closed under addition: