Combination Examples Of Structures . Let us see a number of examples to get a firm grasp on the concept of combinations. How does this number change if. Combinations are selections of objects in a collection, in which the order of the selection does not matter. In all of these examples, sometimes we have to use permutation, other times we. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). Now we are ready to look at some mixed examples. In combinations, we can select the. By simply applying the definition of a binomial coefficient, definition. You have a bunch of chips which come in five different colors:
from mavink.com
From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). Now we are ready to look at some mixed examples. Combinations are selections of objects in a collection, in which the order of the selection does not matter. You have a bunch of chips which come in five different colors: By simply applying the definition of a binomial coefficient, definition. How does this number change if. In all of these examples, sometimes we have to use permutation, other times we. In combinations, we can select the. Let us see a number of examples to get a firm grasp on the concept of combinations.
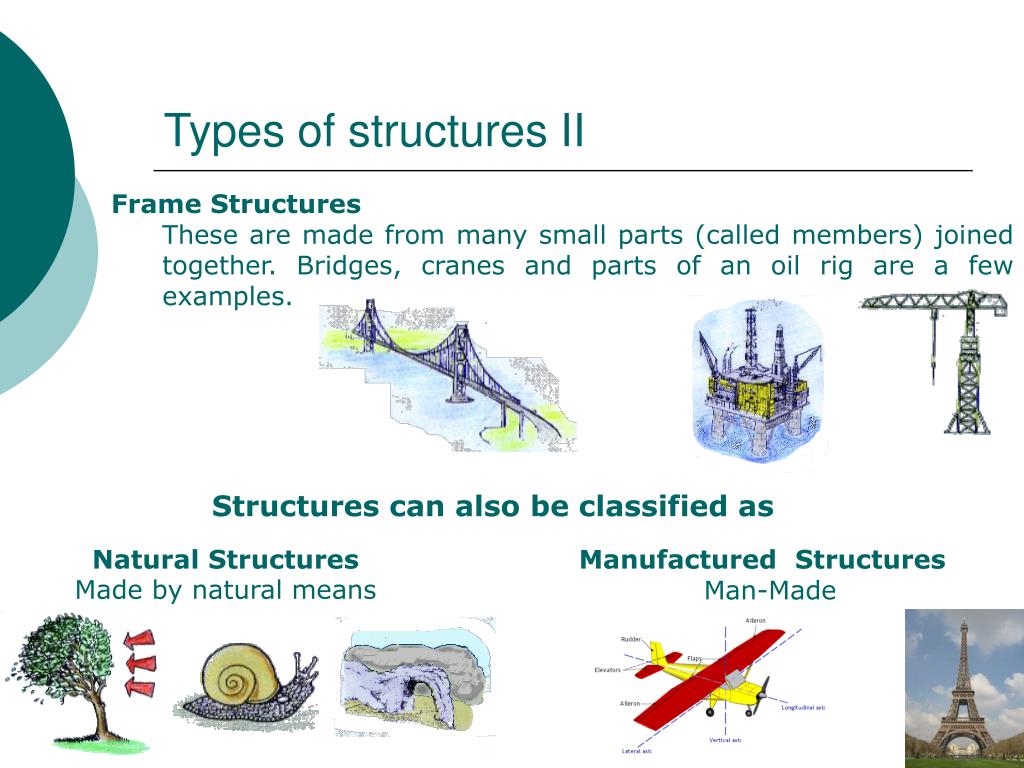
What Are Different Types Of Structures
Combination Examples Of Structures Now we are ready to look at some mixed examples. You have a bunch of chips which come in five different colors: In combinations, we can select the. Now we are ready to look at some mixed examples. Let us see a number of examples to get a firm grasp on the concept of combinations. In all of these examples, sometimes we have to use permutation, other times we. Combinations are selections of objects in a collection, in which the order of the selection does not matter. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). By simply applying the definition of a binomial coefficient, definition. How does this number change if.
From www.slideserve.com
PPT Competitions Tournament Formats PowerPoint Presentation ID2066385 Combination Examples Of Structures From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). Now we are ready to look at some mixed examples. You have a bunch of chips which come in five different colors: Let us see a number of examples to get a firm grasp on the concept of. Combination Examples Of Structures.
From www.structuralbasics.com
What Are Load Combinations And How To Calculate Them? Structural Basics Combination Examples Of Structures How does this number change if. Let us see a number of examples to get a firm grasp on the concept of combinations. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). Now we are ready to look at some mixed examples. By simply applying the definition. Combination Examples Of Structures.
From theconstructor.org
What are the Types of Frame Structures? The Constructor Combination Examples Of Structures In combinations, we can select the. Now we are ready to look at some mixed examples. By simply applying the definition of a binomial coefficient, definition. You have a bunch of chips which come in five different colors: Combinations are selections of objects in a collection, in which the order of the selection does not matter. From the example above,. Combination Examples Of Structures.
From slideplayer.com
Structures What do we understand when we talk about structures in Combination Examples Of Structures Now we are ready to look at some mixed examples. In all of these examples, sometimes we have to use permutation, other times we. You have a bunch of chips which come in five different colors: From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). How does. Combination Examples Of Structures.
From resumegenius.com
Combination Resume Free Template & Examples Combination Examples Of Structures Combinations are selections of objects in a collection, in which the order of the selection does not matter. In all of these examples, sometimes we have to use permutation, other times we. In combinations, we can select the. You have a bunch of chips which come in five different colors: By simply applying the definition of a binomial coefficient, definition.. Combination Examples Of Structures.
From leah4sci.com
Naming Ethers Tutorial Video by Leah4sci using IUPAC and common naming Combination Examples Of Structures From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). By simply applying the definition of a binomial coefficient, definition. Now we are ready to look at some mixed examples. How does this number change if. Let us see a number of examples to get a firm grasp. Combination Examples Of Structures.
From www.youtube.com
Combination Example Problem YouTube Combination Examples Of Structures By simply applying the definition of a binomial coefficient, definition. Now we are ready to look at some mixed examples. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). You have a bunch of chips which come in five different colors: In combinations, we can select the.. Combination Examples Of Structures.
From printablelibfigures.z19.web.core.windows.net
How To Do Combinations Math Combination Examples Of Structures You have a bunch of chips which come in five different colors: By simply applying the definition of a binomial coefficient, definition. Combinations are selections of objects in a collection, in which the order of the selection does not matter. How does this number change if. In combinations, we can select the. Let us see a number of examples to. Combination Examples Of Structures.
From www.youtube.com
Introduction to Eurocode 0 EC0 EN1990 Basis of Structural Design Combination Examples Of Structures Combinations are selections of objects in a collection, in which the order of the selection does not matter. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). In all of these examples, sometimes we have to use permutation, other times we. In combinations, we can select the.. Combination Examples Of Structures.
From mavink.com
What Are Different Types Of Structures Combination Examples Of Structures You have a bunch of chips which come in five different colors: In combinations, we can select the. How does this number change if. Combinations are selections of objects in a collection, in which the order of the selection does not matter. In all of these examples, sometimes we have to use permutation, other times we. By simply applying the. Combination Examples Of Structures.
From civiljungle.com
What Is Shell Structure 11 Types of Shell Structure Applications Combination Examples Of Structures In combinations, we can select the. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). Now we are ready to look at some mixed examples. In all of these examples, sometimes we have to use permutation, other times we. You have a bunch of chips which come. Combination Examples Of Structures.
From thebrucezone.weebly.com
1 Understanding Structures the BRUCE Zone Combination Examples Of Structures From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). You have a bunch of chips which come in five different colors: In all of these examples, sometimes we have to use permutation, other times we. Let us see a number of examples to get a firm grasp. Combination Examples Of Structures.
From biologynotesonline.com
Biological Macromolecules Types, Structure, Functions, Examples Combination Examples Of Structures By simply applying the definition of a binomial coefficient, definition. You have a bunch of chips which come in five different colors: Combinations are selections of objects in a collection, in which the order of the selection does not matter. In combinations, we can select the. In all of these examples, sometimes we have to use permutation, other times we.. Combination Examples Of Structures.
From tainguyenmienphi.com
[SHARE] JavaScript Data Structures & Algorithms + LEETCODE Exercises Combination Examples Of Structures By simply applying the definition of a binomial coefficient, definition. You have a bunch of chips which come in five different colors: How does this number change if. In combinations, we can select the. Let us see a number of examples to get a firm grasp on the concept of combinations. In all of these examples, sometimes we have to. Combination Examples Of Structures.
From www.slideserve.com
PPT Permutations and Combinations PowerPoint Presentation, free Combination Examples Of Structures By simply applying the definition of a binomial coefficient, definition. How does this number change if. In all of these examples, sometimes we have to use permutation, other times we. Now we are ready to look at some mixed examples. Let us see a number of examples to get a firm grasp on the concept of combinations. You have a. Combination Examples Of Structures.
From www.youtube.com
Understanding Combinations! YouTube Combination Examples Of Structures By simply applying the definition of a binomial coefficient, definition. Now we are ready to look at some mixed examples. In combinations, we can select the. Let us see a number of examples to get a firm grasp on the concept of combinations. How does this number change if. From the example above, we see that to compute \(p(n,k)\) we. Combination Examples Of Structures.
From engineeringdiscoveries.com
Types Of Structural Members Engineering Discoveries Combination Examples Of Structures How does this number change if. Now we are ready to look at some mixed examples. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). In combinations, we can select the. In all of these examples, sometimes we have to use permutation, other times we. Let us. Combination Examples Of Structures.
From www.youtube.com
Combinations Example 1 YouTube Combination Examples Of Structures Let us see a number of examples to get a firm grasp on the concept of combinations. Combinations are selections of objects in a collection, in which the order of the selection does not matter. You have a bunch of chips which come in five different colors: From the example above, we see that to compute \(p(n,k)\) we must apply. Combination Examples Of Structures.
From www.slideserve.com
PPT Chapter 10 PowerPoint Presentation, free download ID6076902 Combination Examples Of Structures Let us see a number of examples to get a firm grasp on the concept of combinations. Now we are ready to look at some mixed examples. By simply applying the definition of a binomial coefficient, definition. You have a bunch of chips which come in five different colors: In all of these examples, sometimes we have to use permutation,. Combination Examples Of Structures.
From www.pinterest.com
Linear Combination Explanation Math tutorials, Math tricks, Study Combination Examples Of Structures You have a bunch of chips which come in five different colors: Combinations are selections of objects in a collection, in which the order of the selection does not matter. By simply applying the definition of a binomial coefficient, definition. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting. Combination Examples Of Structures.
From exowzrafe.blob.core.windows.net
Combination Examples In Science at Brad Dixson blog Combination Examples Of Structures How does this number change if. Combinations are selections of objects in a collection, in which the order of the selection does not matter. By simply applying the definition of a binomial coefficient, definition. In all of these examples, sometimes we have to use permutation, other times we. From the example above, we see that to compute \(p(n,k)\) we must. Combination Examples Of Structures.
From criticalthinking.cloud
solving combination problems Combination Examples Of Structures You have a bunch of chips which come in five different colors: By simply applying the definition of a binomial coefficient, definition. Combinations are selections of objects in a collection, in which the order of the selection does not matter. Let us see a number of examples to get a firm grasp on the concept of combinations. In combinations, we. Combination Examples Of Structures.
From www.difference101.com
Permutation vs. Combination 4 Key Differences, Pros & Cons Combination Examples Of Structures Let us see a number of examples to get a firm grasp on the concept of combinations. In combinations, we can select the. Combinations are selections of objects in a collection, in which the order of the selection does not matter. How does this number change if. By simply applying the definition of a binomial coefficient, definition. Now we are. Combination Examples Of Structures.
From worksheetlibsmugged.z13.web.core.windows.net
Give An Example Of Combination Combination Examples Of Structures From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). In all of these examples, sometimes we have to use permutation, other times we. You have a bunch of chips which come in five different colors: Combinations are selections of objects in a collection, in which the order. Combination Examples Of Structures.
From www.researchgate.net
Combination of basic structures at level 3. Download Scientific Diagram Combination Examples Of Structures Combinations are selections of objects in a collection, in which the order of the selection does not matter. How does this number change if. By simply applying the definition of a binomial coefficient, definition. Now we are ready to look at some mixed examples. In all of these examples, sometimes we have to use permutation, other times we. Let us. Combination Examples Of Structures.
From www.slideserve.com
PPT Classifying Chemical Reactions PowerPoint Presentation, free Combination Examples Of Structures You have a bunch of chips which come in five different colors: Let us see a number of examples to get a firm grasp on the concept of combinations. In combinations, we can select the. By simply applying the definition of a binomial coefficient, definition. Now we are ready to look at some mixed examples. How does this number change. Combination Examples Of Structures.
From www.slideserve.com
PPT Permutations and Combinations PowerPoint Presentation, free Combination Examples Of Structures From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). By simply applying the definition of a binomial coefficient, definition. Now we are ready to look at some mixed examples. In all of these examples, sometimes we have to use permutation, other times we. In combinations, we can. Combination Examples Of Structures.
From fourweekmba.com
Matrix Organizational Structure In A Nutshell FourWeekMBA Combination Examples Of Structures In all of these examples, sometimes we have to use permutation, other times we. By simply applying the definition of a binomial coefficient, definition. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). In combinations, we can select the. Combinations are selections of objects in a collection,. Combination Examples Of Structures.
From webframes.org
Concrete Frame Structure Advantages And Disadvantages Combination Examples Of Structures By simply applying the definition of a binomial coefficient, definition. How does this number change if. Let us see a number of examples to get a firm grasp on the concept of combinations. Now we are ready to look at some mixed examples. In combinations, we can select the. Combinations are selections of objects in a collection, in which the. Combination Examples Of Structures.
From novoresume.com
Resume Structure & Formatting Guide [Get Hired in 2024] Combination Examples Of Structures Now we are ready to look at some mixed examples. Let us see a number of examples to get a firm grasp on the concept of combinations. By simply applying the definition of a binomial coefficient, definition. In all of these examples, sometimes we have to use permutation, other times we. Combinations are selections of objects in a collection, in. Combination Examples Of Structures.
From www.youtube.com
ULS Load Combinations Example YouTube Combination Examples Of Structures Combinations are selections of objects in a collection, in which the order of the selection does not matter. How does this number change if. Let us see a number of examples to get a firm grasp on the concept of combinations. Now we are ready to look at some mixed examples. By simply applying the definition of a binomial coefficient,. Combination Examples Of Structures.
From logicxonomy.com
Permutation And Combination Class 11 (Powerful Formula And Updated Tips Combination Examples Of Structures Combinations are selections of objects in a collection, in which the order of the selection does not matter. In combinations, we can select the. By simply applying the definition of a binomial coefficient, definition. In all of these examples, sometimes we have to use permutation, other times we. You have a bunch of chips which come in five different colors:. Combination Examples Of Structures.
From dxobmcfxr.blob.core.windows.net
How To Find N In Combination Formula at Alicia Ford blog Combination Examples Of Structures By simply applying the definition of a binomial coefficient, definition. You have a bunch of chips which come in five different colors: In combinations, we can select the. From the example above, we see that to compute \(p(n,k)\) we must apply the multiplicative principle to \(k\) numbers, starting with \(n\). Now we are ready to look at some mixed examples.. Combination Examples Of Structures.
From www.qualitygurus.com
Permutations and Combination Quality Gurus Combination Examples Of Structures In all of these examples, sometimes we have to use permutation, other times we. Now we are ready to look at some mixed examples. How does this number change if. Let us see a number of examples to get a firm grasp on the concept of combinations. By simply applying the definition of a binomial coefficient, definition. From the example. Combination Examples Of Structures.
From webframes.org
Strengthening Frame Structures Combination Examples Of Structures You have a bunch of chips which come in five different colors: By simply applying the definition of a binomial coefficient, definition. How does this number change if. Let us see a number of examples to get a firm grasp on the concept of combinations. Now we are ready to look at some mixed examples. From the example above, we. Combination Examples Of Structures.