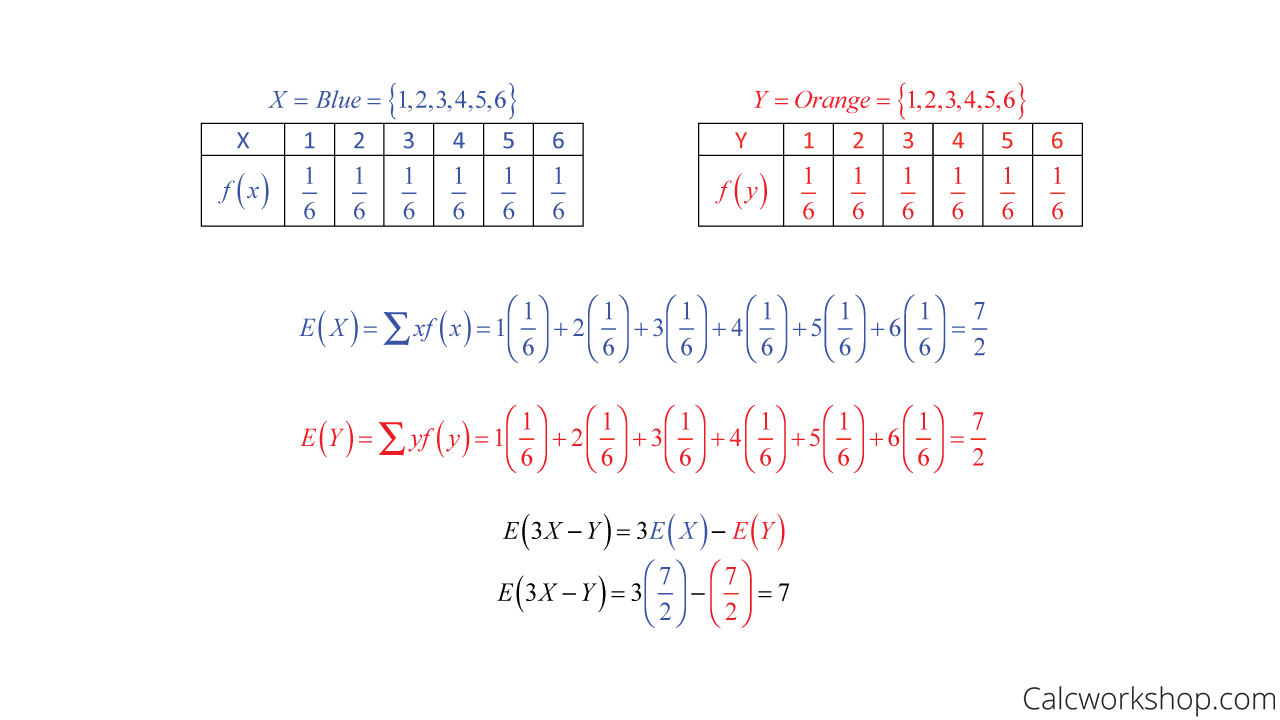Linear Combination Examples Numbers . Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. Linear combinations of a single vector \(\mathbf{v}\) are thus just. In this section, we have found an especially simple way to express linear systems using matrix multiplication. This example demonstrates the connection between linear combinations and linear systems. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. I did so using the euclidean. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. I was told to find the gcd of 34 and 126. I am working on gcd's in my algebraic structures class. Asking if a vector \(\mathbf b\) is a linear. How to take linear combinations of matrices and vectors. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\).
from calcworkshop.com
Linear combinations of a single vector \(\mathbf{v}\) are thus just. In this section, we have found an especially simple way to express linear systems using matrix multiplication. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. This example demonstrates the connection between linear combinations and linear systems. How to take linear combinations of matrices and vectors. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. Asking if a vector \(\mathbf b\) is a linear. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. I was told to find the gcd of 34 and 126.
Linear Combination of Random Variables (w/ 9 Examples!)
Linear Combination Examples Numbers Linear combinations of a single vector \(\mathbf{v}\) are thus just. I was told to find the gcd of 34 and 126. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). How to take linear combinations of matrices and vectors. Linear combinations of a single vector \(\mathbf{v}\) are thus just. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. I did so using the euclidean. In this section, we have found an especially simple way to express linear systems using matrix multiplication. I am working on gcd's in my algebraic structures class. Asking if a vector \(\mathbf b\) is a linear. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. This example demonstrates the connection between linear combinations and linear systems. Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then.
From www.slideserve.com
PPT The Laws of Linear Combination PowerPoint Presentation, free Linear Combination Examples Numbers Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. This example demonstrates the connection between linear combinations and linear systems. Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. I am working on gcd's in my algebraic structures class. How to take linear combinations of matrices and vectors.. Linear Combination Examples Numbers.
From www.youtube.com
Determine if b is a linear combination of vectors formed from the Linear Combination Examples Numbers Linear combinations of a single vector \(\mathbf{v}\) are thus just. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. In this section, we have found an especially simple way to express linear systems using matrix multiplication. I was told to find the gcd of 34 and 126. Linear combination involves combining. Linear Combination Examples Numbers.
From www.youtube.com
Intro to Linear Combinations YouTube Linear Combination Examples Numbers This example demonstrates the connection between linear combinations and linear systems. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). Linear combinations of a single vector \(\mathbf{v}\) are thus just. I am working on gcd's in my algebraic structures class. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. How to take linear combinations of matrices and vectors. A linear. Linear Combination Examples Numbers.
From www.slideserve.com
PPT The Laws of Linear Combination PowerPoint Presentation, free Linear Combination Examples Numbers I was told to find the gcd of 34 and 126. This example demonstrates the connection between linear combinations and linear systems. Linear combinations of a single vector \(\mathbf{v}\) are thus just. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. In this section, we have found an especially simple way. Linear Combination Examples Numbers.
From www.youtube.com
L13 Linear Combination Example of L C Linear Algebra Vector Linear Combination Examples Numbers I was told to find the gcd of 34 and 126. In this section, we have found an especially simple way to express linear systems using matrix multiplication. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. I am working on gcd's in my algebraic structures class. I did so using. Linear Combination Examples Numbers.
From www.slideserve.com
PPT Number Theory and Cryptography PowerPoint Presentation, free Linear Combination Examples Numbers Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. Linear combinations of a single vector \(\mathbf{v}\) are thus just. I did so using the euclidean. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. I was told to find the gcd of 34 and 126. In this section, we have. Linear Combination Examples Numbers.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Examples Numbers How to take linear combinations of matrices and vectors. Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). I am working on gcd's in my algebraic structures class. Asking if a vector \(\mathbf b\) is a linear. This example demonstrates the. Linear Combination Examples Numbers.
From gioriacxm.blob.core.windows.net
Linear Combination Meaning Maths at Barbara Henderson blog Linear Combination Examples Numbers A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. This example demonstrates the connection between linear combinations and linear systems. Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. Asking if a vector \(\mathbf b\) is a linear. In this. Linear Combination Examples Numbers.
From www.slideserve.com
PPT Linear Constantcoefficient Difference Equations PowerPoint Linear Combination Examples Numbers I did so using the euclidean. In this section, we have found an especially simple way to express linear systems using matrix multiplication. How to take linear combinations of matrices and vectors. I am working on gcd's in my algebraic structures class. Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number). Linear Combination Examples Numbers.
From www.slideserve.com
PPT The Laws of Linear Combination PowerPoint Presentation, free Linear Combination Examples Numbers I did so using the euclidean. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Asking if a vector \(\mathbf b\) is a linear. This example demonstrates the connection between linear combinations and linear systems. In this section, we have found an especially simple way to express linear systems using matrix. Linear Combination Examples Numbers.
From www.youtube.com
Solving Systems Using Linear Combination (Simplifying Math) YouTube Linear Combination Examples Numbers I was told to find the gcd of 34 and 126. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Linear combinations of a single vector \(\mathbf{v}\) are thus just. I did so using the euclidean. This example demonstrates the connection between linear combinations and linear systems. Asking if a vector. Linear Combination Examples Numbers.
From www.youtube.com
Linear Combination of Multiple Random Variables Example YouTube Linear Combination Examples Numbers Linear combinations of a single vector \(\mathbf{v}\) are thus just. I am working on gcd's in my algebraic structures class. How to take linear combinations of matrices and vectors. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. This example demonstrates the connection between linear combinations and linear systems. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). In this. Linear Combination Examples Numbers.
From www.youtube.com
Find gcd and Express gcd as linear combination Number Theory Linear Combination Examples Numbers I did so using the euclidean. This example demonstrates the connection between linear combinations and linear systems. Asking if a vector \(\mathbf b\) is a linear. I am working on gcd's in my algebraic structures class. Linear combinations of a single vector \(\mathbf{v}\) are thus just. Linear combination involves combining a set of vectors by multiplying each vector by a. Linear Combination Examples Numbers.
From tr.pinterest.com
Linear Combination Explanation Math tutorials, Math tricks, Study Linear Combination Examples Numbers A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. In this section, we have found an especially simple way to express. Linear Combination Examples Numbers.
From www.youtube.com
Number Theory 27 Linear Combination Example and a Theorem YouTube Linear Combination Examples Numbers Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. I am working on gcd's in my algebraic structures class. Linear combinations of a single vector \(\mathbf{v}\) are thus just. I did so using the euclidean. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. Asking if a vector. Linear Combination Examples Numbers.
From www.algebra-class.com
Solving Systems of Equations Using Linear Combinations Linear Combination Examples Numbers In this section, we have found an especially simple way to express linear systems using matrix multiplication. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). Linear combinations of a single vector \(\mathbf{v}\) are thus just. This example demonstrates the connection between linear combinations and linear systems. How to take linear combinations of matrices and vectors. Asking if a vector \(\mathbf. Linear Combination Examples Numbers.
From gioriacxm.blob.core.windows.net
Linear Combination Meaning Maths at Barbara Henderson blog Linear Combination Examples Numbers Asking if a vector \(\mathbf b\) is a linear. I was told to find the gcd of 34 and 126. In this section, we have found an especially simple way to express linear systems using matrix multiplication. How to take linear combinations of matrices and vectors. Linear combination involves combining a set of vectors by multiplying each vector by a. Linear Combination Examples Numbers.
From www.youtube.com
vector equations linear combinations YouTube Linear Combination Examples Numbers Linear combinations of a single vector \(\mathbf{v}\) are thus just. Asking if a vector \(\mathbf b\) is a linear. Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. How to take linear combinations of matrices and vectors. This example demonstrates the connection between linear combinations and linear systems. I. Linear Combination Examples Numbers.
From heung-bae-lee.github.io
Linear combination, vector equation, Four views of matrix Linear Combination Examples Numbers Asking if a vector \(\mathbf b\) is a linear. Linear combinations of a single vector \(\mathbf{v}\) are thus just. In this section, we have found an especially simple way to express linear systems using matrix multiplication. I am working on gcd's in my algebraic structures class. Linear combination involves combining a set of vectors by multiplying each vector by a. Linear Combination Examples Numbers.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Examples Numbers This example demonstrates the connection between linear combinations and linear systems. Asking if a vector \(\mathbf b\) is a linear. Linear combinations of a single vector \(\mathbf{v}\) are thus just. I did so using the euclidean. I am working on gcd's in my algebraic structures class. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). A linear combination of a vector. Linear Combination Examples Numbers.
From www.numerade.com
SOLVED Using the linear combination method what is the solution to the Linear Combination Examples Numbers Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. I did so using the euclidean. I am working on gcd's in my algebraic structures class. Asking if a vector \(\mathbf b\) is a linear. Linear combinations of a single vector \(\mathbf{v}\). Linear Combination Examples Numbers.
From www.wikihow.com
5 Ways to Solve Systems Using Linear Combinations wikiHow Linear Combination Examples Numbers Linear combinations of a single vector \(\mathbf{v}\) are thus just. How to take linear combinations of matrices and vectors. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Asking if a vector \(\mathbf b\) is a linear. I was told to find the gcd of 34 and 126. In this section,. Linear Combination Examples Numbers.
From www.slideserve.com
PPT The Laws of Linear Combination PowerPoint Presentation, free Linear Combination Examples Numbers Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. This example demonstrates the connection between linear combinations and linear systems. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. I am working on gcd's in my algebraic structures class. Linear combinations of a single vector \(\mathbf{v}\) are thus. Linear Combination Examples Numbers.
From www.slideserve.com
PPT ENGG2013 Unit 5 Linear Combination & Linear Independence Linear Combination Examples Numbers I am working on gcd's in my algebraic structures class. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. I did so using the euclidean. In this section, we have found an especially. Linear Combination Examples Numbers.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Examples Numbers Linear combination involves combining a set of vectors by multiplying each vector by a scalar (a real number) and then. I was told to find the gcd of 34 and 126. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. Let. Linear Combination Examples Numbers.
From www.youtube.com
Writing gcd as a linear combination using Euclidean Algorithm YouTube Linear Combination Examples Numbers In this section, we have found an especially simple way to express linear systems using matrix multiplication. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). I did so using the euclidean. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. Linear combinations of a single vector \(\mathbf{v}\) are thus just. How to take linear combinations of matrices and vectors.. Linear Combination Examples Numbers.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Linear Combination Examples Numbers I did so using the euclidean. This example demonstrates the connection between linear combinations and linear systems. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. I am working on gcd's in my algebraic structures class. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. In this section, we have. Linear Combination Examples Numbers.
From heung-bae-lee.github.io
Linear combination, vector equation, Four views of matrix Linear Combination Examples Numbers A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. How to take linear combinations of matrices and vectors. I am working on gcd's in my algebraic structures class. Linear combination involves combining a set of vectors by multiplying each vector by. Linear Combination Examples Numbers.
From www.youtube.com
Linear Algebra 124, Linear Combination, examples YouTube Linear Combination Examples Numbers How to take linear combinations of matrices and vectors. I am working on gcd's in my algebraic structures class. Linear combinations of a single vector \(\mathbf{v}\) are thus just. Asking if a vector \(\mathbf b\) is a linear. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). Linear combination involves combining a set of vectors by multiplying each vector by a. Linear Combination Examples Numbers.
From www.youtube.com
Linear Combination Definition Examples Revision Lecture 3 YouTube Linear Combination Examples Numbers I am working on gcd's in my algebraic structures class. I did so using the euclidean. Asking if a vector \(\mathbf b\) is a linear. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. This example demonstrates the connection between linear combinations and linear systems. Linear combination involves combining a set. Linear Combination Examples Numbers.
From www.slideserve.com
PPT Linear Constantcoefficient Difference Equations PowerPoint Linear Combination Examples Numbers A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. This example demonstrates the connection between linear combinations and linear systems. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. I am working on gcd's in my algebraic structures class. In this section, we have found an especially simple way to. Linear Combination Examples Numbers.
From www.slideserve.com
PPT The Laws of Linear Combination PowerPoint Presentation, free Linear Combination Examples Numbers Linear combinations of a single vector \(\mathbf{v}\) are thus just. I am working on gcd's in my algebraic structures class. I did so using the euclidean. How to take linear combinations of matrices and vectors. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. Any expression of the form \[ x_1. Linear Combination Examples Numbers.
From www.youtube.com
Solving Systems of Linear Equations Linear Combination Method YouTube Linear Combination Examples Numbers Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. Let \(\vect{v}_1, \ldots, \vect{v}_n\) be vectors in \(\mathbb{r}^m\). I am working on gcd's in my algebraic structures class. This example demonstrates the connection between linear combinations and linear systems. Asking if a vector \(\mathbf b\) is a linear. I did so using the euclidean. In this section, we have found. Linear Combination Examples Numbers.
From www.algebra-class.com
Solving Systems of Equations Using Linear Combinations Linear Combination Examples Numbers I am working on gcd's in my algebraic structures class. I was told to find the gcd of 34 and 126. I did so using the euclidean. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where \(x\) is some real number. This example demonstrates the connection between linear combinations and linear systems. How to take linear. Linear Combination Examples Numbers.
From www.youtube.com
(Abstract Algebra 1) Linear Combinations YouTube Linear Combination Examples Numbers How to take linear combinations of matrices and vectors. In this section, we have found an especially simple way to express linear systems using matrix multiplication. This example demonstrates the connection between linear combinations and linear systems. Any expression of the form \[ x_1 \vect{v}_1+\cdots+x_n \vect{v}_n,\nonumber\] where. A linear combination of a vector \(\mathbf{v}\) is of the form \(x\mathbf{v}\), where. Linear Combination Examples Numbers.