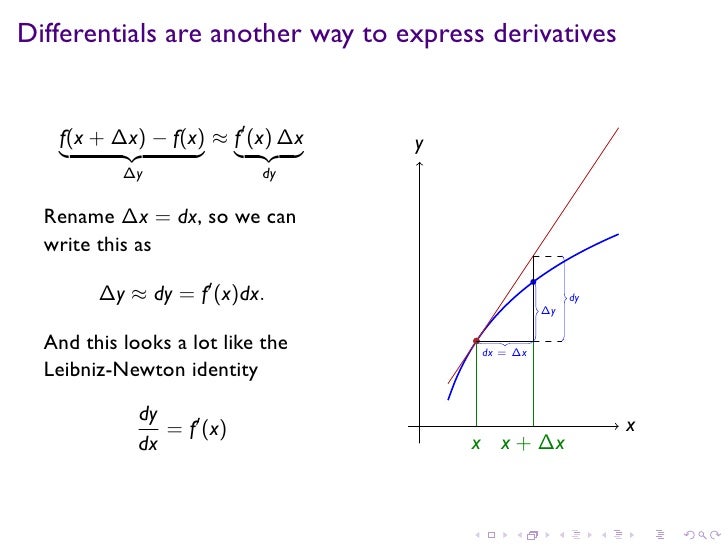
Differentials Linear Approximation Formula . Determine the equation of a plane tangent to a given surface at a point. Describe the linear approximation to a function at a point. Use the tangent plane to approximate a function of two variables at a point. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. As long as the change dx in input x is. 4.2.1 describe the linear approximation to a function at a point. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. 4.2.2 write the linearization of a given function. Write the linearization of a given function. The basic formula for linear approximation is: F(x) = f(a) ' + f (a)(x − a) here. Draw a graph that illustrates the use of differentials to approximate the change in a. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point.
from www.slideshare.net
Write the linearization of a given function. Describe the linear approximation to a function at a point. Describe the linear approximation to a function at a point. 4.2.2 write the linearization of a given function. As long as the change dx in input x is. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. F(x) = f(a) ' + f (a)(x − a) here. Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.1 describe the linear approximation to a function at a point. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =.
Lesson 13 Linear Approximation
Differentials Linear Approximation Formula 4.2.1 describe the linear approximation to a function at a point. As long as the change dx in input x is. F(x) = f(a) ' + f (a)(x − a) here. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. Use the tangent plane to approximate a function of two variables at a point. Describe the linear approximation to a function at a point. Write the linearization of a given function. Determine the equation of a plane tangent to a given surface at a point. Describe the linear approximation to a function at a point. Write the linearization of a given function. The basic formula for linear approximation is: Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.1 describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.2 write the linearization of a given function.
From calcworkshop.com
Linear Approximation (How To w/ StepbyStep Examples!) Differentials Linear Approximation Formula As long as the change dx in input x is. Determine the equation of a plane tangent to a given surface at a point. Describe the linear approximation to a function at a point. Use the tangent plane to approximate a function of two variables at a point. Write the linearization of a given function. The resulting linear approximation of. Differentials Linear Approximation Formula.
From www.studypug.com
Understanding linear approximation in calculus StudyPug Differentials Linear Approximation Formula Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Draw a graph that illustrates the use of differentials to approximate the change in a. Draw a graph that illustrates the use of differentials to approximate the change in a. Write the linearization. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula Describe the linear approximation to a function at a point. Determine the equation of a plane tangent to a given surface at a point. F(x) = f(a) ' + f (a)(x − a) here. Use the tangent plane to approximate a function of two variables at a point. Draw a graph that illustrates the use of differentials to approximate the. Differentials Linear Approximation Formula.
From www.youtube.com
Use linear approximation to estimate Differential Calculus YouTube Differentials Linear Approximation Formula Determine the equation of a plane tangent to a given surface at a point. 4.2.2 write the linearization of a given function. Write the linearization of a given function. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Differentials are useful when the value of a quantity is. Differentials Linear Approximation Formula.
From www.slideserve.com
PPT Linear approximation and differentials ( Section 3.9) PowerPoint Differentials Linear Approximation Formula As long as the change dx in input x is. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Write the linearization of a given function. Use the tangent plane to approximate a function of two variables at a point. Describe the linear approximation to a function at. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula 4.2.1 describe the linear approximation to a function at a point. Use the tangent plane to approximate a function of two variables at a point. Draw a graph that illustrates the use of differentials to approximate the change in a. Determine the equation of a plane tangent to a given surface at a point. Write the linearization of a given. Differentials Linear Approximation Formula.
From www.teachoo.com
Question 9 Use differential to approximate (25)1/3 Examples Differentials Linear Approximation Formula The basic formula for linear approximation is: F(x) = f(a) ' + f (a)(x − a) here. Write the linearization of a given function. Determine the equation of a plane tangent to a given surface at a point. 4.2.1 describe the linear approximation to a function at a point. Use the tangent plane to approximate a function of two variables. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula Draw a graph that illustrates the use of differentials to approximate the change in a. Determine the equation of a plane tangent to a given surface at a point. Write the linearization of a given function. As long as the change dx in input x is. 4.2.2 write the linearization of a given function. Draw a graph that illustrates the. Differentials Linear Approximation Formula.
From www.youtube.com
Approximation Using Differentials YouTube Differentials Linear Approximation Formula 4.2.2 write the linearization of a given function. Determine the equation of a plane tangent to a given surface at a point. The basic formula for linear approximation is: The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. 4.2.1 describe the linear approximation to a function at a. Differentials Linear Approximation Formula.
From www.slideserve.com
PPT 4.5 Linear Approximations, Differentials and Newton’s Method Differentials Linear Approximation Formula 4.2.1 describe the linear approximation to a function at a point. Write the linearization of a given function. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Draw a graph that illustrates the use of differentials to approximate the change in a.. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Draw a graph that illustrates the use of differentials to approximate the change in a. Determine the equation of a plane tangent to a given surface at a point. The basic formula for linear approximation is: F(x) = f(a). Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Determine the equation of a plane tangent to a given surface at a point. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. As long as the change dx. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula Describe the linear approximation to a function at a point. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. 4.2.2 write the linearization. Differentials Linear Approximation Formula.
From www.slideshare.net
Lesson 13 Linear Approximation Differentials Linear Approximation Formula Draw a graph that illustrates the use of differentials to approximate the change in a. The basic formula for linear approximation is: F(x) = f(a) ' + f (a)(x − a) here. 4.2.1 describe the linear approximation to a function at a point. Write the linearization of a given function. As long as the change dx in input x is.. Differentials Linear Approximation Formula.
From www.coursehero.com
[Solved] Use a linear approximation (or differentials) to estimate the Differentials Linear Approximation Formula Draw a graph that illustrates the use of differentials to approximate the change in a. F(x) = f(a) ' + f (a)(x − a) here. Write the linearization of a given function. 4.2.2 write the linearization of a given function. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response. Differentials Linear Approximation Formula.
From www.slideserve.com
PPT Linear Approximation and Differentials PowerPoint Presentation Differentials Linear Approximation Formula The basic formula for linear approximation is: Draw a graph that illustrates the use of differentials to approximate the change in a. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Describe the linear approximation to a function at a point. Draw. Differentials Linear Approximation Formula.
From slideplayer.com
§3.10 Linear Approximations and Differentials ppt download Differentials Linear Approximation Formula 4.2.2 write the linearization of a given function. As long as the change dx in input x is. The basic formula for linear approximation is: The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. A = 64 and f(x) = x3 , so f(a) = f(64) = 4. Differentials Linear Approximation Formula.
From solvedlib.com
2 _ Use linear approximation (differentials) of the f… SolvedLib Differentials Linear Approximation Formula Write the linearization of a given function. Write the linearization of a given function. F(x) = f(a) ' + f (a)(x − a) here. Determine the equation of a plane tangent to a given surface at a point. Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a. Differentials Linear Approximation Formula.
From educationcareeronline.com
Linear Approximation Formula & Example Education Career Differentials Linear Approximation Formula The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Write the linearization of a given function. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. Describe the linear approximation to a function at a point. 4.2.2 write the. Differentials Linear Approximation Formula.
From www.slideserve.com
PPT Section 3.9 Differentials PowerPoint Presentation, free Differentials Linear Approximation Formula The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Use the tangent plane to approximate a function of two variables at a point. 4.2.2 write the linearization of a given function. 4.2.1 describe the linear approximation to a function at a point. Determine the equation of a plane. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula Write the linearization of a given function. Describe the linear approximation to a function at a point. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. 4.2.2 write the linearization of a given function. Differentials are useful when the value of a quantity is unimportant, only the approximate change in. Differentials Linear Approximation Formula.
From www.studocu.com
Linear Approximations and Differentials f x s I find the equation of Differentials Linear Approximation Formula 4.2.1 describe the linear approximation to a function at a point. Describe the linear approximation to a function at a point. Write the linearization of a given function. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. Differentials are useful when the value of a quantity is unimportant, only the. Differentials Linear Approximation Formula.
From www.youtube.com
Linear Approximation Using Differentials YouTube Differentials Linear Approximation Formula Describe the linear approximation to a function at a point. 4.2.2 write the linearization of a given function. The basic formula for linear approximation is: A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. 4.2.1 describe the linear approximation to a function at a point. Describe the linear approximation to. Differentials Linear Approximation Formula.
From www.slideserve.com
PPT Linear approximation and differentials ( Section 3.9) PowerPoint Differentials Linear Approximation Formula A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. 4.2.2 write the linearization of a given function. Describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.1 describe the linear approximation to a function. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. Describe the linear approximation to a function at a point. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Determine the equation of a plane tangent to a given. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula F(x) = f(a) ' + f (a)(x − a) here. Describe the linear approximation to a function at a point. Write the linearization of a given function. 4.2.2 write the linearization of a given function. Describe the linear approximation to a function at a point. 4.2.1 describe the linear approximation to a function at a point. As long as the. Differentials Linear Approximation Formula.
From www.slideserve.com
PPT Linear approximation and differentials ( Section 3.9) PowerPoint Differentials Linear Approximation Formula Determine the equation of a plane tangent to a given surface at a point. The basic formula for linear approximation is: F(x) = f(a) ' + f (a)(x − a) here. Describe the linear approximation to a function at a point. Write the linearization of a given function. A = 64 and f(x) = x3 , so f(a) = f(64). Differentials Linear Approximation Formula.
From www.youtube.com
Calc I Lesson 15 Linear Approximations and Differentials YouTube Differentials Linear Approximation Formula Describe the linear approximation to a function at a point. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Write the linearization of a given function. Use the tangent plane to approximate a function of two variables at a point. Draw a graph that illustrates the use of. Differentials Linear Approximation Formula.
From www.slideserve.com
PPT 6.6—Differentials Linear Approximation PowerPoint Presentation Differentials Linear Approximation Formula As long as the change dx in input x is. Use the tangent plane to approximate a function of two variables at a point. A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. Draw a graph that illustrates the use of differentials to approximate the change in a. Write the. Differentials Linear Approximation Formula.
From www.slideshare.net
Lesson 12 Linear Approximation Differentials Linear Approximation Formula A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy =. Draw a graph that illustrates the use of differentials to approximate the change in a. Draw a graph that illustrates. Differentials Linear Approximation Formula.
From www.pinterest.com
Linear Approximation and Differentials in Calculus Linear function Differentials Linear Approximation Formula Determine the equation of a plane tangent to a given surface at a point. Draw a graph that illustrates the use of differentials to approximate the change in a. 4.2.1 describe the linear approximation to a function at a point. Use the tangent plane to approximate a function of two variables at a point. The resulting linear approximation of the. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula Draw a graph that illustrates the use of differentials to approximate the change in a. Describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the change in a. As long as the change dx in input x is. Describe the linear approximation to a function at a point.. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula Write the linearization of a given function. Draw a graph that illustrates the use of differentials to approximate the change in a. The basic formula for linear approximation is: Write the linearization of a given function. Describe the linear approximation to a function at a point. Draw a graph that illustrates the use of differentials to approximate the change in. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula Draw a graph that illustrates the use of differentials to approximate the change in a. F(x) = f(a) ' + f (a)(x − a) here. The basic formula for linear approximation is: Differentials are useful when the value of a quantity is unimportant, only the approximate change in the quantity in response to a change in input is desired. Write. Differentials Linear Approximation Formula.
From owlcation.com
Linear Approximation and Differentials in Calculus Owlcation Differentials Linear Approximation Formula The basic formula for linear approximation is: A = 64 and f(x) = x3 , so f(a) = f(64) = 4 and f '(a) = 1. Determine the equation of a plane tangent to a given surface at a point. The resulting linear approximation of the change in the \(y\) value is called the differential \(dy\text{,}\) given by \begin{equation*} dy. Differentials Linear Approximation Formula.