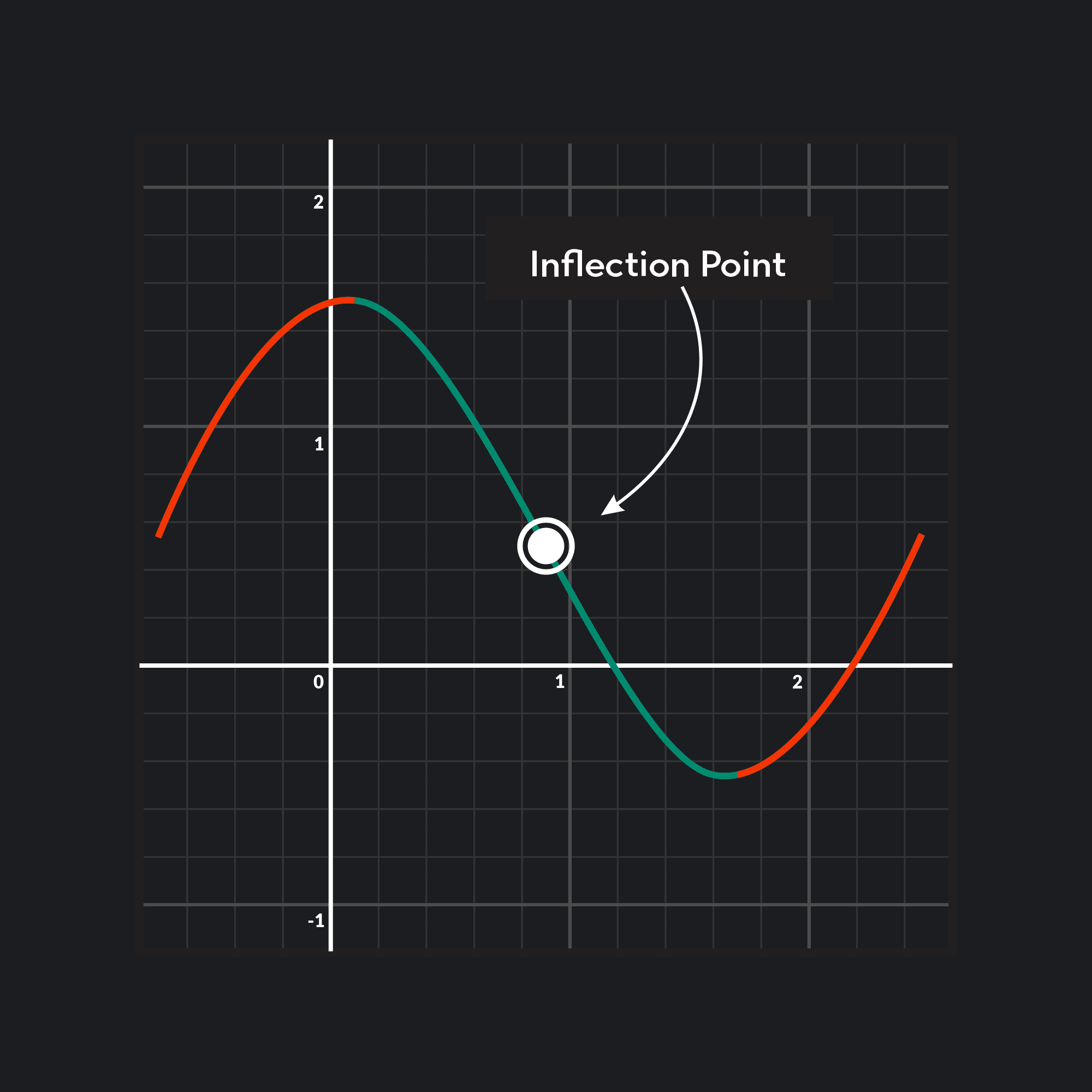
Point Of Inflection Difference Horizontal at Ernest Attaway blog

Point Of Inflection Difference Horizontal. This means that a point of inflection is a point. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. In principle, it's very straightforward: In this article, the concept and meaning of. When the second derivative is negative, the function is concave downward. A horizontal point of inflection is where the tangent line is horizontal. The derivative or slope here is zero, because the tangent line is flat. To find the points of inflection you simply find the points where f''(x) = 0 (and if you're being careful, check that f'' actually changes sign. And the inflection point is where it goes from concave upward to concave downward (or vice versa). A point of inflection is a point on the graph of where the function changes from concave up to concave down, or vice versa. A point of inflection is any point at which a curve changes from being convex to being concave.

A point of inflection is any point at which a curve changes from being convex to being concave. To find the points of inflection you simply find the points where f''(x) = 0 (and if you're being careful, check that f'' actually changes sign. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. In principle, it's very straightforward: The derivative or slope here is zero, because the tangent line is flat. In this article, the concept and meaning of. A point of inflection is a point on the graph of where the function changes from concave up to concave down, or vice versa. A horizontal point of inflection is where the tangent line is horizontal. When the second derivative is negative, the function is concave downward. This means that a point of inflection is a point.

Inflection Point Definition and How to Find It in 5 Steps Outlier

Point Of Inflection Difference Horizontal The derivative or slope here is zero, because the tangent line is flat. In this article, the concept and meaning of. And the inflection point is where it goes from concave upward to concave downward (or vice versa). To find the points of inflection you simply find the points where f''(x) = 0 (and if you're being careful, check that f'' actually changes sign. In principle, it's very straightforward: This means that a point of inflection is a point. A point of inflection is any point at which a curve changes from being convex to being concave. A horizontal point of inflection is where the tangent line is horizontal. When the second derivative is negative, the function is concave downward. A point of inflection is a point on the graph of where the function changes from concave up to concave down, or vice versa. The point where the function is neither concave nor convex is known as inflection point or the point of inflection. The derivative or slope here is zero, because the tangent line is flat.