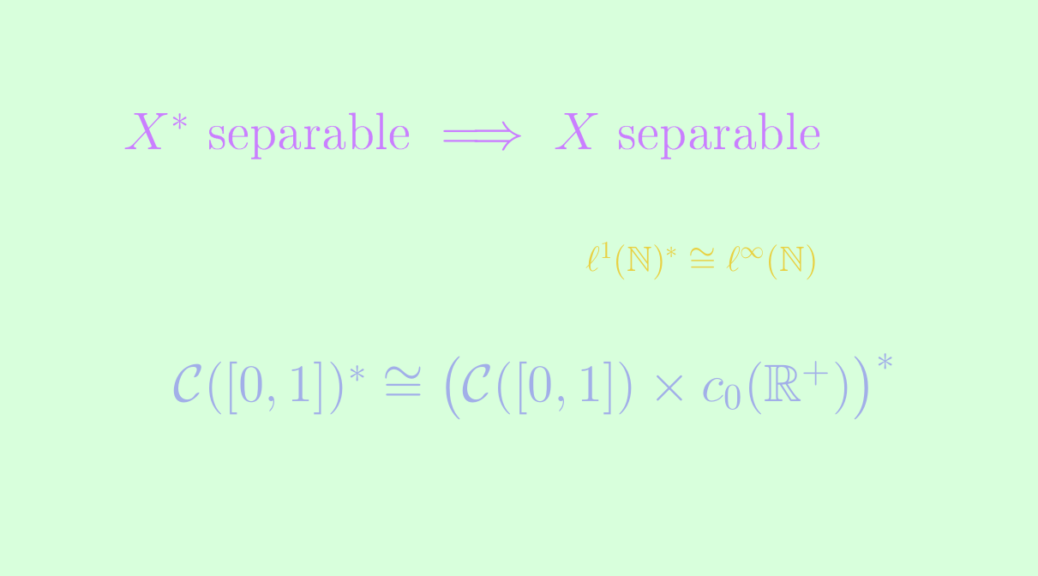Math Counterexample . Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false A counterexample is a form of counter proof. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. Counterexamples are indispensable in mathematics for several reasons: A counterexample is a specific case or instance that disproves a conjecture or statement. A counterexample is an example that disproves a conjecture. If even one counterexample exists, it means the conjecture is not universally true. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. How do you make a. Suppose you were given a mathematical pattern like \(h =.
from www.mathcounterexamples.net
A counterexample is an example that disproves a conjecture. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is a specific case or instance that disproves a conjecture or statement. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. Suppose you were given a mathematical pattern like \(h =. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. How do you make a. A counterexample is a form of counter proof. If even one counterexample exists, it means the conjecture is not universally true. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false
Separability of a vector space and its dual Math Counterexamples
Math Counterexample Counterexamples are indispensable in mathematics for several reasons: How do you make a. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is an example that disproves a conjecture. If even one counterexample exists, it means the conjecture is not universally true. Suppose you were given a mathematical pattern like \(h =. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. A counterexample is a form of counter proof. Counterexamples are indispensable in mathematics for several reasons: Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false A counterexample is a specific case or instance that disproves a conjecture or statement.
From www.youtube.com
Counterexample in Discrete Mathematics with Example YouTube Math Counterexample If even one counterexample exists, it means the conjecture is not universally true. A counterexample is a specific case or instance that disproves a conjecture or statement. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p. Math Counterexample.
From www.slideshare.net
Dec.10 Counterexamples Math Counterexample Counterexamples are indispensable in mathematics for several reasons: A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. How do you make a. A counterexample is a form of counter proof. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion.. Math Counterexample.
From www.slideshare.net
Dec.10 Counterexamples Math Counterexample How do you make a. If even one counterexample exists, it means the conjecture is not universally true. A counterexample is an example that disproves a conjecture. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is an example that meets the mathematical statement's condition but does. Math Counterexample.
From www.youtube.com
Proof by Counterexample YouTube Math Counterexample Counterexamples are indispensable in mathematics for several reasons: How do you make a. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is a specific case or instance that disproves a conjecture or statement. Suppose you were given a mathematical pattern like \(h =. Relative to the. Math Counterexample.
From www.slideshare.net
Dec.10 Counterexamples Math Counterexample A counterexample is an example that disproves a conjecture. If even one counterexample exists, it means the conjecture is not universally true. A counterexample is a specific case or instance that disproves a conjecture or statement. Counterexamples are indispensable in mathematics for several reasons: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c. Math Counterexample.
From www.mathcounterexamples.net
counterexamplearoundinfiniteproductsimage Math Counterexamples Math Counterexample A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. Suppose you were given a mathematical pattern like \(h =. A counterexample is a form of counter proof. A counterexample is a specific case or instance that disproves a conjecture or statement. If even one counterexample exists, it means the. Math Counterexample.
From slideplayer.com
Inductive Reasoning Inductive Reasoning is the process of forming a conjecture based on a set Math Counterexample A counterexample is an example that disproves a conjecture. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such. Math Counterexample.
From www.slideserve.com
PPT Math 12 Warmup PowerPoint Presentation, free download ID2974686 Math Counterexample A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. Counterexamples are indispensable in mathematics for several reasons: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p. Math Counterexample.
From www.youtube.com
Proof by Smallest Counterexample YouTube Math Counterexample A counterexample is an example that disproves a conjecture. A counterexample is a specific case or instance that disproves a conjecture or statement. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's. Math Counterexample.
From calcworkshop.com
Direct Proof (Explained w/ 11+ StepbyStep Examples!) Math Counterexample A counterexample is an example that disproves a conjecture. If even one counterexample exists, it means the conjecture is not universally true. Suppose you were given a mathematical pattern like \(h =. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. How do you make a. A counterexample is an. Math Counterexample.
From study.com
Counterexample in Mathematics Definition, Proofs & Examples Lesson Math Counterexample A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. A counterexample is an example that disproves a conjecture. Suppose you were given a mathematical pattern like \(h =. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample. Math Counterexample.
From www.slideserve.com
PPT Section One PowerPoint Presentation, free download ID6364513 Math Counterexample A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. A counterexample is an example that disproves a conjecture. A counterexample is a form of counter proof. If even one counterexample. Math Counterexample.
From study.com
Quiz & Worksheet Counterexamples in Math Math Counterexample How do you make a. A counterexample is a specific case or instance that disproves a conjecture or statement. Counterexamples are indispensable in mathematics for several reasons: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false A counterexample is an example that meets the mathematical statement's condition but does. Math Counterexample.
From www.youtube.com
2.1 Example 4 Find a counterexample YouTube Math Counterexample If even one counterexample exists, it means the conjecture is not universally true. How do you make a. Suppose you were given a mathematical pattern like \(h =. Counterexamples are indispensable in mathematics for several reasons: A counterexample is a form of counter proof. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions. Math Counterexample.
From www.studocu.com
Mathematics in the Modern World Quiz in Finding Counterexample Studocu Math Counterexample How do you make a. If even one counterexample exists, it means the conjecture is not universally true. A counterexample is an example that disproves a conjecture. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false A counterexample is a form of counter proof. Counterexamples are indispensable in mathematics. Math Counterexample.
From www.mathcounterexamples.net
Math Counterexamples Mathematical exceptions to the rules or intuition Math Counterexample A counterexample is an example that disproves a conjecture. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. Suppose you were given a mathematical pattern like \(h =. Counterexamples are indispensable in mathematics for several reasons: How do you make a. Relative to the logical implication \(p \rightarrow q\text{,}\) a. Math Counterexample.
From www.youtube.com
Counterexamples Worked example Praxis Core Math Khan Academy YouTube Math Counterexample A counterexample is a form of counter proof. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. Counterexamples are indispensable in mathematics for several reasons: A counterexample is a specific. Math Counterexample.
From www.slideserve.com
PPT Tools of Geometry PowerPoint Presentation, free download ID2263780 Math Counterexample A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. Suppose you were given a mathematical pattern like \(h =. A counterexample is a specific case or instance that disproves a. Math Counterexample.
From www.youtube.com
Conjectures and Counterexamples Examples (Basic Geometry Concepts) YouTube Math Counterexample Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. A counterexample is an example that disproves a conjecture. Suppose you were given a mathematical pattern like \(h =. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample. Math Counterexample.
From www.slideserve.com
PPT Logical equivalence PowerPoint Presentation, free download ID5404570 Math Counterexample A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. Suppose you were given a mathematical pattern like \(h =. A counterexample is a form of counter proof. Counterexamples are indispensable in mathematics for several reasons: A counterexample is an example that disproves a conjecture. Relative to the logical implication \(p. Math Counterexample.
From www.researchgate.net
Examples of the three types of counterexamples Download Table Math Counterexample A counterexample is a form of counter proof. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. How do you make a. If even one counterexample exists, it means the conjecture. Math Counterexample.
From sites.psu.edu
Counterexample Functions in Math My Path to Learning Math Counterexample Suppose you were given a mathematical pattern like \(h =. Counterexamples are indispensable in mathematics for several reasons: A counterexample is a specific case or instance that disproves a conjecture or statement. How do you make a. If even one counterexample exists, it means the conjecture is not universally true. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement. Math Counterexample.
From slideplayer.com
Direct Proof and Counterexample I ppt download Math Counterexample Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Counterexamples are indispensable in mathematics for several reasons: A counterexample is a form of counter proof. Suppose you were given a mathematical pattern like \(h =. If even one counterexample exists, it means the conjecture is not universally true. Given. Math Counterexample.
From www.studocu.com
Intro To Discrete Math Proof by Smallest Counterexample Proof by smallest counterexample Math Counterexample A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false A. Math Counterexample.
From www.slideserve.com
PPT Discrete Maths PowerPoint Presentation, free download ID1967699 Math Counterexample A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. A counterexample is a specific case or instance that disproves a conjecture or statement. Counterexamples are indispensable in mathematics for several reasons: Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is. Math Counterexample.
From www.cuemath.com
Counterexample Cuemath Math Counterexample If even one counterexample exists, it means the conjecture is not universally true. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is a specific case or instance that disproves a conjecture or statement. A counterexample is a form of counter proof. Counterexamples are indispensable in mathematics. Math Counterexample.
From www.mathcounterexamples.net
Math Counterexamples Mathematical exceptions to the rules or intuition Math Counterexample If even one counterexample exists, it means the conjecture is not universally true. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false A counterexample is an example that disproves a conjecture. Counterexamples are indispensable in mathematics for several reasons: A counterexample is a specific case or instance that disproves. Math Counterexample.
From www.youtube.com
Proof & counterexamples YouTube Math Counterexample Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false A counterexample is a form of counter proof. A counterexample is a specific case or instance that disproves a conjecture or statement. Counterexamples are indispensable in mathematics for several reasons: A counterexample is an example that disproves a conjecture. If. Math Counterexample.
From www.youtube.com
Conjectures and Counterexamples Lesson (Basic Geometry Concepts) YouTube Math Counterexample A counterexample is a form of counter proof. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is an example that disproves a conjecture. How do you make a. Counterexamples are indispensable in mathematics for several reasons: A counterexample is an example that meets the mathematical statement's. Math Counterexample.
From study.com
How to Identify Counterexamples in Algebra Algebra Math Counterexample A counterexample is a specific case or instance that disproves a conjecture or statement. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. A counterexample is an example that disproves a. Math Counterexample.
From www.mathcounterexamples.net
counterexamplearoundmoreratheoremimage Math Counterexamples Math Counterexample A counterexample is a form of counter proof. A counterexample is a specific case or instance that disproves a conjecture or statement. A counterexample is an example that meets the mathematical statement's condition but does not lead to the statement's conclusion. A counterexample is an example that disproves a conjecture. A counterexample is an example that disproves a statement, proposition,. Math Counterexample.
From www.youtube.com
Proof by Counterexample YouTube Math Counterexample Suppose you were given a mathematical pattern like \(h =. How do you make a. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false If even one counterexample exists, it. Math Counterexample.
From www.mathcounterexamples.net
Separability of a vector space and its dual Math Counterexamples Math Counterexample Suppose you were given a mathematical pattern like \(h =. Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false If even one counterexample exists, it means the conjecture is not universally true. Given a hypothesis stating that f(x) is true for all x in s, show that there exists. Math Counterexample.
From www.showme.com
Geom Sem1 Final Review p4 1 Math, geometry, Counterexample ShowMe Math Counterexample Counterexamples are indispensable in mathematics for several reasons: Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b. A counterexample is an example that disproves a statement, proposition, or theorem by satisfying the conditions but contradicting the conclusion. A counterexample is an example that meets the mathematical statement's condition but does. Math Counterexample.
From www.mathcounterexamples.net
Mean independent and correlated variables Math Counterexamples Math Counterexample Relative to the logical implication \(p \rightarrow q\text{,}\) a statement \(c\) such that \(p \land c \rightarrow q\) is false Counterexamples are indispensable in mathematics for several reasons: If even one counterexample exists, it means the conjecture is not universally true. Given a hypothesis stating that f(x) is true for all x in s, show that there exists a b.. Math Counterexample.