Low Pass Filter Z Domain . As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of.
from www.cs.princeton.edu
As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient.
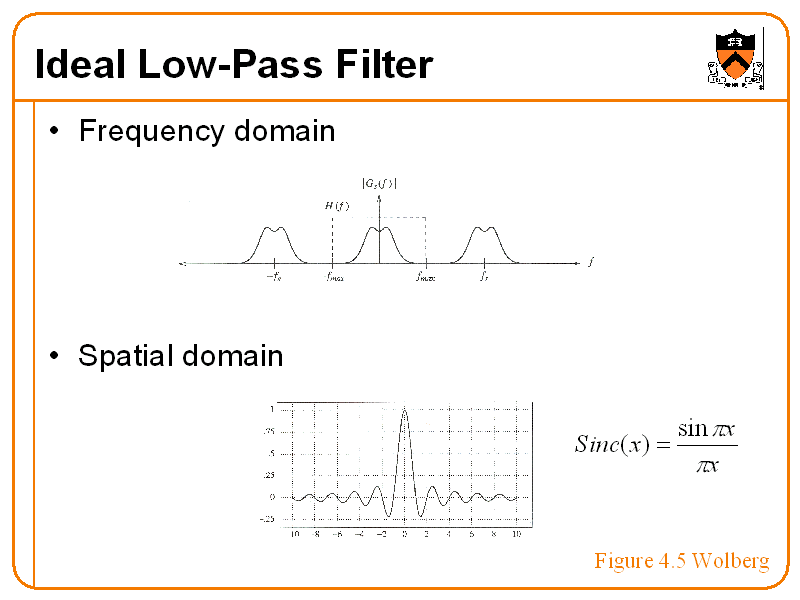
Ideal LowPass Filter
Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described in chapter 19, recursive filters are.
From mungfali.com
Low Pass Filter Plot Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From www.researchgate.net
Lowpass filter responses in the frequency domain with varying Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described in chapter 19, recursive filters are. In the time domain, we just convolve x k. Low Pass Filter Z Domain.
From www.slideshare.net
Implementation and comparison of Low pass filters in Frequency domain Low Pass Filter Z Domain As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From electronics.stackexchange.com
microcontroller How to amplify the output of a digital low pass Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. In the time domain, we just convolve x k with the inverse fourier transform of. As described. Low Pass Filter Z Domain.
From www.youtube.com
Lowpass and Highpass Filters (Explanation and Examples) YouTube Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From x-engineer.org
What is a low pass filter used for ? Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From www.youtube.com
Low pass filter simulation in LTSpice YouTube Low Pass Filter Z Domain As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From mavink.com
Passive Low Pass Filter Design Low Pass Filter Z Domain As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k. Low Pass Filter Z Domain.
From www.circuitdiagram.co
low pass filter circuit diagram Circuit Diagram Low Pass Filter Z Domain As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From www.researchgate.net
The four common filters. (a) Lowpass filter, passes signals with a Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From mungfali.com
Active Low Pass Filter Design Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From www.engineeringradio.us
Low Pass Filter design Engineering Radio Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. As described. Low Pass Filter Z Domain.
From www.reddit.com
Understanding ZDomain r/ControlTheory Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From circuitdiagramcentre.blogspot.com
How to Make a Simple Active Low Pass Filter Circuit Using IC 741 Low Pass Filter Z Domain As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From www.cs.princeton.edu
Ideal LowPass Filter Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From manualdiagramausterlitz.z19.web.core.windows.net
Low Pass Filter Schematic Symbol Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From electronics.stackexchange.com
c How can I design a low pass filter using Z transform in Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described. Low Pass Filter Z Domain.
From flylib.com
THE ZTRANSFORM Chapter Six. Infinite Impulse Response Filters Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. In the time domain, we just convolve x k. Low Pass Filter Z Domain.
From pdfprof.com
discrete low pass filter z transform Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described. Low Pass Filter Z Domain.
From www.youtube.com
Basic FIR Filters and the zTransform YouTube Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described in chapter 19, recursive filters are. In the time domain, we just convolve x k. Low Pass Filter Z Domain.
From www.circuitdiagram.co
circuit diagram of low pass filter Circuit Diagram Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From circuitdatasandoval.z4.web.core.windows.net
Active And Passive Low Pass Filter Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described. Low Pass Filter Z Domain.
From www.researchgate.net
(a) Current mode lowpass filter generated from Figure 4(b) and using a Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From legendtechz.blogspot.com
35. Explain about Ideal Low Pass Filter (ILPF) in frequency domain Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described. Low Pass Filter Z Domain.
From www.youtube.com
RC LowPass Filter (TimeDomain and FrequencyDomain Explained) YouTube Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From www.youtube.com
First Order Low Pass Filter Design And Scaling(हिन्दी ) YouTube Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In the time domain, we just convolve x k with the inverse fourier transform of. As described. Low Pass Filter Z Domain.
From www.slideserve.com
PPT Lecture 15 ContinuousTime Transfer Functions PowerPoint Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described. Low Pass Filter Z Domain.
From www.youtube.com
Analog Low Pass Filter and Simulation in Multisim Part 1/4 YouTube Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From www.allaboutcircuits.com
What Is a Low Pass Filter? A Tutorial on the Basics of Passive RC Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described. Low Pass Filter Z Domain.
From www.electricity-magnetism.org
LowPass Filters How it works, Application & Advantages Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From mavink.com
What Is A Low Pass Filter Low Pass Filter Z Domain In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From www.edn.com
Digital Lowpass A filter by any other name is still a filter EDN Low Pass Filter Z Domain As already mentioned, we can apply the effects of the filter in either the time domain or the frequency domain. As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous. Low Pass Filter Z Domain.
From www.youtube.com
LTspice tutorial 27 Low pass filter ac analysis circuit design YouTube Low Pass Filter Z Domain As described in chapter 19, recursive filters are. In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From www.mathforengineers.com
Low Pass Filter Transfer Function Low Pass Filter Z Domain As described in chapter 19, recursive filters are. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. In the time domain, we just convolve x k with the inverse fourier transform of. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.
From www.youtube.com
Lowpass filter basics YouTube Low Pass Filter Z Domain In the time domain, we just convolve x k with the inverse fourier transform of. In this short tutorial, we will derive the relationship between the corner frequency omega in the continuous time domain and the a coefficient. As described in chapter 19, recursive filters are. As already mentioned, we can apply the effects of the filter in either the. Low Pass Filter Z Domain.